名校
1 . 已知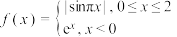 ,若存在实数
,若存在实数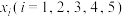 ,当
,当 时,满足
时,满足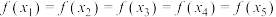 ,则
,则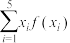 的取值范围为
的取值范围为__________ .
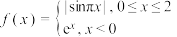 ,若存在实数
,若存在实数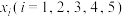 ,当
,当 时,满足
时,满足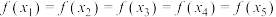 ,则
,则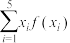 的取值范围为
的取值范围为
您最近半年使用:0次
名校
2 . 已知函数 ,关于
,关于 的方程
的方程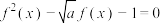 有以下结论:
有以下结论:
①当 时,方程
时,方程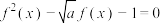 恒有根;
恒有根;
②当 时,方程
时,方程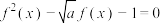 在
在 内最多有9个不等实根;
内最多有9个不等实根;
③当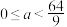 时,方程
时,方程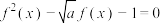 在
在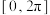 内有两个不等实根;
内有两个不等实根;
④若方程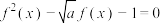 在
在 内根的个数为正偶数,则所有根之和为
内根的个数为正偶数,则所有根之和为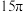 .
.
其中正确的结论是_________ (填写所有正确结论的编号).
 ,关于
,关于 的方程
的方程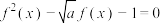 有以下结论:
有以下结论:①当
 时,方程
时,方程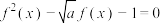 恒有根;
恒有根;②当
 时,方程
时,方程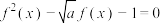 在
在 内最多有9个不等实根;
内最多有9个不等实根;③当
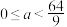 时,方程
时,方程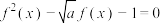 在
在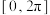 内有两个不等实根;
内有两个不等实根;④若方程
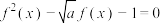 在
在 内根的个数为正偶数,则所有根之和为
内根的个数为正偶数,则所有根之和为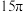 .
.其中正确的结论是
您最近半年使用:0次
名校
3 . 设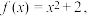 ,
,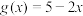 ,用
,用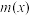 表示
表示 ,
, 中较小者,记为
中较小者,记为 ,若方程
,若方程 恰有
恰有 三个不同的实数解,则实数
三个不同的实数解,则实数 的取值范围为
的取值范围为______ .
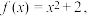 ,
,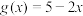 ,用
,用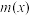 表示
表示 ,
, 中较小者,记为
中较小者,记为 ,若方程
,若方程 恰有
恰有 三个不同的实数解,则实数
三个不同的实数解,则实数 的取值范围为
的取值范围为
您最近半年使用:0次
解题方法
4 . 若函数 有两个零点,则实数
有两个零点,则实数 的取值范围是
的取值范围是__________ .
 有两个零点,则实数
有两个零点,则实数 的取值范围是
的取值范围是
您最近半年使用:0次
5 . 已知正方形 的四个顶点均在函数
的四个顶点均在函数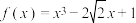 的图象上,若
的图象上,若 两点的横坐标分别为
两点的横坐标分别为 ,则
,则
________ .
 的四个顶点均在函数
的四个顶点均在函数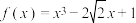 的图象上,若
的图象上,若 两点的横坐标分别为
两点的横坐标分别为 ,则
,则
您最近半年使用:0次
2024·全国·模拟预测
6 . 已知函数 的图象与直线
的图象与直线 的交点的横坐标分别为
的交点的横坐标分别为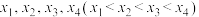 ,则( )
,则( )
 的图象与直线
的图象与直线 的交点的横坐标分别为
的交点的横坐标分别为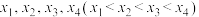 ,则( )
,则( )A. | B. |
C.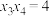 | D. 的最小值为 的最小值为 |
您最近半年使用:0次
名校
解题方法
7 . 设实系数一元二次方程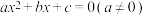 ①,有两根
①,有两根 ,
,
则方程可变形为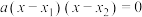 ,展开得
,展开得 ②,
②,
比较①②可以得到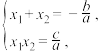
这表明,任何一个一元二次方程的根与系数的关系为:两个根的和等于一次项系数与二次项系数的比的相反数,两个根的积等于常数项与二次项系数的比.这就是我们熟知的一元二次方程的韦达定理.
事实上,与二次方程类似,一元三次方程也有韦达定理.
设方程 有三个根
有三个根 ,则有
,则有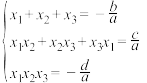 ③
③
(1)证明公式③,即一元三次方程的韦达定理;
(2)已知函数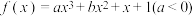 恰有两个零点.
恰有两个零点.
(i)求证: 的其中一个零点大于0,另一个零点大于
的其中一个零点大于0,另一个零点大于 且小于0;
且小于0;
(ii)求 的取值范围.
的取值范围.
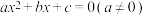 ①,有两根
①,有两根 ,
,则方程可变形为
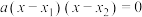 ,展开得
,展开得 ②,
②,比较①②可以得到
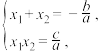
这表明,任何一个一元二次方程的根与系数的关系为:两个根的和等于一次项系数与二次项系数的比的相反数,两个根的积等于常数项与二次项系数的比.这就是我们熟知的一元二次方程的韦达定理.
事实上,与二次方程类似,一元三次方程也有韦达定理.
设方程
 有三个根
有三个根 ,则有
,则有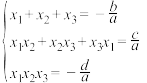 ③
③(1)证明公式③,即一元三次方程的韦达定理;
(2)已知函数
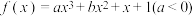 恰有两个零点.
恰有两个零点.(i)求证:
 的其中一个零点大于0,另一个零点大于
的其中一个零点大于0,另一个零点大于 且小于0;
且小于0;(ii)求
 的取值范围.
的取值范围.
您最近半年使用:0次
8 . 已知函数 的最大值为1.
的最大值为1.
(1)求实数 的值;
的值;
(2)若函数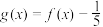 在区间
在区间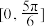 上有两个零点
上有两个零点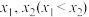 ,求
,求 的值.
的值.
 的最大值为1.
的最大值为1.(1)求实数
 的值;
的值;(2)若函数
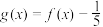 在区间
在区间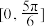 上有两个零点
上有两个零点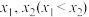 ,求
,求 的值.
的值.
您最近半年使用:0次
名校
9 . 设方程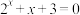 和方程
和方程 的根分别为
的根分别为 ,设函数
,设函数 ,则( )
,则( )
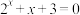 和方程
和方程 的根分别为
的根分别为 ,设函数
,设函数 ,则( )
,则( )A.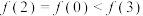 | B.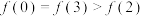 |
C.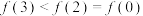 | D.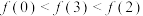 |
您最近半年使用:0次
解题方法
10 . 三个函数 ,
, ,
,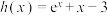 的零点分别为
的零点分别为 ,则
,则 之间的大小关系为( )
之间的大小关系为( )
 ,
, ,
,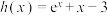 的零点分别为
的零点分别为 ,则
,则 之间的大小关系为( )
之间的大小关系为( )A.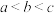 | B. |
C. | D.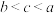 |
您最近半年使用:0次



