名校
解题方法
1 . 瑞士数学家欧拉于1748年提出了著名的公式: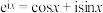 ,其中
,其中 是自然对数的底数,
是自然对数的底数, 是虚数单位,该公式被称为欧拉公式.根据欧拉公式,下列选项正确的是( )
是虚数单位,该公式被称为欧拉公式.根据欧拉公式,下列选项正确的是( )
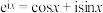 ,其中
,其中 是自然对数的底数,
是自然对数的底数, 是虚数单位,该公式被称为欧拉公式.根据欧拉公式,下列选项正确的是( )
是虚数单位,该公式被称为欧拉公式.根据欧拉公式,下列选项正确的是( )A.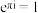 |
B.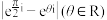 的最大值为2 的最大值为2 |
C.复数 在复平面内对应的点位于第二象限 在复平面内对应的点位于第二象限 |
D.若 , , 在复平面内分别对应点 在复平面内分别对应点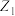 , ,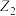 ,则 ,则 面积的最大值为 面积的最大值为 |
您最近一年使用:0次
2024-04-20更新
|
963次组卷
|
4卷引用:广东省广州市第八十六中学2021-2022学年高一下学期期末数学试题
2024·内蒙古赤峰·模拟预测
解题方法
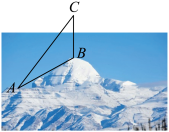
2 . 为了测量西藏被誉称为“阿里之巅”冈仁波齐山峰的高度,通常采用人工攀登的方式进行,测量人员从山脚开始,直到到达山顶分段测量过程中,已知竖立在 点处的测量觇标高
点处的测量觇标高 米,攀登者们在
米,攀登者们在 处测得,到觇标底点
处测得,到觇标底点 和顶点
和顶点 的仰角分别为
的仰角分别为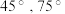 ,则
,则 的高度差约为( )
的高度差约为( )
 点处的测量觇标高
点处的测量觇标高 米,攀登者们在
米,攀登者们在 处测得,到觇标底点
处测得,到觇标底点 和顶点
和顶点 的仰角分别为
的仰角分别为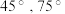 ,则
,则 的高度差约为( )
的高度差约为( )
| A.7.32米 | B.7.07米 | C.27.32米 | D.30米 |
您最近一年使用:0次
2024-03-16更新
|
619次组卷
|
5卷引用:6.4.3 第3课时 余弦定理、正弦定理应用举例【第二课】“上好三节课,做好三套题“高中数学素养晋级之路
(已下线)6.4.3 第3课时 余弦定理、正弦定理应用举例【第二课】“上好三节课,做好三套题“高中数学素养晋级之路(已下线)6.4.3 第3课时 余弦定理、正弦定理应用举例【第三练】“上好三节课,做好三套题“高中数学素养晋级之路内蒙古赤峰市2023~2024学年高三上学期1.30模拟文科数学试题内蒙古赤峰市2024届高三上学期1.30模拟理科数学试题(已下线)专题3 最佳视角 米勒定理【练】
23-24高三上·贵州贵阳·阶段练习
名校
解题方法
3 . 秦九韶(1208年~1268年),字道古,祖籍鲁郡(今河南省范县),出生于普州(今四川安岳县).南宋著名数学家,与李冶、杨辉、朱世杰并称宋元数学四大家.1247年秦九韶完成了著作《数书九章》,其中的大衍求一术(一次同余方程组问题的解法,也就是现在所称的中国剩余定理)、三斜求积术和秦九韶算法(高次方程正根的数值求法)是有世界意义的重要贡献.设 的三个内角
的三个内角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,面积为
,面积为 ,秦九韶提出的“三斜求积术”公式为
,秦九韶提出的“三斜求积术”公式为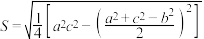 ,若
,若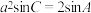 ,
,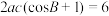 ,则由“三斜求积术”公式可得
,则由“三斜求积术”公式可得 的面积为( )
的面积为( )
 的三个内角
的三个内角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,面积为
,面积为 ,秦九韶提出的“三斜求积术”公式为
,秦九韶提出的“三斜求积术”公式为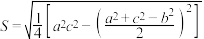 ,若
,若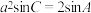 ,
,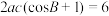 ,则由“三斜求积术”公式可得
,则由“三斜求积术”公式可得 的面积为( )
的面积为( )A. | B. | C. | D.1 |
您最近一年使用:0次
2024-01-31更新
|
574次组卷
|
6卷引用:第11章 解三角形 单元综合检测(重点)-《重难点题型·高分突破》(苏教版2019必修第二册)
(已下线)第11章 解三角形 单元综合检测(重点)-《重难点题型·高分突破》(苏教版2019必修第二册)广东省佛山市南海区桂华中学2023-2024学年高一下学期第一次阶段测试数学试卷贵州省贵阳市第一中学2024届高三上学期高考适应性月考卷(五)数学试题(已下线)考点20 三角函数的数学文化 --2024届高考数学考点总动员【讲】(已下线)思想02 运用数形结合的思想方法解题(4大核心考点)(讲义)(已下线)专题1 三斜求积 巧求面积 练
4 . “三斜求积术”是我国宋代的数学家秦九韶用实例的形式提出的,其实质是根据三角形的三边长 求三角形面积
求三角形面积 ,即
,即 .现有面积为
.现有面积为 的
的 满足
满足 ,则
,则 的周长是( )
的周长是( )
 求三角形面积
求三角形面积 ,即
,即 .现有面积为
.现有面积为 的
的 满足
满足 ,则
,则 的周长是( )
的周长是( )| A.9 | B.12 | C.18 | D.36 |
您最近一年使用:0次
2024-01-20更新
|
679次组卷
|
9卷引用:专题10 余弦定理 正弦定理-《重难点题型·高分突破》(苏教版2019必修第二册)
(已下线)专题10 余弦定理 正弦定理-《重难点题型·高分突破》(苏教版2019必修第二册)(已下线)专题08 余弦定理 正弦定理(1)-《重难点题型·高分突破》(人教A版2019必修第二册)(已下线)6.4.3.2?正弦定理15种常考题型归类(2)-高频考点通关与解题策略(人教A版2019必修第二册)河南省郑州市基石中学2023-2024学年高一下学期4月月考数学试题(已下线)6.4.3.2 正弦定理——课后作业(提升版)北京市昌平区2024届高三上学期期末质量抽测数学试题(已下线)考点20 三角函数的数学文化 --2024届高考数学考点总动员【练】(已下线)压轴题平面向量与解三角形新定义题(九省联考第19题模式)练(已下线)专题1 三斜求积 巧求面积 练
名校
解题方法
5 . 数学家欧拉在1765年发现了九点圆,即在任意的三角形中,三边的中点、三条高的垂足、三条高的交点(垂心)与三角形顶点连线的中点,这九个点共圆,因此九点圆也称作欧拉圆.已知在 中,
中,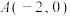 ,
, ,
,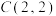 ,则
,则 的九点圆的半径为( )
的九点圆的半径为( )
 中,
中,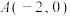 ,
, ,
,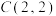 ,则
,则 的九点圆的半径为( )
的九点圆的半径为( )A.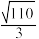 | B.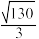 | C.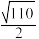 | D.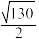 |
您最近一年使用:0次
2024-01-16更新
|
365次组卷
|
3卷引用:黑龙江省牡丹江市第一高级中学2023-2024学年高一下学期4月月考数学试题
黑龙江省牡丹江市第一高级中学2023-2024学年高一下学期4月月考数学试题广东省揭阳市2024届高三上学期期末教学质量测试数学试题(已下线)考点20 三角函数的数学文化 --2024届高考数学考点总动员【讲】
23-24高二上·辽宁葫芦岛·期末
6 . 我国辽代著名的前卫斜塔(又名瑞州古塔)位于葫芦岛市绥中县.现存塔身已经倾斜且与地面夹角60°,若将塔身看做直线,从塔的第三层地面到第三层顶可看做线段,且在地面的射影为1m,则该塔第三层地面到第三层顶的距离是( )
A.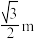 | B.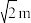 | C.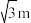 | D.2m |
您最近一年使用:0次
23-24高三上·重庆·阶段练习
名校
7 . 纳斯卡线条是一种巨型的地上绘图,位于秘鲁南部的纳斯卡荒原上,是存在了2000年的谜局:究竟是谁创造了它们并且为了什么而创造,至今仍无人能解,因此被列入“十大谜团”,在这些图案中,有一只身长50米的大蜘蛛(如图),现用视角为 的摄像头(注:当摄像头和所拍摄的圆形区域构成一个圆锥时,该圆锥的轴截面的顶角称为该摄像头的视角)在该蜘蛛图案的上方拍摄,使得整个蜘蛛图案落在边长为50米的正方形区域内,则该摄像头距地面的高度的最小值是( )
的摄像头(注:当摄像头和所拍摄的圆形区域构成一个圆锥时,该圆锥的轴截面的顶角称为该摄像头的视角)在该蜘蛛图案的上方拍摄,使得整个蜘蛛图案落在边长为50米的正方形区域内,则该摄像头距地面的高度的最小值是( )
 的摄像头(注:当摄像头和所拍摄的圆形区域构成一个圆锥时,该圆锥的轴截面的顶角称为该摄像头的视角)在该蜘蛛图案的上方拍摄,使得整个蜘蛛图案落在边长为50米的正方形区域内,则该摄像头距地面的高度的最小值是( )
的摄像头(注:当摄像头和所拍摄的圆形区域构成一个圆锥时,该圆锥的轴截面的顶角称为该摄像头的视角)在该蜘蛛图案的上方拍摄,使得整个蜘蛛图案落在边长为50米的正方形区域内,则该摄像头距地面的高度的最小值是( )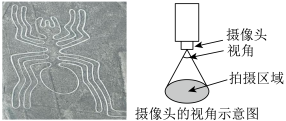
| A.50米 | B.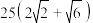 米 米 |
C.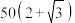 米 米 | D.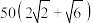 米 米 |
您最近一年使用:0次
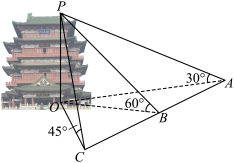
8 . 落霞与孤鹜齐飞,秋水共长天一色,滕王阁,江南三大名楼之一,因初唐诗人王勃所作《滕王阁序》而名传千古,如图所示,在滕王阁旁的水平地面上共线的三点A,B,C处测得其顶点P的仰角分别为30°,60°,45°,且AB=BC=75米,则滕王阁的高度OP=________ 米.
您最近一年使用:0次
2023-12-20更新
|
600次组卷
|
8卷引用:专题6.11 平面向量及其应用全章综合测试卷(基础篇)-举一反三系列
(已下线)专题6.11 平面向量及其应用全章综合测试卷(基础篇)-举一反三系列(已下线)6.4.3 课时3 余弦定理、正弦定理应用举例-高一数学同步精品课堂(人教A版2019必修第二册)(已下线)第11章 解三角形 章末题型归纳总结(1)-【帮课堂】(苏教版2019必修第二册)广西壮族自治区百色市德保县德保高中2023-2024学年高一下学期月考(一)(3月)数学试题(已下线)6.4.3.1 余弦定理——课后作业(巩固版)(已下线)6.4.3.1 余弦定理——课后作业(提升版)(已下线)第四章 三角函数与解三角形 第七节 解三角形应用举例(已下线)考点20 三角函数的数学文化 --2024届高考数学考点总动员【练】
23-24高三上·黑龙江哈尔滨·期中
名校
解题方法
9 . 南宋数学家秦九韶在《数书九章》中提出“三斜求积术”,即以小斜幂,并大斜幂,减中斜幂,余半之,自乘于上:以小斜幂乘大斜幂,减上,余四约之,为实:一为从隅,开平方得积,可用公式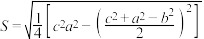 (其中a、b、c、S为三角形的三边和面积)表示.在
(其中a、b、c、S为三角形的三边和面积)表示.在 中,a、b、c分别为角A、B、C所对的边,若
中,a、b、c分别为角A、B、C所对的边,若 ,且
,且 ,则下列命题正确的是( )
,则下列命题正确的是( )
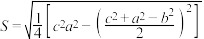 (其中a、b、c、S为三角形的三边和面积)表示.在
(其中a、b、c、S为三角形的三边和面积)表示.在 中,a、b、c分别为角A、B、C所对的边,若
中,a、b、c分别为角A、B、C所对的边,若 ,且
,且 ,则下列命题正确的是( )
,则下列命题正确的是( )A. 面积的最大值是 面积的最大值是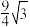 | B. |
C.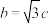 | D. 面积的最大值是 面积的最大值是 |
您最近一年使用:0次
2023·全国·模拟预测
解题方法
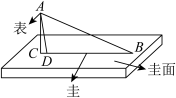
10 . 圭表是我国古代一种通过测量正午日影长度来推定节气的天文仪器,它包括一根呈南北方向的水平长尺(称为“圭”)和一根直立于圭面的标杆(称为“表”),如图.成语有云:“立竿见影”,《周髀算经》里记载的二十四节气就是通过圭表测量日影长度来确定的.利用圭表测得某市在每年夏至日的早上8:00和中午13:00的太阳高度角分别为 (
( )和
)和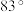 (
(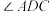 ).设表高
).设表高 为1米,则影差
为1米,则影差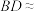 ( )(参考数据:
( )(参考数据: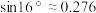 ,
,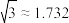 )
)
 (
( )和
)和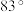 (
(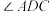 ).设表高
).设表高 为1米,则影差
为1米,则影差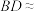 ( )(参考数据:
( )(参考数据: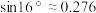 ,
,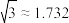 )
)
| A.2.016米 | B.2.232米 | C.2.428米 | D.2.614米 |
您最近一年使用:0次



