1 . 若圆C与抛物线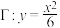 在公共点B处有相同的切线,且C与y轴切于
在公共点B处有相同的切线,且C与y轴切于 的焦点A,则
的焦点A,则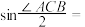
_________ .
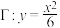 在公共点B处有相同的切线,且C与y轴切于
在公共点B处有相同的切线,且C与y轴切于 的焦点A,则
的焦点A,则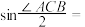
您最近半年使用:0次
名校
2 . 已知圆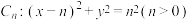 ,则下列结论正确的是( )
,则下列结论正确的是( )
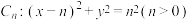 ,则下列结论正确的是( )
,则下列结论正确的是( )A.无论 为何值,圆 为何值,圆 都与 都与 轴相切 轴相切 |
B.存在整数 ,使得圆 ,使得圆 与直线 与直线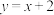 相切 相切 |
C.当 时,圆 时,圆 上恰有11个整点(横、纵坐标都是整数的点) 上恰有11个整点(横、纵坐标都是整数的点) |
D.若圆 上恰有两个点到直线 上恰有两个点到直线 的距离为 的距离为 ,则 ,则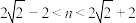 |
您最近半年使用:0次
2024-02-28更新
|
400次组卷
|
3卷引用:江西省南昌市第二中学等部分学校2024届高三下学期3月联考数学试题
名校
3 . 在平面直角坐标系 中,已知双曲线
中,已知双曲线 的右顶点为A,直线l与以O为圆心,
的右顶点为A,直线l与以O为圆心,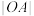 为半径的圆相切,切点为P.则( )
为半径的圆相切,切点为P.则( )
 中,已知双曲线
中,已知双曲线 的右顶点为A,直线l与以O为圆心,
的右顶点为A,直线l与以O为圆心,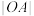 为半径的圆相切,切点为P.则( )
为半径的圆相切,切点为P.则( )A.双曲线C的离心率为 |
B.当直线 与双曲线C的一条渐近线重合时,直线l过双曲线C的一个焦点 与双曲线C的一条渐近线重合时,直线l过双曲线C的一个焦点 |
C.当直线l与双曲线C的一条渐近线平行吋,若直线l与双曲线C的交点为Q,则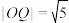 |
D.若直线l与双曲线C的两条渐近线分别交于D,E两点,与双曲线C分别交于M,N两点,则 |
您最近半年使用:0次
2024-02-18更新
|
271次组卷
|
3卷引用:河南省信阳市信阳高级中学2024届高三高考模拟(十)(3月月考)数学试题
名校
解题方法
4 . 已知直线AC与BD经过坐标原点O,且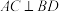 ,A、B、C、D均为圆
,A、B、C、D均为圆 上的点,则( )
上的点,则( )
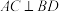 ,A、B、C、D均为圆
,A、B、C、D均为圆 上的点,则( )
上的点,则( )| A.圆心P到直线AC的距离的最小值为5 |
| B.弦AB,BC,CD,DA的中点满足四点共圆 |
C. 的最小值为 的最小值为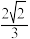 |
D.四边形ABCD的面积的取值范围是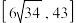 |
您最近半年使用:0次
23-24高三上·江西·阶段练习
名校
5 . 已知曲线 ,斜率为
,斜率为 的直线
的直线 经过点
经过点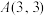 ,下列结论正确的是( )
,下列结论正确的是( )
 ,斜率为
,斜率为 的直线
的直线 经过点
经过点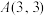 ,下列结论正确的是( )
,下列结论正确的是( )A. 的周长为 的周长为 |
B.若 与 与 恰有3个公共点,则 恰有3个公共点,则 的取值范围为 的取值范围为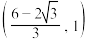 |
C.若 与 与 恰有2个公共点,则 恰有2个公共点,则 的取值范围为 的取值范围为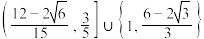 |
D.若 与 与 恰有1个公共点,则 恰有1个公共点,则 的取值范围为 的取值范围为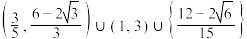 |
您最近半年使用:0次
解题方法
6 . 下列结论正确的是( )
A.若直线 : :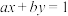 与圆 与圆 : :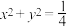 相交,则点 相交,则点 在圆 在圆 的外部 的外部 |
B.直线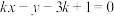 被圆 被圆 所截得的最长弦长为 所截得的最长弦长为 |
C.若圆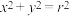 上有4个不同的点到直线 上有4个不同的点到直线 的距离为1,则有 的距离为1,则有 |
D.若过点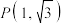 作圆 作圆 : :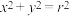 的切线只有一条,则切线方程为 的切线只有一条,则切线方程为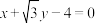 |
您最近半年使用:0次
名校
解题方法
7 . 已知圆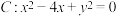 .
.
(1)若圆心 到直线
到直线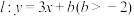 的距离为
的距离为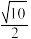 ,设
,设 是直线
是直线 上一动点,
上一动点, ,
, ,当
,当 最大时,求点
最大时,求点 坐标;
坐标;
(2)若过点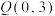 的直线
的直线 恰使圆
恰使圆 上有4个点到其距离为1,求直线
上有4个点到其距离为1,求直线 的斜率的取值范围.
的斜率的取值范围.
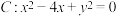 .
.(1)若圆心
 到直线
到直线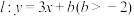 的距离为
的距离为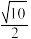 ,设
,设 是直线
是直线 上一动点,
上一动点, ,
, ,当
,当 最大时,求点
最大时,求点 坐标;
坐标;(2)若过点
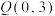 的直线
的直线 恰使圆
恰使圆 上有4个点到其距离为1,求直线
上有4个点到其距离为1,求直线 的斜率的取值范围.
的斜率的取值范围.
您最近半年使用:0次
2024-01-16更新
|
97次组卷
|
3卷引用:河北省沧州市泊头市第一中学2023-2024学年高二上学期1月月考数学试题
名校
解题方法
8 . 在平面直角坐标系 中,
中,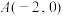 ,动点
,动点 满足
满足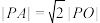 ,得到动点
,得到动点 的轨迹是曲线
的轨迹是曲线 .则下列说法正确的是( )
.则下列说法正确的是( )
 中,
中,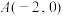 ,动点
,动点 满足
满足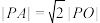 ,得到动点
,得到动点 的轨迹是曲线
的轨迹是曲线 .则下列说法正确的是( )
.则下列说法正确的是( )A.曲线 的方程为 的方程为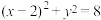 |
B.若直线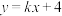 与曲线 与曲线 有公共点,则 有公共点,则 的取值范围是 的取值范围是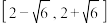 |
C.当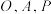 三点不共线时,若点 三点不共线时,若点 ,则射线 ,则射线 平分 平分 |
D.过曲线 外一点 外一点 作曲线 作曲线 的切线,切点分别为 的切线,切点分别为 ,则直线 ,则直线 过定点 过定点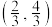 |
您最近半年使用:0次
2024-01-11更新
|
979次组卷
|
3卷引用:云南省昆明市第十四中学2023-2024学年高二下学期4月月考数学试卷
9 . 已知抛物线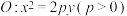 ,其顶点在坐标原点,直线
,其顶点在坐标原点,直线 与抛物线交于M,N两点,且
与抛物线交于M,N两点,且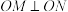 .
.
(1)求抛物线O的方程.
(2)已知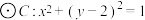 ,
, ,
, ,
, 是抛物线O上的三个点,且任意两点连线斜率都存在.其中
是抛物线O上的三个点,且任意两点连线斜率都存在.其中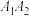 ,
,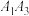 均与
均与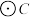 相切,请判断此时圆心
相切,请判断此时圆心 到直线
到直线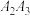 的距离是否为定值,如果是定值,请求出定值;若不是定值,请说明理由.
的距离是否为定值,如果是定值,请求出定值;若不是定值,请说明理由.
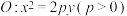 ,其顶点在坐标原点,直线
,其顶点在坐标原点,直线 与抛物线交于M,N两点,且
与抛物线交于M,N两点,且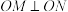 .
.(1)求抛物线O的方程.
(2)已知
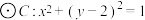 ,
, ,
, ,
, 是抛物线O上的三个点,且任意两点连线斜率都存在.其中
是抛物线O上的三个点,且任意两点连线斜率都存在.其中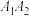 ,
,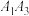 均与
均与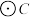 相切,请判断此时圆心
相切,请判断此时圆心 到直线
到直线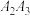 的距离是否为定值,如果是定值,请求出定值;若不是定值,请说明理由.
的距离是否为定值,如果是定值,请求出定值;若不是定值,请说明理由.
您最近半年使用:0次
名校
解题方法
10 . 对于直线 :
: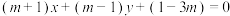 ,下列说法正确的有( )
,下列说法正确的有( )
 :
: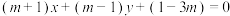 ,下列说法正确的有( )
,下列说法正确的有( )A.直线 恒过定点 恒过定点 |
B.无论m取何实数,直线 一定不过点 一定不过点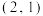 |
C.直线l被圆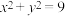 截得的最短弦长是2 截得的最短弦长是2 |
D.若直线 与圆 与圆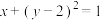 相切,则 相切,则 |
您最近半年使用:0次



