名校
1 . 已知椭圆 :
: 的右焦点为
的右焦点为 ,过点
,过点 作
作 轴的垂线交椭圆
轴的垂线交椭圆 于点
于点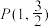 .过点
.过点 作椭圆
作椭圆 的切线,交
的切线,交 轴于点
轴于点 .
.
(1)求点 的坐标;
的坐标;
(2)过点 的直线(非
的直线(非 轴)交椭圆
轴)交椭圆 于
于 、
、 两点,过点
两点,过点 作
作 轴的垂线与直线
轴的垂线与直线 交于点
交于点 ,求证:线段
,求证:线段 的中点在定直线上.
的中点在定直线上.
 :
: 的右焦点为
的右焦点为 ,过点
,过点 作
作 轴的垂线交椭圆
轴的垂线交椭圆 于点
于点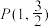 .过点
.过点 作椭圆
作椭圆 的切线,交
的切线,交 轴于点
轴于点 .
.(1)求点
 的坐标;
的坐标;(2)过点
 的直线(非
的直线(非 轴)交椭圆
轴)交椭圆 于
于 、
、 两点,过点
两点,过点 作
作 轴的垂线与直线
轴的垂线与直线 交于点
交于点 ,求证:线段
,求证:线段 的中点在定直线上.
的中点在定直线上.
您最近一年使用:0次
名校
解题方法
2 . 已知 ,直线
,直线 为平面内的一个动点,过点
为平面内的一个动点,过点 作
作 的垂线,垂足为
的垂线,垂足为 ,且
,且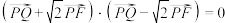 ,动点
,动点 的轨迹记为曲线
的轨迹记为曲线 .
.
(1)求 的方程;
的方程;
(2)若直线 交
交 于
于 两点,交圆
两点,交圆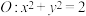 于
于 两点,且
两点,且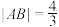 ,当
,当 的面积最大时,求
的面积最大时,求 的倾斜角.
的倾斜角.
 ,直线
,直线 为平面内的一个动点,过点
为平面内的一个动点,过点 作
作 的垂线,垂足为
的垂线,垂足为 ,且
,且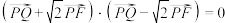 ,动点
,动点 的轨迹记为曲线
的轨迹记为曲线 .
.(1)求
 的方程;
的方程;(2)若直线
 交
交 于
于 两点,交圆
两点,交圆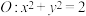 于
于 两点,且
两点,且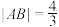 ,当
,当 的面积最大时,求
的面积最大时,求 的倾斜角.
的倾斜角.
您最近一年使用:0次
7日内更新
|
94次组卷
|
2卷引用:河北省南宫市私立丰翼中学2023-2024学年高二下学期第三次月考(5月)数学试卷
名校
3 . 已知椭圆 的左、右焦点分别为
的左、右焦点分别为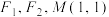 是
是 上一点,且点
上一点,且点 到点
到点 的距离之和为
的距离之和为 .
.
(1)求 的方程;
的方程;
(2)斜率为 的直线
的直线 与
与 交于
交于 两点,则
两点,则 的外心是否在一条定直线上?若在,求出该直线的方程;若不在,请说明理由.
的外心是否在一条定直线上?若在,求出该直线的方程;若不在,请说明理由.
 的左、右焦点分别为
的左、右焦点分别为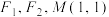 是
是 上一点,且点
上一点,且点 到点
到点 的距离之和为
的距离之和为 .
.(1)求
 的方程;
的方程;(2)斜率为
 的直线
的直线 与
与 交于
交于 两点,则
两点,则 的外心是否在一条定直线上?若在,求出该直线的方程;若不在,请说明理由.
的外心是否在一条定直线上?若在,求出该直线的方程;若不在,请说明理由.
您最近一年使用:0次
名校
解题方法
4 . 已知椭圆 的离心率为
的离心率为 ,左右焦点分别为
,左右焦点分别为 ,
, 是椭圆上一点,
是椭圆上一点,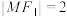 ,
,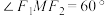 .
.
(1)求椭圆的方程;
(2)过点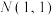 的直线与椭圆交于
的直线与椭圆交于 两点,
两点, 为线段
为线段 中点.
中点.
(i)求证: 点轨迹方程为
点轨迹方程为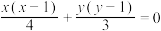 ;
;
(ii) 为坐标原点,射线
为坐标原点,射线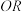 与椭圆交于点
与椭圆交于点 ,点
,点 为直线
为直线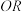 上一动点,且
上一动点,且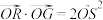 ,求证:点
,求证:点 在定直线上.
在定直线上.
 的离心率为
的离心率为 ,左右焦点分别为
,左右焦点分别为 ,
, 是椭圆上一点,
是椭圆上一点,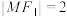 ,
,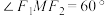 .
.(1)求椭圆的方程;
(2)过点
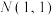 的直线与椭圆交于
的直线与椭圆交于 两点,
两点, 为线段
为线段 中点.
中点.(i)求证:
 点轨迹方程为
点轨迹方程为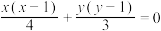 ;
;(ii)
 为坐标原点,射线
为坐标原点,射线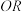 与椭圆交于点
与椭圆交于点 ,点
,点 为直线
为直线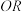 上一动点,且
上一动点,且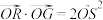 ,求证:点
,求证:点 在定直线上.
在定直线上.
您最近一年使用:0次
5 . 已知椭圆 的两个顶点分别为
的两个顶点分别为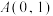 、
、 ,焦点在
,焦点在 轴上,离心率为
轴上,离心率为 ,直线
,直线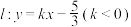 与椭圆
与椭圆 交于
交于 、
、 两点.
两点.
(1)求椭圆 的方程;
的方程;
(2)当 变化时,是否存在过点
变化时,是否存在过点 的定直线
的定直线 ,使直线
,使直线 平分
平分 ?若存在,求出该定直线的方程;若不存在,请说明理由.
?若存在,求出该定直线的方程;若不存在,请说明理由.
 的两个顶点分别为
的两个顶点分别为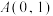 、
、 ,焦点在
,焦点在 轴上,离心率为
轴上,离心率为 ,直线
,直线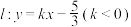 与椭圆
与椭圆 交于
交于 、
、 两点.
两点.(1)求椭圆
 的方程;
的方程;(2)当
 变化时,是否存在过点
变化时,是否存在过点 的定直线
的定直线 ,使直线
,使直线 平分
平分 ?若存在,求出该定直线的方程;若不存在,请说明理由.
?若存在,求出该定直线的方程;若不存在,请说明理由.
您最近一年使用:0次
6 . 已知圆 和点
和点 ,点
,点 是圆上任意一点,线段
是圆上任意一点,线段 的垂直平分线与线段
的垂直平分线与线段 相交于点
相交于点 ,记点
,记点 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线 的方程;
的方程;
(2)点 在直线
在直线 上运动,过点
上运动,过点 的动直线
的动直线 与曲线
与曲线 相交于点
相交于点 .
.
(ⅰ)若线段 上一点
上一点 ,满足
,满足 ,求证:当
,求证:当 的坐标为
的坐标为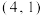 时,点
时,点 在定直线上;
在定直线上;
(ⅱ)过点 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,设直线
,设直线 的斜率分别为
的斜率分别为 ,当直线
,当直线 过点
过点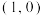 时,是否存在实数
时,是否存在实数 ,使得
,使得 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 和点
和点 ,点
,点 是圆上任意一点,线段
是圆上任意一点,线段 的垂直平分线与线段
的垂直平分线与线段 相交于点
相交于点 ,记点
,记点 的轨迹为曲线
的轨迹为曲线 .
.(1)求曲线
 的方程;
的方程;(2)点
 在直线
在直线 上运动,过点
上运动,过点 的动直线
的动直线 与曲线
与曲线 相交于点
相交于点 .
.(ⅰ)若线段
 上一点
上一点 ,满足
,满足 ,求证:当
,求证:当 的坐标为
的坐标为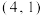 时,点
时,点 在定直线上;
在定直线上;(ⅱ)过点
 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,设直线
,设直线 的斜率分别为
的斜率分别为 ,当直线
,当直线 过点
过点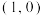 时,是否存在实数
时,是否存在实数 ,使得
,使得 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
2024-05-16更新
|
912次组卷
|
7卷引用:2024届山东省聊城市高三三模数学试题
2024届山东省聊城市高三三模数学试题(已下线)情境12 结论未知的证明命题(已下线)情境10 存在性探索命题2024届福建省厦门第一中学高考模拟(最后一卷)数学试题江苏省无锡市辅仁高级中学2024届高三下学期高考前适应性练习数学试题海南省2023-2024学年高二下学期期末数学考试试题福建省泉州市永春第一中学2024届高三最后一卷数学试卷
2024高三·全国·专题练习
解题方法
7 . 已知椭圆 的中心为坐标原点
的中心为坐标原点 ,对称轴为坐标轴,点
,对称轴为坐标轴,点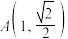 ,
,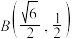 在椭圆
在椭圆 上.
上.
(1)求椭圆 的标准方程;
的标准方程;
(2)若椭圆 的左、右顶点分别为
的左、右顶点分别为 ,
, ,
, ,
, 为椭圆
为椭圆 上异于
上异于 ,
, 的两点,直线
的两点,直线 不过
不过 且不与坐标轴垂直,点
且不与坐标轴垂直,点 关于原点的对称点为
关于原点的对称点为 ,直线
,直线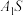 与直线
与直线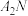 相交于点
相交于点 ,证明:直线
,证明:直线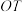 与直线
与直线 的交点在定直线上.
的交点在定直线上.
 的中心为坐标原点
的中心为坐标原点 ,对称轴为坐标轴,点
,对称轴为坐标轴,点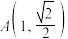 ,
,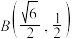 在椭圆
在椭圆 上.
上.(1)求椭圆
 的标准方程;
的标准方程;(2)若椭圆
 的左、右顶点分别为
的左、右顶点分别为 ,
, ,
, ,
, 为椭圆
为椭圆 上异于
上异于 ,
, 的两点,直线
的两点,直线 不过
不过 且不与坐标轴垂直,点
且不与坐标轴垂直,点 关于原点的对称点为
关于原点的对称点为 ,直线
,直线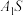 与直线
与直线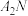 相交于点
相交于点 ,证明:直线
,证明:直线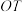 与直线
与直线 的交点在定直线上.
的交点在定直线上.
您最近一年使用:0次
2024高三下·全国·专题练习
8 . 已知椭圆 :
: (
( )过点
)过点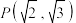 ,且离心率为
,且离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)记椭圆 的上下顶点分别为
的上下顶点分别为 ,过点
,过点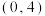 斜率为
斜率为 的直线与椭圆
的直线与椭圆 交于
交于 两点,证明:直线
两点,证明:直线 与
与 的交点
的交点 在定直线上,并求出该定直线的方程.
在定直线上,并求出该定直线的方程.
 :
: (
( )过点
)过点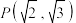 ,且离心率为
,且离心率为 .
.(1)求椭圆
 的方程;
的方程;(2)记椭圆
 的上下顶点分别为
的上下顶点分别为 ,过点
,过点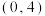 斜率为
斜率为 的直线与椭圆
的直线与椭圆 交于
交于 两点,证明:直线
两点,证明:直线 与
与 的交点
的交点 在定直线上,并求出该定直线的方程.
在定直线上,并求出该定直线的方程.
您最近一年使用:0次
解题方法
9 . 已知椭圆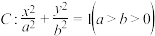 的离心率为
的离心率为 ,点
,点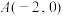 在
在 上.
上.
(1)求 的方程;
的方程;
(2)过点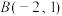 的直线交
的直线交 于P,Q两点,过点
于P,Q两点,过点 作垂直于
作垂直于 轴的直线与直线AQ相交于点
轴的直线与直线AQ相交于点 ,证明:线段PM的中点在定直线上.
,证明:线段PM的中点在定直线上.
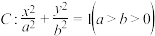 的离心率为
的离心率为 ,点
,点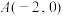 在
在 上.
上.(1)求
 的方程;
的方程;(2)过点
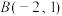 的直线交
的直线交 于P,Q两点,过点
于P,Q两点,过点 作垂直于
作垂直于 轴的直线与直线AQ相交于点
轴的直线与直线AQ相交于点 ,证明:线段PM的中点在定直线上.
,证明:线段PM的中点在定直线上.
您最近一年使用:0次
名校
解题方法
10 . 如图所示,在圆锥内放入两个球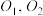 ,它们都与圆锥的侧面相切(即与圆锥的每条母线相切),且这两个球都与平面α相切,切点分别为
,它们都与圆锥的侧面相切(即与圆锥的每条母线相切),且这两个球都与平面α相切,切点分别为  ,数学家丹德林利用这个模型证明了平面α与圆锥侧面的交线为椭圆,记为Γ,
,数学家丹德林利用这个模型证明了平面α与圆锥侧面的交线为椭圆,记为Γ, 为椭圆Γ的两个焦点.设直线
为椭圆Γ的两个焦点.设直线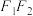 分别与该圆锥的母线交于A,B两点,过点A的母线分别与球
分别与该圆锥的母线交于A,B两点,过点A的母线分别与球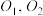 相切于 C,D 两点,已知
相切于 C,D 两点,已知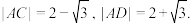 以直线
以直线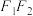 为x轴,在平面α内,以线段
为x轴,在平面α内,以线段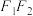 的中垂线为y轴,建立平面直角坐标系.
的中垂线为y轴,建立平面直角坐标系.
(2)点 T在直线 上,过点T作椭圆Γ的两条切线,切点分别为M,N,A,B分别是椭圆Γ的左、右顶点,连接
上,过点T作椭圆Γ的两条切线,切点分别为M,N,A,B分别是椭圆Γ的左、右顶点,连接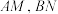 ,设直线
,设直线 与
与 交于点P.证明:点 P 在直线
交于点P.证明:点 P 在直线 上.
上.
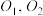 ,它们都与圆锥的侧面相切(即与圆锥的每条母线相切),且这两个球都与平面α相切,切点分别为
,它们都与圆锥的侧面相切(即与圆锥的每条母线相切),且这两个球都与平面α相切,切点分别为  ,数学家丹德林利用这个模型证明了平面α与圆锥侧面的交线为椭圆,记为Γ,
,数学家丹德林利用这个模型证明了平面α与圆锥侧面的交线为椭圆,记为Γ, 为椭圆Γ的两个焦点.设直线
为椭圆Γ的两个焦点.设直线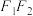 分别与该圆锥的母线交于A,B两点,过点A的母线分别与球
分别与该圆锥的母线交于A,B两点,过点A的母线分别与球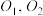 相切于 C,D 两点,已知
相切于 C,D 两点,已知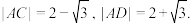 以直线
以直线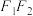 为x轴,在平面α内,以线段
为x轴,在平面α内,以线段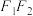 的中垂线为y轴,建立平面直角坐标系.
的中垂线为y轴,建立平面直角坐标系.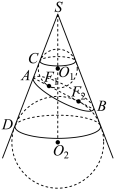
(2)点 T在直线
 上,过点T作椭圆Γ的两条切线,切点分别为M,N,A,B分别是椭圆Γ的左、右顶点,连接
上,过点T作椭圆Γ的两条切线,切点分别为M,N,A,B分别是椭圆Γ的左、右顶点,连接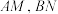 ,设直线
,设直线 与
与 交于点P.证明:点 P 在直线
交于点P.证明:点 P 在直线 上.
上.
您最近一年使用:0次
2024-04-18更新
|
584次组卷
|
3卷引用:2024届辽宁省抚顺市六校协作体高三下学期第三次模拟数学试卷



