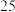解题方法
1 . 体育课的排球发球项目考试的规则是:每位学生最多可发球3次,一旦发球成功,则停止发球,否则一直发球到3次为止.设学生一次发球成功的概率为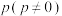 ,发球次数为
,发球次数为 ,若
,若 的均值
的均值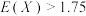 ,则
,则 的值可以为
的值可以为______ .(填一个符合题意的值即可)
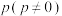 ,发球次数为
,发球次数为 ,若
,若 的均值
的均值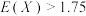 ,则
,则 的值可以为
的值可以为
您最近一年使用:0次
名校
2 . 当前,新一轮科技革命和产业变革蓬勃兴起,以区块链为代表的新一代信息技术迅猛发展,现收集某地近5年区块链企业总数量相关数据,如下表
(1)根据表中数据判断, 与
与 (其中
(其中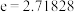 …为自然对数的底数),哪一个回归方程类型适宜预测未来几年我国区块链企业总数量?(给出结果即可,不必说明理由),并根据你的判断结果求y关于x的回归方程;
…为自然对数的底数),哪一个回归方程类型适宜预测未来几年我国区块链企业总数量?(给出结果即可,不必说明理由),并根据你的判断结果求y关于x的回归方程;
(2)为了促进公司间的合作与发展,区块链联合总部决定进行一次信息化技术比赛,邀请甲、乙、丙三家区块链公司参赛.比赛规则如下:①每场比赛有两个公司参加,并决出胜负;②每场比赛获胜的公司与未参加此场比赛的公司进行下一场的比赛;③在比赛中,若有一个公司首先获胜两场,则本次比赛结束,该公司获得此次信息化比赛的“优胜公司”.已知在每场比赛中,甲胜乙的概率为 ,甲胜丙的概率为
,甲胜丙的概率为 ,乙胜丙的概率为
,乙胜丙的概率为 ,若首场由甲乙比赛,求甲公司获得“优胜公司”的概率.
,若首场由甲乙比赛,求甲公司获得“优胜公司”的概率.
参考数据: ,
, ,
, ,
,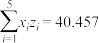 (其中
(其中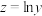 ).
).
附:样本 的最小二乘法估计公式为
的最小二乘法估计公式为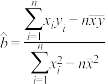 ,
,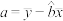 .
.
| 年份 | 2017 | 2018 | 2019 | 2020 | 2021 |
| 编号x | 1 | 2 | 3 | 4 | 5 |
| 企业总数量y(单位:千个) | 2.156 | 3.727 | 8.305 | 24.279 | 36.224 |
 与
与 (其中
(其中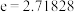 …为自然对数的底数),哪一个回归方程类型适宜预测未来几年我国区块链企业总数量?(给出结果即可,不必说明理由),并根据你的判断结果求y关于x的回归方程;
…为自然对数的底数),哪一个回归方程类型适宜预测未来几年我国区块链企业总数量?(给出结果即可,不必说明理由),并根据你的判断结果求y关于x的回归方程;(2)为了促进公司间的合作与发展,区块链联合总部决定进行一次信息化技术比赛,邀请甲、乙、丙三家区块链公司参赛.比赛规则如下:①每场比赛有两个公司参加,并决出胜负;②每场比赛获胜的公司与未参加此场比赛的公司进行下一场的比赛;③在比赛中,若有一个公司首先获胜两场,则本次比赛结束,该公司获得此次信息化比赛的“优胜公司”.已知在每场比赛中,甲胜乙的概率为
 ,甲胜丙的概率为
,甲胜丙的概率为 ,乙胜丙的概率为
,乙胜丙的概率为 ,若首场由甲乙比赛,求甲公司获得“优胜公司”的概率.
,若首场由甲乙比赛,求甲公司获得“优胜公司”的概率.参考数据:
 ,
, ,
, ,
,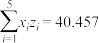 (其中
(其中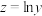 ).
).附:样本
 的最小二乘法估计公式为
的最小二乘法估计公式为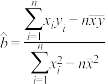 ,
,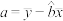 .
.
您最近一年使用:0次
2022-06-14更新
|
991次组卷
|
5卷引用:2023版 湘教版(2019) 选修第二册 过关斩将 第4章 本章复习提升
3 . 某公司为了解用户对其产品的满意度,从A、B两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:
(Ⅰ)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度的平均值及分散程度(不要求算出具体值,给出结论即可):
记事件C:“A地区用户的满意度等级高于B地区用户的满意度等级”,假设两地区用户的评价结果相互独立,根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率.
| A地区: | 62 | 73 | 81 | 92 | 95 | 85 | 74 | 64 | 53 | 76 |
| 78 | 86 | 95 | 66 | 97 | 78 | 88 | 82 | 76 | 89 | |
| B地区: | 73 | 83 | 62 | 51 | 91 | 46 | 53 | 73 | 64 | 82 |
| 93 | 48 | 95 | 81 | 74 | 56 | 54 | 76 | 65 | 79 |
(Ⅰ)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度的平均值及分散程度(不要求算出具体值,给出结论即可):
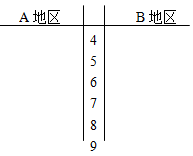
| 满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
| 满意度等级 | 不满意 | 满意 | 非常满意 |
记事件C:“A地区用户的满意度等级高于B地区用户的满意度等级”,假设两地区用户的评价结果相互独立,根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率.
您最近一年使用:0次
2016-12-03更新
|
11635次组卷
|
27卷引用:2015年全国普通高等学校招生统一考试理科数学(新课标Ⅱ)
2015年全国普通高等学校招生统一考试理科数学(新课标Ⅱ)2015-2016学年湖北省黄冈市蕲春县高二下期中理科数学试卷2018年春高考数学(理)二轮专题复习训练:专题六 计数原理、概率与统计、复数、算法四川省棠湖中学2018届高三3月月考数学(理)试题(已下线)《考前20天终极攻略》5月31日 统计【理科】(已下线)《高频考点解密》—解密24 统计人教A版(2019) 必修第二册 逆袭之路 第十章 10.2 事件的相互独立性沪教版(上海) 高三年级 新高考辅导与训练 第二部分 走近高考 第六章 概率高考题选(已下线)综合测试卷(基础版)突破满分数学之2019-2020学年高二数学(理)课时训练(人教A版选修2-3)(已下线)专题32 概率和统计【理】-十年(2011-2020)高考真题数学分项(六)(已下线)专题11.7 二项分布、正态分布(练)-2021年新高考数学一轮复习讲练测(已下线)专题23 概率与统计相结合问题(讲)-2021年高三数学二轮复习讲练测(新高考版)(已下线)专题27 概率与统计相结合问题(讲)-2021年高三数学二轮复习讲练测(文理通用)(已下线)专题14 概率统计-十年(2012-2021)高考数学真题分项汇编(全国通用)人教B版(2019) 选修第二册 过关检测 第四章 专题1 条件概率与独立事件的概率及其应用(已下线)专题11.7 二项分布、正态分布 2022年高考数学一轮复习讲练测(新教材新高考)(练)辽宁省名校联盟2021-2022学年高一3月联合考试数学试题沪教版(2020) 一轮复习 堂堂清 第九单元 综合练习湘教版(2019)必修第二册课本习题第5章复习题北师大版(2019)必修第一册课本习题第七章复习题(已下线)复习题七(已下线)专题25 概率统计解答题(理科)-3湖南省常德市2018-2019学年高二下学期期中数学(理)试题(已下线)专题10.6 二项分布及其应用(练)-浙江版《2020年高考一轮复习讲练测》山东省东营市广饶县第一中学2021-2022学年高一下学期开学考试数学试题山东省东营市广饶县第一中学2021-2022学年高一上学期第三次检测数学试题(已下线)复习题五3
4 . 全美数学竞赛(American Mathematics Competition, 简称AMC)共有25道选择题,每题6分,共150分.每道题有A,B,C,D,E共5个选项,只有一个正确选项.评分规则为:填写正确答案得6分,不填得2分,填错答案得0分.某考生考试快结束时,还余下2道题没有完成.若该考生随机选中5个选项中的某一个和不填这6种情况是等可能的.
(1)求他这2题恰好得到2分的概率;
(2)如果这2道题中,每道题均可随机猜一个答案填写或者不填,请从小到大列举出所有可能的得分.
(1)求他这2题恰好得到2分的概率;
(2)如果这2道题中,每道题均可随机猜一个答案填写或者不填,请从小到大列举出所有可能的得分.
您最近一年使用:0次
2020-11-20更新
|
586次组卷
|
4卷引用:专题11.4 随机事件的概率与古典概型(精练)-2021年新高考数学一轮复习学与练
(已下线)专题11.4 随机事件的概率与古典概型(精练)-2021年新高考数学一轮复习学与练(已下线)4.1.2、4.1.3 乘法公式与全概率公式、独立性与条件概率的关系-2020-2021学年高二数学课时同步练(人教B版2019选择性必修第二册)人教B版(2019) 选修第二册 过关检测 第四章 专题1 条件概率与独立事件的概率及其应用云南师范大学附属中学呈贡校区2020—2021学年高二上学期第一学段模块考试(期中考试)试题
2011·安徽·高考真题
5 . 本小题满分13分)
工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只派一次,工作时间不超过10分钟,如果有一个人10分钟内不能完成任务则撤出,再派下一个人.现在一共只有甲、乙、丙三个人可派,他们各自能完成任务的概率分别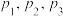
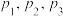 ,假设
,假设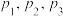 互不相等,且假定各人能否完成任务的事件相互独立.
互不相等,且假定各人能否完成任务的事件相互独立.
(1)如果按甲在先,乙次之,丙最后的顺序派人,求任务能被完成的概率.若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(2)若按某指定顺序派人,这三个人各自能完成任务的概率依次为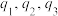 ,其中
,其中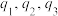 是
是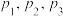 的一个排列,求所需派出人员数目
的一个排列,求所需派出人员数目 的分布列和均值(数字期望)
的分布列和均值(数字期望) ;
;
(3)假定 ,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小.
,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小.
工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只派一次,工作时间不超过10分钟,如果有一个人10分钟内不能完成任务则撤出,再派下一个人.现在一共只有甲、乙、丙三个人可派,他们各自能完成任务的概率分别
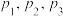
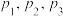 ,假设
,假设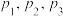 互不相等,且假定各人能否完成任务的事件相互独立.
互不相等,且假定各人能否完成任务的事件相互独立.(1)如果按甲在先,乙次之,丙最后的顺序派人,求任务能被完成的概率.若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(2)若按某指定顺序派人,这三个人各自能完成任务的概率依次为
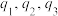 ,其中
,其中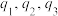 是
是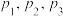 的一个排列,求所需派出人员数目
的一个排列,求所需派出人员数目 的分布列和均值(数字期望)
的分布列和均值(数字期望) ;
;(3)假定
 ,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小.
,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小.
您最近一年使用:0次
2019-01-30更新
|
2982次组卷
|
15卷引用:2011-2012学年黑龙江牡丹江一中高二下学期期末考试理科数学试卷
(已下线)2011-2012学年黑龙江牡丹江一中高二下学期期末考试理科数学试卷2017届河北定州中学高三上学期周练7.8数学试卷2019届湖南省长沙市湖南师范大学附中高三下学期考前演练(六)数学(理)试题江西省南昌市四校联盟2019-2020学年高三第二次联考数学(理)试题2020届黑龙江省牡丹江市第一高级中学高三4月线上线下教学检测数学(理)试题(已下线)考点35 离散型随机变量及其分布列、期望和方差-2021年新高考数学一轮复习考点扫描人教A版(2019) 选修第三册 一蹴而就 第七章 单元测试北京名校2023届高三一轮总复习 第9章 统计与概率 9.9 条件概率与事件的独立性2011年普通高中招生考试安徽省市高考理科数学(已下线)2010-2011学年福建省师大附中高二下学期期末模块测试数学(理2015-2016学年湖北孝感高中高二5月调研二理科数学试卷(已下线)2019届广东省深圳中学高三5月适应性考试数学(理)试题广东省实验中学2019-2020学年高三下学期线上考试数学(理)试题安徽省淮南市寿县第一中学2018-2019学年高二下学期期末数学(理)试题江西省景德镇一中2020-2021学年高二下学期期末数学(2班)试题
名校
6 . 某工厂生产一种汽车的元件,该元件是经过A,B,C三道工序加工而成的,A,B,C三道工序加工的元件合格率分别为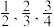 ,已知每道工序的加工都相互独立,三道工序加工都合格的元件为一等品;恰有两道工序加工合格的元件为二等品;其他的为废品,不进入市场.
,已知每道工序的加工都相互独立,三道工序加工都合格的元件为一等品;恰有两道工序加工合格的元件为二等品;其他的为废品,不进入市场.
(1)生产一个元件,求该元件为二等品的概率;
(2)从该工厂生产的这种元件中任意取出3个元件进行检测,求至少有2个元件是一等品的概率.
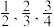 ,已知每道工序的加工都相互独立,三道工序加工都合格的元件为一等品;恰有两道工序加工合格的元件为二等品;其他的为废品,不进入市场.
,已知每道工序的加工都相互独立,三道工序加工都合格的元件为一等品;恰有两道工序加工合格的元件为二等品;其他的为废品,不进入市场.(1)生产一个元件,求该元件为二等品的概率;
(2)从该工厂生产的这种元件中任意取出3个元件进行检测,求至少有2个元件是一等品的概率.
您最近一年使用:0次
2021-09-07更新
|
725次组卷
|
10卷引用:2019年北京市西城区第二学期期末高二数学试卷
2019年北京市西城区第二学期期末高二数学试卷人教B版(2019) 必修第二册 过关斩将 第五章 5.3 概率 5.3.5 综合拔高练湖南省长沙市长郡中学2021-2022学年高二上学期入学考试数学试题北京师大附中2020-2021学年高二上学期期末试题北京市第十三中学2021-2022学年高二下学期期中数学试题山东省菏泽市定陶区明德学校(山大附中实验学校)2022-2023学年高一(创新部)下学期6月月考数学试题安徽省蚌埠市五河第一中学2021-2022学年高二上学期第一次月考数学试题广东省佛山市南海区西樵高级中学2021-2022学年高二上学期期中数学试题云南省大理州实验中学2021-2022学年高二上学期期中数学试题浙江省武义第一中学2023-2024学年高二上学期11月检测1数学试题
名校
7 . 一支担负勘探任务的队伍有若干个勘探小组和两类勘探人员,甲类人员应用某种新型勘探技术的精准率为0.6,乙类人员应用这种勘探技术的精准率为 .每个勘探小组配备1名甲类人员与2名乙类人员,假设在执行任务中每位人员均有一次应用这种技术的机会且互不影响,记在执行任务中每个勘探小组能精准应用这种新型技术的人员数量为
.每个勘探小组配备1名甲类人员与2名乙类人员,假设在执行任务中每位人员均有一次应用这种技术的机会且互不影响,记在执行任务中每个勘探小组能精准应用这种新型技术的人员数量为 .
.
(1)证明:在 各个取值对应的概率中,概率
各个取值对应的概率中,概率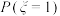 的值最大;
的值最大;
(2)在特殊的勘探任务中,每次只能派一个勘探小组出发,工作时间不超过半小时,如果半小时内无法完成任务,则重新派另一组出发.现在有三个勘探小组 可派出,若小组
可派出,若小组 能完成特殊任务的概率t;
能完成特殊任务的概率t;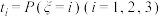 ,且各个小组能否完成任务相互独立.试分析以怎样的先后顺序派出勘探小组,可使在特殊勘探时所需派出的小组个数的均值达到最小.
,且各个小组能否完成任务相互独立.试分析以怎样的先后顺序派出勘探小组,可使在特殊勘探时所需派出的小组个数的均值达到最小.
 .每个勘探小组配备1名甲类人员与2名乙类人员,假设在执行任务中每位人员均有一次应用这种技术的机会且互不影响,记在执行任务中每个勘探小组能精准应用这种新型技术的人员数量为
.每个勘探小组配备1名甲类人员与2名乙类人员,假设在执行任务中每位人员均有一次应用这种技术的机会且互不影响,记在执行任务中每个勘探小组能精准应用这种新型技术的人员数量为 .
.(1)证明:在
 各个取值对应的概率中,概率
各个取值对应的概率中,概率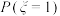 的值最大;
的值最大;(2)在特殊的勘探任务中,每次只能派一个勘探小组出发,工作时间不超过半小时,如果半小时内无法完成任务,则重新派另一组出发.现在有三个勘探小组
 可派出,若小组
可派出,若小组 能完成特殊任务的概率t;
能完成特殊任务的概率t;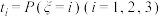 ,且各个小组能否完成任务相互独立.试分析以怎样的先后顺序派出勘探小组,可使在特殊勘探时所需派出的小组个数的均值达到最小.
,且各个小组能否完成任务相互独立.试分析以怎样的先后顺序派出勘探小组,可使在特殊勘探时所需派出的小组个数的均值达到最小.
您最近一年使用:0次
2021-03-22更新
|
2855次组卷
|
5卷引用:湖南省长沙市长郡中学2021届高三下学期月考(七)数学试题
湖南省长沙市长郡中学2021届高三下学期月考(七)数学试题湖北省武汉市2020-2021学年高二下学期第一次调研数学试题(已下线)第51讲 概率与统计综合问题-2022年新高考数学二轮专题突破精练(已下线)专题7.6第七章《随机变量及其分布列》综合测试卷(B卷提升篇)-2020-2021学年高二下学期数学选择性必修第三册同步单元AB卷(新教材人教A版,浙江专用)湖北省鄂州市2020-2021学年高二下学期期末数学试题
名校
解题方法
8 . 工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只派一次,工作时间不超过10分钟,如果有一个人10分钟内不能完成任务则撤出,再派下一个人.现在一共只有甲、乙、丙三个人可派,他们各自能完成任务的概率分别 ,
, ,
, ,假设
,假设 ,
, ,
, 互不相等,且假定各人能否完成任务的事件相互独立.
互不相等,且假定各人能否完成任务的事件相互独立.
(Ⅰ)如果按甲最先,乙次之,丙最后的顺序派人,求任务能被完成的概率.若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(Ⅱ)若按某指定顺序派人,这三个人各自能完成任务的概率依次为 ,
,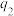 ,
,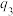 (
( ,
,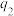 ,
,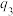 是
是 ,
, ,
, 的一个排列),求所需派出人员数目X的分布列和数学期望
的一个排列),求所需派出人员数目X的分布列和数学期望 (结果用
(结果用 ,
,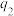 ,
,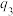 表示).
表示).
 ,
, ,
, ,假设
,假设 ,
, ,
, 互不相等,且假定各人能否完成任务的事件相互独立.
互不相等,且假定各人能否完成任务的事件相互独立.(Ⅰ)如果按甲最先,乙次之,丙最后的顺序派人,求任务能被完成的概率.若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(Ⅱ)若按某指定顺序派人,这三个人各自能完成任务的概率依次为
 ,
,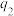 ,
,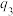 (
( ,
,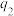 ,
,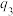 是
是 ,
, ,
, 的一个排列),求所需派出人员数目X的分布列和数学期望
的一个排列),求所需派出人员数目X的分布列和数学期望 (结果用
(结果用 ,
,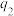 ,
,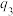 表示).
表示).
您最近一年使用:0次
名校
解题方法
9 . 有一个开房门的游戏,其玩法为:
盒中先放入两把钥匙 和两把钥匙
和两把钥匙 ,
, 能够打开房门,
能够打开房门, 不能打开房门.
不能打开房门.
每次从盒中随机取一把试开,试开后不放回钥匙.第一次打开房门后,关上门继续试开,第二次打开房门后停止抽取,称为进行了一轮游戏.
若每一轮取钥匙不超过三次,则该轮“成功”,否则为“失败”,如果某一轮“成功”,则游戏终止;若“失败”,则将所有钥匙重新放入盒中,并再放入一把钥匙 ,继续下一轮抽取,直至“成功”.
,继续下一轮抽取,直至“成功”.
(1)有 名爱好者独立参与这个游戏,记
名爱好者独立参与这个游戏,记 表示“成功”时抽取钥匙的轮次数,
表示“成功”时抽取钥匙的轮次数, 表示对应的人数,部分统计数据如下表:
表示对应的人数,部分统计数据如下表:
若将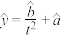 作为
作为 关于
关于 的经验回归方程,估计抽取
的经验回归方程,估计抽取 轮才“成功”的人数(人数精确到个位);
轮才“成功”的人数(人数精确到个位);
(2)由于时间关系,规定:进行游戏时,最多进行三轮,若均未“成功”也要终止游戏.求游戏要进行三轮的概率.
参考公式:最小二乘估计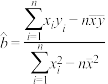 ,
,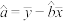 .
.
参考数据:取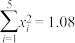 ,
,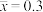 ,其中
,其中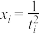 ,
,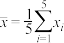 .
.
盒中先放入两把钥匙
 和两把钥匙
和两把钥匙 ,
, 能够打开房门,
能够打开房门, 不能打开房门.
不能打开房门.每次从盒中随机取一把试开,试开后不放回钥匙.第一次打开房门后,关上门继续试开,第二次打开房门后停止抽取,称为进行了一轮游戏.
若每一轮取钥匙不超过三次,则该轮“成功”,否则为“失败”,如果某一轮“成功”,则游戏终止;若“失败”,则将所有钥匙重新放入盒中,并再放入一把钥匙
 ,继续下一轮抽取,直至“成功”.
,继续下一轮抽取,直至“成功”.(1)有
 名爱好者独立参与这个游戏,记
名爱好者独立参与这个游戏,记 表示“成功”时抽取钥匙的轮次数,
表示“成功”时抽取钥匙的轮次数, 表示对应的人数,部分统计数据如下表:
表示对应的人数,部分统计数据如下表:
|
|
|
|
|
|
|
|
|
|
|
|
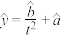 作为
作为 关于
关于 的经验回归方程,估计抽取
的经验回归方程,估计抽取 轮才“成功”的人数(人数精确到个位);
轮才“成功”的人数(人数精确到个位);(2)由于时间关系,规定:进行游戏时,最多进行三轮,若均未“成功”也要终止游戏.求游戏要进行三轮的概率.
参考公式:最小二乘估计
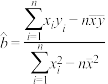 ,
,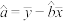 .
.参考数据:取
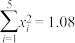 ,
,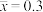 ,其中
,其中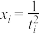 ,
,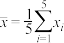 .
.
您最近一年使用:0次
2023-02-01更新
|
972次组卷
|
8卷引用:重庆市第八中学校2021-2022学年高二下学期期末数学试题
重庆市第八中学校2021-2022学年高二下学期期末数学试题(已下线)第八章 成对数据的统计分析 全章题型大总结 (精讲)-【精讲精练】2022-2023学年高二数学下学期同步精讲精练(人教A版2019选择性必修第三册)(已下线)9.1.1变量的相关性(2)(已下线)8.1.2 样本相关系数(分层作业)-【上好课】2022-2023学年高二数学同步备课系列(人教A版2019选修第三册)(已下线)第05讲 第八章 成对数据的统计分析 章末重点题型大总结-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)8.2 一元线性回归模型及其应用——课后作业(巩固版)(已下线)9.1.1 变量的相关性(练习)-2022-2023学年高二数学同步精品课堂(苏教版2019选择性必修第二册)(已下线)9.1.2 线性回归方程-【题型分类归纳】2022-2023学年高二数学同步讲与练(苏教版2019选择性必修第二册)
解题方法
10 . 在箱子中有大小相同,仅颜色不同的小球共6个,其中红色小球2个,白色小球4个.现从箱子中每次随机取出一个小球,若取出的是白球,放回,并继续从箱子中随机取出一个小球;若取出的是红色小球,不放回,并继续从箱子中随机取出一个小球.直到取出2个红色小球结束.
(1)若在第一次取出的小球是红球的条件下,求取球4次结束的概率;
(2)求取球结束时,取球次数不超过3次的概率.
(1)若在第一次取出的小球是红球的条件下,求取球4次结束的概率;
(2)求取球结束时,取球次数不超过3次的概率.
您最近一年使用:0次