1 . 如图,在四棱锥 中,
中,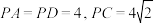 ,底面
,底面 是直角梯形,
是直角梯形,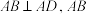

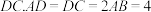 .
. 平面
平面 ;
;
(2)求证: ;
;
(3)求平面 与平面
与平面 夹角的余弦值.
夹角的余弦值.
 中,
中,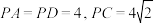 ,底面
,底面 是直角梯形,
是直角梯形,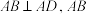

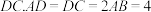 .
.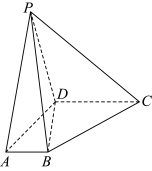
 平面
平面 ;
;(2)求证:
 ;
;(3)求平面
 与平面
与平面 夹角的余弦值.
夹角的余弦值.
您最近一年使用:0次
2 . 人脸识别是基于人的脸部特征进行身份识别的一种生物识别技术,主要应用距离测试样本之间的相似度.在平面直角坐标系 中,
中,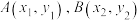 ,定义两种距离:欧几里得距离
,定义两种距离:欧几里得距离 ;曼哈顿距离
;曼哈顿距离 .
.
(1)求满足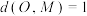 的点
的点 的轨迹所围成的图形面积;
的轨迹所围成的图形面积;
(2)在 中,求证:
中,求证: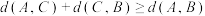 ;
;
(3)已知点 是直线
是直线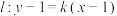 上的两动点,问是否存在直线
上的两动点,问是否存在直线 使得
使得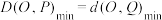 ?若存在,求出所有满足条件的直线
?若存在,求出所有满足条件的直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
 中,
中,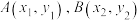 ,定义两种距离:欧几里得距离
,定义两种距离:欧几里得距离 ;曼哈顿距离
;曼哈顿距离 .
.(1)求满足
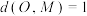 的点
的点 的轨迹所围成的图形面积;
的轨迹所围成的图形面积;(2)在
 中,求证:
中,求证: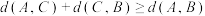 ;
;(3)已知点
 是直线
是直线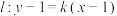 上的两动点,问是否存在直线
上的两动点,问是否存在直线 使得
使得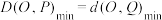 ?若存在,求出所有满足条件的直线
?若存在,求出所有满足条件的直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
您最近一年使用:0次
解题方法
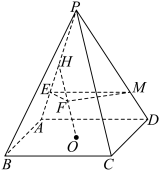
3 . 在正四棱锥 中,
中, 为底面中心,
为底面中心, ,
, ,
, 分别为
分别为 ,
, ,
,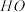 的中点,点
的中点,点 在棱
在棱 上,且
上,且 .
.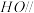 平面
平面 .
.
(2)证明:平面 平面
平面 .
.
 中,
中, 为底面中心,
为底面中心, ,
, ,
, 分别为
分别为 ,
, ,
,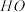 的中点,点
的中点,点 在棱
在棱 上,且
上,且 .
.
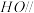 平面
平面 .
.(2)证明:平面
 平面
平面 .
.
您最近一年使用:0次
2024-11-02更新
|
668次组卷
|
2卷引用:贵州省遵义市多校2024-2025学年高二上学期10月联考数学试题
4 . 已知圆 的圆心
的圆心 在直线
在直线 上,并且经过点
上,并且经过点 ,与直线
,与直线 相切.
相切.
(1)求圆 的方程;
的方程;
(2)经过点 的直线
的直线 与圆
与圆 相交于A,B两点,若
相交于A,B两点,若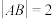 ,求直线
,求直线 的方程.
的方程.
 的圆心
的圆心 在直线
在直线 上,并且经过点
上,并且经过点 ,与直线
,与直线 相切.
相切.(1)求圆
 的方程;
的方程;(2)经过点
 的直线
的直线 与圆
与圆 相交于A,B两点,若
相交于A,B两点,若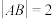 ,求直线
,求直线 的方程.
的方程.
您最近一年使用:0次
2024-10-30更新
|
888次组卷
|
2卷引用:贵州省贵阳市清华中学2024-2025学年高二上学期10月阶段考试数学试卷
5 . 已知动点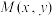 与点
与点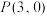 的距离是它与原点
的距离是它与原点 的距离的2倍.
的距离的2倍.
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)求 的最小值;
的最小值;
(3)经过原点 的两条互相垂直的直线分别与轨迹
的两条互相垂直的直线分别与轨迹 相交于
相交于 ,
, 两点和
两点和 ,
, 两点,求四边形ACBD的面积
两点,求四边形ACBD的面积 的最大值.
的最大值.
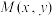 与点
与点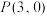 的距离是它与原点
的距离是它与原点 的距离的2倍.
的距离的2倍.(1)求动点
 的轨迹
的轨迹 的方程;
的方程;(2)求
 的最小值;
的最小值;(3)经过原点
 的两条互相垂直的直线分别与轨迹
的两条互相垂直的直线分别与轨迹 相交于
相交于 ,
, 两点和
两点和 ,
, 两点,求四边形ACBD的面积
两点,求四边形ACBD的面积 的最大值.
的最大值.
您最近一年使用:0次
名校
解题方法
6 . 已知直线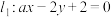 ,直线
,直线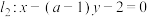 .
.
(1)若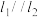 ,求
,求 ,
, 之间的距离;
之间的距离;
(2)若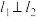 ,求
,求 ,
, 及
及 轴围成的三角形的面积.
轴围成的三角形的面积.
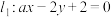 ,直线
,直线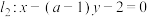 .
.(1)若
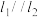 ,求
,求 ,
, 之间的距离;
之间的距离;(2)若
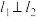 ,求
,求 ,
, 及
及 轴围成的三角形的面积.
轴围成的三角形的面积.
您最近一年使用:0次
2024-10-21更新
|
938次组卷
|
3卷引用:贵州省毕节市金沙县实验高级中学2024-2025学年高二上学期第一次月考数学试卷
7 . (1)设平面直角坐标系内三点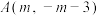 、
、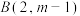 、
、 ,若直线
,若直线 的斜率是直线
的斜率是直线 的斜率的3倍,求实数
的斜率的3倍,求实数 的值;
的值;
(2)已知直线 经过原点,且经过两条直线
经过原点,且经过两条直线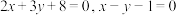 的交点,求直线
的交点,求直线 的方程.
的方程.
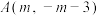 、
、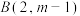 、
、 ,若直线
,若直线 的斜率是直线
的斜率是直线 的斜率的3倍,求实数
的斜率的3倍,求实数 的值;
的值;(2)已知直线
 经过原点,且经过两条直线
经过原点,且经过两条直线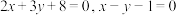 的交点,求直线
的交点,求直线 的方程.
的方程.
您最近一年使用:0次
解题方法
8 . (1)若直线 沿
沿 轴向右平移5个单位长度,再沿
轴向右平移5个单位长度,再沿 轴向上平移2个单位长度后,回到原来的位置,求
轴向上平移2个单位长度后,回到原来的位置,求 的斜率;
的斜率;
(2)一束光线从点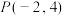 射出,与
射出,与 轴相交于点
轴相交于点 ,经
,经 轴反射,求入射光线和反射光线所在直线的方程.
轴反射,求入射光线和反射光线所在直线的方程.
 沿
沿 轴向右平移5个单位长度,再沿
轴向右平移5个单位长度,再沿 轴向上平移2个单位长度后,回到原来的位置,求
轴向上平移2个单位长度后,回到原来的位置,求 的斜率;
的斜率;(2)一束光线从点
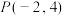 射出,与
射出,与 轴相交于点
轴相交于点 ,经
,经 轴反射,求入射光线和反射光线所在直线的方程.
轴反射,求入射光线和反射光线所在直线的方程.
您最近一年使用:0次
2024-10-12更新
|
235次组卷
|
2卷引用:贵州省毕节市金沙县实验高级中学2024-2025学年高二上学期第一次月考数学试卷
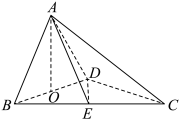
9 . 如图,四面体 中,
中,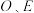 分别
分别 的中点,
的中点, ,
,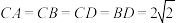 .
.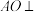 平面
平面 ;
;
(2)求点 到平面
到平面 的距离.
的距离.
 中,
中,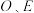 分别
分别 的中点,
的中点, ,
,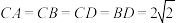 .
.
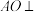 平面
平面 ;
;(2)求点
 到平面
到平面 的距离.
的距离.
您最近一年使用:0次
名校
解题方法
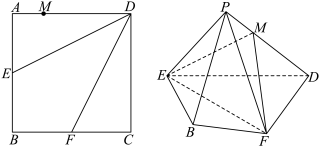
10 . 如图,在正方形 中,点
中,点 是
是 的中点,点
的中点,点 是
是 的中点,点
的中点,点 是
是 上一点,将
上一点,将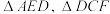 分别沿
分别沿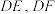 折起,使
折起,使 两点重合于
两点重合于 ,如图,连接
,如图,连接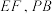 .
.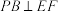 ;
;
(2)点 是
是 上一点,若
上一点,若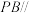 平面
平面 ,则
,则 为何值?并说明理由;
为何值?并说明理由;
(3)若点 满足(2),求二面角
满足(2),求二面角 的余弦值.
的余弦值.
 中,点
中,点 是
是 的中点,点
的中点,点 是
是 的中点,点
的中点,点 是
是 上一点,将
上一点,将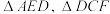 分别沿
分别沿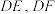 折起,使
折起,使 两点重合于
两点重合于 ,如图,连接
,如图,连接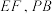 .
.
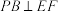 ;
;(2)点
 是
是 上一点,若
上一点,若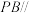 平面
平面 ,则
,则 为何值?并说明理由;
为何值?并说明理由;(3)若点
 满足(2),求二面角
满足(2),求二面角 的余弦值.
的余弦值.
您最近一年使用:0次



