1 . 设 是定义在R上的函数,其导函数为
是定义在R上的函数,其导函数为 .
.
(1)若函数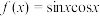 ,求
,求 的值;
的值;
(2)若 是奇函数,当
是奇函数,当 时,恒有
时,恒有 ,求不等式
,求不等式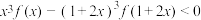 的解集;
的解集;
(3)若对于任意的实数 都有
都有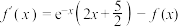 ,且
,且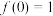 ,若关于
,若关于 的不等式
的不等式 的解集中恰有唯一的一个整数,求实数
的解集中恰有唯一的一个整数,求实数 的取值范围.
的取值范围.
 是定义在R上的函数,其导函数为
是定义在R上的函数,其导函数为 .
.(1)若函数
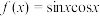 ,求
,求 的值;
的值;(2)若
 是奇函数,当
是奇函数,当 时,恒有
时,恒有 ,求不等式
,求不等式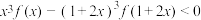 的解集;
的解集;(3)若对于任意的实数
 都有
都有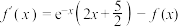 ,且
,且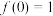 ,若关于
,若关于 的不等式
的不等式 的解集中恰有唯一的一个整数,求实数
的解集中恰有唯一的一个整数,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
2 . 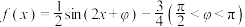 ,且
,且 .
.
(1)方程 在
在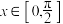 有且仅有一个解,求
有且仅有一个解,求 的取值范围.
的取值范围.
(2)设 ,对
,对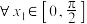 ,总
,总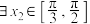 ,使
,使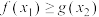 成立,求
成立,求 的范围.
的范围.
(3)若 与
与 的图象关于
的图象关于 对称,求不等式
对称,求不等式 的解集.
的解集.
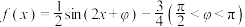 ,且
,且 .
.(1)方程
 在
在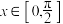 有且仅有一个解,求
有且仅有一个解,求 的取值范围.
的取值范围.(2)设
 ,对
,对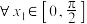 ,总
,总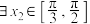 ,使
,使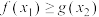 成立,求
成立,求 的范围.
的范围.(3)若
 与
与 的图象关于
的图象关于 对称,求不等式
对称,求不等式 的解集.
的解集.
您最近一年使用:0次
2023-05-21更新
|
1297次组卷
|
6卷引用:江西省吉安市双校联盟2022-2023学年高一下学期期中考试数学试题
江西省吉安市双校联盟2022-2023学年高一下学期期中考试数学试题(已下线)模块四 专题2 重组综合练(江西)(北师版高一期中)辽宁省沈阳市第十一中学2022-2023学年高一下学期4月月考数学试题(已下线)专题5.9 三角函数全章八类必考压轴题-举一反三系列(已下线)专题5.4 三角函数的图象与性质-举一反三系列(已下线)第七章 三角函数(压轴题专练)-单元速记·巧练(沪教版2020必修第二册)
名校
3 . 已知不等式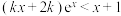 恰有2个非负整数解,则实数
恰有2个非负整数解,则实数 的取值范围( )
的取值范围( )
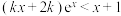 恰有2个非负整数解,则实数
恰有2个非负整数解,则实数 的取值范围( )
的取值范围( )A.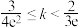 | B.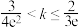 | C.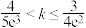 | D.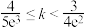 |
您最近一年使用:0次
2024-08-29更新
|
509次组卷
|
2卷引用:安徽省马鞍山中加双语学校2022-2023学年高二下学期数学期中考试试题
名校
解题方法
4 . 已知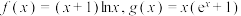 (其中
(其中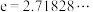 为自然对数的底数),则下列结论正确的是( )
为自然对数的底数),则下列结论正确的是( )
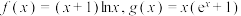 (其中
(其中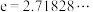 为自然对数的底数),则下列结论正确的是( )
为自然对数的底数),则下列结论正确的是( )A. 为函数 为函数 的导函数,则方程 的导函数,则方程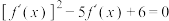 有3个不等的实数解 有3个不等的实数解 |
B.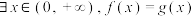 |
C.若对任意 ,不等式 ,不等式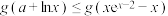 恒成立,则实数 恒成立,则实数 的最大值为-1 的最大值为-1 |
D.若 ,则 ,则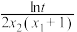 的最大值为 的最大值为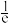 |
您最近一年使用:0次
2024-01-29更新
|
1892次组卷
|
3卷引用:四川省眉山市东坡区永寿高级中学2023-2024学年高二下学期4月期中联考数学试题
四川省眉山市东坡区永寿高级中学2023-2024学年高二下学期4月期中联考数学试题吉林省长春市五校2023-2024学年高三上学期联合模拟考试数学试题(已下线)2024年高考数学全真模拟卷08(新题型地区专用)
5 . 已知函数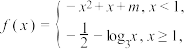
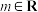 ,
, ,给出下列四个结论:
,给出下列四个结论:
①函数 在区间
在区间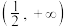 上单调递减;
上单调递减;
②函数 的最大值是
的最大值是 ;
;
③若关于 的方程
的方程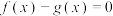 有且只有一个实数解,则
有且只有一个实数解,则 的最小值为
的最小值为 ;
;
④若对于任意实数a,b,不等式 都成立,则
都成立,则 的取值范围是
的取值范围是 .
.
其中所有正确结论的序号是_______ .
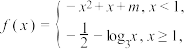
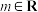 ,
, ,给出下列四个结论:
,给出下列四个结论:①函数
 在区间
在区间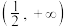 上单调递减;
上单调递减;②函数
 的最大值是
的最大值是 ;
;③若关于
 的方程
的方程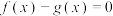 有且只有一个实数解,则
有且只有一个实数解,则 的最小值为
的最小值为 ;
;④若对于任意实数a,b,不等式
 都成立,则
都成立,则 的取值范围是
的取值范围是 .
.其中所有正确结论的序号是
您最近一年使用:0次
名校
6 . 若关于 的不等式
的不等式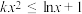 的解集中恰有2个整数,则
的解集中恰有2个整数,则 的取值范围是( )
的取值范围是( )
 的不等式
的不等式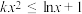 的解集中恰有2个整数,则
的解集中恰有2个整数,则 的取值范围是( )
的取值范围是( )A. | B.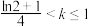 |
C.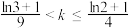 | D.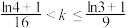 |
您最近一年使用:0次
2023-06-18更新
|
569次组卷
|
4卷引用:四川省成都市蓉城名校联盟2022-2023学年高二下学期期中联考数学文科试题
名校
解题方法
7 . 已知函数 的导函数为
的导函数为 ,且对任意的实数
,且对任意的实数 都有
都有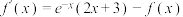 (
( 是自然对数的底数),且
是自然对数的底数),且 ,若关于
,若关于 的不等式
的不等式 的解集中恰有两个整数,则实数
的解集中恰有两个整数,则实数 的取值范围是( )
的取值范围是( )
 的导函数为
的导函数为 ,且对任意的实数
,且对任意的实数 都有
都有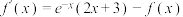 (
( 是自然对数的底数),且
是自然对数的底数),且 ,若关于
,若关于 的不等式
的不等式 的解集中恰有两个整数,则实数
的解集中恰有两个整数,则实数 的取值范围是( )
的取值范围是( )A.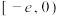 | B. | C.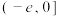 | D.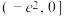 |
您最近一年使用:0次
2020-12-03更新
|
2028次组卷
|
21卷引用:四川省眉山市东坡区永寿高级中学2019-2020学年高二下学期期中考试数学(理)试题
四川省眉山市东坡区永寿高级中学2019-2020学年高二下学期期中考试数学(理)试题四川省眉山市东坡区永寿高级中学2019-2020学年高二下学期期中考试数学(文)试题甘肃省兰州市西北师范大学附属中学2020-2021学年高三数学第一学期期中试题安徽省合肥市第一中学2023-2024学年高二下学期期中联考数学试题【全国百强校】湖南省长沙市长郡中学2018届高考模拟卷(二)理科数学试题【全国校级联考】山东、湖北部分重点中学2018届高三高考冲刺模拟试卷(五) 文科数学试题四川省华蓥市第一中学2019届高三入学调研考试理科数学试题【全国校级联考】安徽省淮北部分校2019届高三上学期开学联考理科数学试题【省级联考】福建省2019届高中毕业班数学学科备考关键问题指导系列数学(文科)适应性练习(二)福建省福州市八县(市)一中2018-2019学年高二下学期期末联考数学(理)试题2020届安徽省合肥一中高三上学期11月阶段性考试数学(理)试题2020届重庆市名校联盟高三二诊数学(文)试题(已下线)重难点 06 函数与导数-2021年高考数学(理)【热点·重点·难点】专练(已下线)专题03 利用导数解不等式 第一篇 热点、难点突破篇(练) - 2021年高考二轮复习讲练测(浙江专用)广西柳州市2021届高三第一次模拟考试数学(理)试题江苏省南京市中华中学2021-2022学年高三上学期期初数学试题四川省广安代市中学校2021-2022学年高三上学期入学考试数学(理)试题(已下线)专题5.3 导数及其应用 章末检测3(难)-【满分计划】2021-2022学年高二数学阶段性复习测试卷(苏教版2019选择性必修第一册)(已下线)专题7.3 期末押题检测卷(考试范围:选择性必修第一册)3(难)-【满分计划】2021-2022学年高二数学阶段性复习测试卷(苏教版2019选择性必修第一册)湖南省长沙市雅礼中学2022-2023学年高二下学期3月第一次月考数学试题(已下线)大招26整数解问题
名校
解题方法
8 . 已知若 ,则称
,则称 为
为 的原函数,此时
的原函数,此时 所有的原函数为
所有的原函数为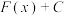 ,其中
,其中 为常数,如:
为常数,如: ,则
,则 (
( 为常数).现已知函数
为常数).现已知函数 的导函数为
的导函数为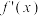 且对任意的实数
且对任意的实数 都有
都有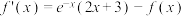 (
( 是自然对数的底数),且
是自然对数的底数),且 ,若关于
,若关于 的不等式
的不等式 的解集中恰有两个整数,则实数
的解集中恰有两个整数,则实数 的取值范围是
的取值范围是
 ,则称
,则称 为
为 的原函数,此时
的原函数,此时 所有的原函数为
所有的原函数为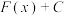 ,其中
,其中 为常数,如:
为常数,如: ,则
,则 (
( 为常数).现已知函数
为常数).现已知函数 的导函数为
的导函数为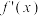 且对任意的实数
且对任意的实数 都有
都有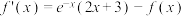 (
( 是自然对数的底数),且
是自然对数的底数),且 ,若关于
,若关于 的不等式
的不等式 的解集中恰有两个整数,则实数
的解集中恰有两个整数,则实数 的取值范围是
的取值范围是A. | B.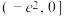 | C.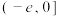 | D.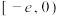 |
您最近一年使用:0次
9 . 已知函数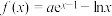 .
.
(1)若 是
是 的极值点,求
的极值点,求 的单调区间;
的单调区间;
(2)若关于 的方程
的方程 恰有一个解,求a的取值范围.
恰有一个解,求a的取值范围.
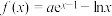 .
.(1)若
 是
是 的极值点,求
的极值点,求 的单调区间;
的单调区间;(2)若关于
 的方程
的方程 恰有一个解,求a的取值范围.
恰有一个解,求a的取值范围.
您最近一年使用:0次
2022-09-29更新
|
548次组卷
|
8卷引用:青海省西宁市湟中区2022-2023学年高三上学期期中考试数学(理)试题
名校
10 . 已知函数 在
在 处取得极值0.
处取得极值0.
(1)求实数 ,
, 的值;
的值;
(2)若关于 的方程
的方程 在区间
在区间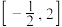 上恰有2个不同的实数解,求
上恰有2个不同的实数解,求 的取值范围;
的取值范围;
(3)设函数 ,若
,若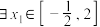 ,
,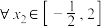 总有
总有 成立,求
成立,求 的取值范围.
的取值范围.
 在
在 处取得极值0.
处取得极值0.(1)求实数
 ,
, 的值;
的值;(2)若关于
 的方程
的方程 在区间
在区间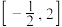 上恰有2个不同的实数解,求
上恰有2个不同的实数解,求 的取值范围;
的取值范围;(3)设函数
 ,若
,若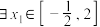 ,
, 总有
总有 成立,求
成立,求 的取值范围.
的取值范围.
您最近一年使用:0次
2022-11-10更新
|
611次组卷
|
3卷引用:天津市部分区2022-2023学年高三上学期期中数学试题



