名校
解题方法
1 . 下列说法正确的是( )
A.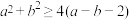 |
B.函数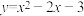 的零点为 的零点为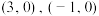 |
C.“ ”是“ ”是“ ”的充分不必要条件 ”的充分不必要条件 |
D.由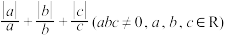 所确定的实数集合为 所确定的实数集合为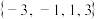 |
您最近一年使用:0次
2 . 动点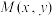 到直线
到直线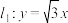 与直线
与直线 的距离之积等于
的距离之积等于 ,且
,且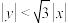 .记点M的轨迹方程为
.记点M的轨迹方程为 .
.
(1)求 的方程;
的方程;
(2)过 上的点P作圆
上的点P作圆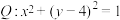 的切线PT,T为切点,求
的切线PT,T为切点,求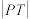 的最小值;
的最小值;
(3)已知点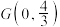 ,直线
,直线 交
交 于点A,B,
于点A,B, 上是否存在点C满足
上是否存在点C满足 ?若存在,求出点C的坐标;若不存在,说明理由.
?若存在,求出点C的坐标;若不存在,说明理由.
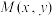 到直线
到直线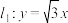 与直线
与直线 的距离之积等于
的距离之积等于 ,且
,且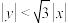 .记点M的轨迹方程为
.记点M的轨迹方程为 .
.(1)求
 的方程;
的方程;(2)过
 上的点P作圆
上的点P作圆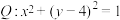 的切线PT,T为切点,求
的切线PT,T为切点,求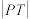 的最小值;
的最小值;(3)已知点
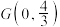 ,直线
,直线 交
交 于点A,B,
于点A,B, 上是否存在点C满足
上是否存在点C满足 ?若存在,求出点C的坐标;若不存在,说明理由.
?若存在,求出点C的坐标;若不存在,说明理由.
您最近一年使用:0次
2024-09-06更新
|
799次组卷
|
4卷引用:广西柳州高级中学2024-2025学年高三上学期9月自主综合考试数学试题
名校
解题方法
3 . 已知抛物线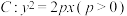 的准线l与圆
的准线l与圆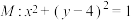 相切,P为C上的动点,N是圆M上的动点,过P作l的垂线,垂足为Q,C的焦点为F,则下列结论正确的是( )
相切,P为C上的动点,N是圆M上的动点,过P作l的垂线,垂足为Q,C的焦点为F,则下列结论正确的是( )
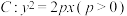 的准线l与圆
的准线l与圆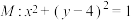 相切,P为C上的动点,N是圆M上的动点,过P作l的垂线,垂足为Q,C的焦点为F,则下列结论正确的是( )
相切,P为C上的动点,N是圆M上的动点,过P作l的垂线,垂足为Q,C的焦点为F,则下列结论正确的是( )A.点F的坐标为 |
B. 的最小值为 的最小值为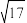 |
C.存在两个P点,使得 |
D.若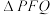 为正三角形,则圆M与直线PQ相交 为正三角形,则圆M与直线PQ相交 |
您最近一年使用:0次
2024-08-13更新
|
657次组卷
|
3卷引用:广西柳州高级中学2024-2025学年高三上学期阶段性测试(二)数学试题
4 . M是一个动点,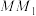 与直线
与直线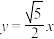 垂直,垂足
垂直,垂足 位于第一象限,
位于第一象限,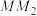 与直线
与直线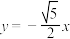 垂直,垂足
垂直,垂足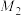 位于第四象限,且
位于第四象限,且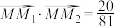 .
.
(1)求动点M的轨迹方程E;
(2)设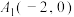 ,
, ,过点
,过点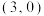 的直线l与曲线E交于A,B两点(点A在x轴上方),P为直线
的直线l与曲线E交于A,B两点(点A在x轴上方),P为直线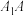 ,
,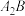 的交点,当点P的纵坐标为
的交点,当点P的纵坐标为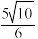 时,求直线l的方程.
时,求直线l的方程.
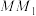 与直线
与直线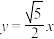 垂直,垂足
垂直,垂足 位于第一象限,
位于第一象限,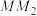 与直线
与直线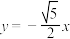 垂直,垂足
垂直,垂足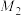 位于第四象限,且
位于第四象限,且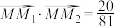 .
.(1)求动点M的轨迹方程E;
(2)设
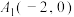 ,
, ,过点
,过点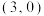 的直线l与曲线E交于A,B两点(点A在x轴上方),P为直线
的直线l与曲线E交于A,B两点(点A在x轴上方),P为直线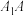 ,
,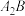 的交点,当点P的纵坐标为
的交点,当点P的纵坐标为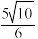 时,求直线l的方程.
时,求直线l的方程.
您最近一年使用:0次
5 . 下列说法正确的是( )
A.圆心角为 且半径为 且半径为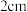 的扇形面积为 的扇形面积为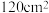 |
B.命题“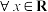 , ,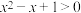 ”的否定是“ ”的否定是“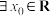 , , ” ” |
C. |
D.函数 的最小正周期为 的最小正周期为 |
您最近一年使用:0次
名校
解题方法
6 . 已知抛物线 过点
过点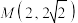 ,焦点为F,则( )
,焦点为F,则( )
 过点
过点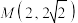 ,焦点为F,则( )
,焦点为F,则( )| A.点M到焦点的距离为3 |
| B.直线MF与x轴垂直 |
| C.直线MF与C交于点N,以弦MN为直径的圆与C的准线相切 |
D.过点M与C相切的直线方程为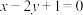 |
您最近一年使用:0次
2022-04-28更新
|
890次组卷
|
3卷引用:广西柳州高级中学2022-2023学年高二下学期2月月考数学试卷
广西柳州高级中学2022-2023学年高二下学期2月月考数学试卷辽宁省葫芦岛市2022届高三第一次模拟考试数学试题(已下线)考点22 抛物线-1-(核心考点讲与练)-2023年高考数学一轮复习核心考点讲与练(新高考专用)
名校
解题方法
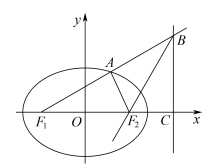
7 . 如图,椭圆的焦点在x轴上,长轴长为 ,离心率为
,离心率为 ,左、右焦点分别为
,左、右焦点分别为 ,
, ,若椭圆上第一象限的一个点A满足:直线
,若椭圆上第一象限的一个点A满足:直线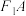 与直线
与直线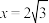 的交点为B,直线
的交点为B,直线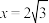 与x轴的交点为C,且射线
与x轴的交点为C,且射线 为∠ABC的角平分线,则
为∠ABC的角平分线,则 的面积为( )
的面积为( )
 ,离心率为
,离心率为 ,左、右焦点分别为
,左、右焦点分别为 ,
, ,若椭圆上第一象限的一个点A满足:直线
,若椭圆上第一象限的一个点A满足:直线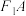 与直线
与直线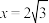 的交点为B,直线
的交点为B,直线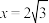 与x轴的交点为C,且射线
与x轴的交点为C,且射线 为∠ABC的角平分线,则
为∠ABC的角平分线,则 的面积为( )
的面积为( )
A.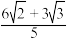 | B. |
C. | D.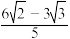 |
您最近一年使用:0次
2022-04-07更新
|
1898次组卷
|
6卷引用:广西柳州高级中学、南宁市第二中学2023届高三上学期9月联考数学(理)试题
广西柳州高级中学、南宁市第二中学2023届高三上学期9月联考数学(理)试题广西柳州高级中学、南宁市第二中学2023届高三上学期9月联考数学(文)试题云南师范大学附属中学2022届高三高考适应性月考卷(九)数学(理)试题(已下线)秘籍08 椭圆-备战2022年高考数学抢分秘籍(全国通用)(已下线)必刷卷01(文)-2022年高考数学考前信息必刷卷(全国乙卷)(已下线)专题3.17 圆锥曲线的方程全章综合测试卷-基础篇-2022-2023学年高二数学举一反三系列(人教A版2019选择性必修第一册)



