1 . 若两个椭圆的离心率相等,则称它们为“相似椭圆”.如图,在直角坐标系 中,已知椭圆
中,已知椭圆 :
: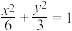 ,
, ,
, 分别为椭圆
分别为椭圆 的左、右顶点.椭圆
的左、右顶点.椭圆 以线段
以线段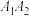 为短轴且与椭圆
为短轴且与椭圆 为“相似椭圆”.
为“相似椭圆”. 的方程;
的方程;
(2)设椭圆 的两个焦点
的两个焦点 ,
,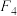 ,椭圆
,椭圆 的焦点为
的焦点为 、
、 ,求四边形
,求四边形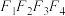 的面积;
的面积;
(3)设 为椭圆
为椭圆 上异于
上异于 ,
, 的任意一点,过
的任意一点,过 作
作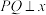 轴,垂足为
轴,垂足为 ,线段PQ交椭圆
,线段PQ交椭圆 于点
于点 .求证:
.求证: 为
为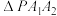 的垂心.
的垂心.
 中,已知椭圆
中,已知椭圆 :
: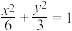 ,
, ,
, 分别为椭圆
分别为椭圆 的左、右顶点.椭圆
的左、右顶点.椭圆 以线段
以线段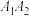 为短轴且与椭圆
为短轴且与椭圆 为“相似椭圆”.
为“相似椭圆”.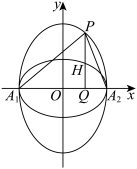
 的方程;
的方程;(2)设椭圆
 的两个焦点
的两个焦点 ,
,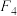 ,椭圆
,椭圆 的焦点为
的焦点为 、
、 ,求四边形
,求四边形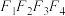 的面积;
的面积;(3)设
 为椭圆
为椭圆 上异于
上异于 ,
, 的任意一点,过
的任意一点,过 作
作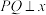 轴,垂足为
轴,垂足为 ,线段PQ交椭圆
,线段PQ交椭圆 于点
于点 .求证:
.求证: 为
为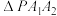 的垂心.
的垂心.
您最近一年使用:0次
名校
解题方法
2 . 已知椭圆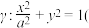 常数
常数 ,点
,点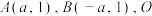 为坐标原点.
为坐标原点.
(1)求椭圆离心率的取值范围;
(2)若 是椭圆
是椭圆 上任意一点,
上任意一点, ,求
,求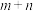 的取值范围;
的取值范围;
(3)设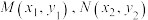 是椭圆
是椭圆 上的两个动点,满足
上的两个动点,满足 ,试探究
,试探究 的面积是否为定值,说明理由.
的面积是否为定值,说明理由.
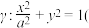 常数
常数 ,点
,点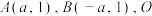 为坐标原点.
为坐标原点.(1)求椭圆离心率的取值范围;
(2)若
 是椭圆
是椭圆 上任意一点,
上任意一点, ,求
,求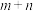 的取值范围;
的取值范围;(3)设
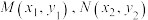 是椭圆
是椭圆 上的两个动点,满足
上的两个动点,满足 ,试探究
,试探究 的面积是否为定值,说明理由.
的面积是否为定值,说明理由.
您最近一年使用:0次
3 . 已知椭圆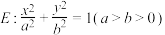 的离心率
的离心率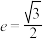 ,且
,且 上的点到点
上的点到点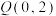 的距离的最大值为
的距离的最大值为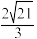 .
.
(1)求 的方程;
的方程;
(2)过 的直线
的直线 与
与 交于
交于 ,记
,记 关于
关于 轴的对称点为
轴的对称点为 .
.
①试证直线 恒过定点
恒过定点 ;
;
②若 在直线
在直线 上的投影分别为
上的投影分别为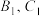 ,记
,记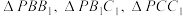 的面积分别为
的面积分别为 ,求
,求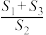 的取值范围.
的取值范围.
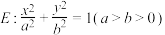 的离心率
的离心率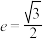 ,且
,且 上的点到点
上的点到点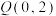 的距离的最大值为
的距离的最大值为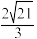 .
.(1)求
 的方程;
的方程;(2)过
 的直线
的直线 与
与 交于
交于 ,记
,记 关于
关于 轴的对称点为
轴的对称点为 .
.①试证直线
 恒过定点
恒过定点 ;
;②若
 在直线
在直线 上的投影分别为
上的投影分别为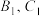 ,记
,记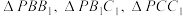 的面积分别为
的面积分别为 ,求
,求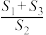 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
4 . 已知椭圆 的两个焦点是
的两个焦点是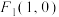 、
、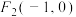 ,点
,点 在椭圆
在椭圆 上,且
上,且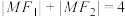 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)已知 为坐标原点,直线
为坐标原点,直线 与椭圆
与椭圆 交于
交于 、
、 两点,且
两点,且 ,证明:直线
,证明:直线 与圆
与圆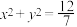 相切.
相切.
 的两个焦点是
的两个焦点是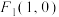 、
、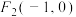 ,点
,点 在椭圆
在椭圆 上,且
上,且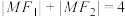 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)已知
 为坐标原点,直线
为坐标原点,直线 与椭圆
与椭圆 交于
交于 、
、 两点,且
两点,且 ,证明:直线
,证明:直线 与圆
与圆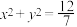 相切.
相切.
您最近一年使用:0次
名校
解题方法
5 . 已知椭圆 的左、右焦点别为
的左、右焦点别为 ,
, ,离心率为
,离心率为 ,过点
,过点 的动直线l交E于A,B两点,点A在x轴上方,且l不与x轴垂直,
的动直线l交E于A,B两点,点A在x轴上方,且l不与x轴垂直, 的周长为
的周长为 ,直线
,直线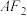 与E交于另一点C,直线
与E交于另一点C,直线 与E交于另一点D,点P为椭圆E的下顶点,如图.
与E交于另一点D,点P为椭圆E的下顶点,如图.
(2)证明:直线CD过定点.
 的左、右焦点别为
的左、右焦点别为 ,
, ,离心率为
,离心率为 ,过点
,过点 的动直线l交E于A,B两点,点A在x轴上方,且l不与x轴垂直,
的动直线l交E于A,B两点,点A在x轴上方,且l不与x轴垂直, 的周长为
的周长为 ,直线
,直线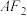 与E交于另一点C,直线
与E交于另一点C,直线 与E交于另一点D,点P为椭圆E的下顶点,如图.
与E交于另一点D,点P为椭圆E的下顶点,如图.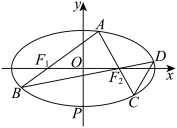
(2)证明:直线CD过定点.
您最近一年使用:0次
2024-09-03更新
|
702次组卷
|
4卷引用:四川省成都市外国语学校2023-2024学年高二下学期期末考试数学试题
四川省成都市外国语学校2023-2024学年高二下学期期末考试数学试题(已下线)模块二 专题2 解析几何中定值、定点、定直线问题【练】(高二期中压轴专项)(已下线)专题1 特殊探路 直接求解(经典好题母题)【练】河南省驻马店市新蔡县第一高级中学2024-2025学年高二上学期10月月考数学试题
名校
解题方法
6 . 在平面直角坐标系 中,抛物线
中,抛物线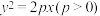 上一点A的横坐标为
上一点A的横坐标为 ,且点A到焦点F的距离为2.
,且点A到焦点F的距离为2.
(1)求抛物线的方程;
(2)点P在抛物线上,直线 与直线
与直线 交于Q点,过点F且平行于
交于Q点,过点F且平行于 的直线交抛物线于
的直线交抛物线于 两点,且
两点,且 ,求λ的值.
,求λ的值.
 中,抛物线
中,抛物线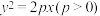 上一点A的横坐标为
上一点A的横坐标为 ,且点A到焦点F的距离为2.
,且点A到焦点F的距离为2.(1)求抛物线的方程;
(2)点P在抛物线上,直线
 与直线
与直线 交于Q点,过点F且平行于
交于Q点,过点F且平行于 的直线交抛物线于
的直线交抛物线于 两点,且
两点,且 ,求λ的值.
,求λ的值.
您最近一年使用:0次
名校
7 . 已知椭圆 的右焦点
的右焦点 坐标为
坐标为 ,两个焦点与短轴一个端点构成等边三角形.
,两个焦点与短轴一个端点构成等边三角形.
(1)求椭圆 的方程和离心率;
的方程和离心率;
(2)若过点 与点
与点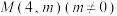 的直线
的直线 交椭圆于
交椭圆于 ,
, 两点,过点
两点,过点 且与直线
且与直线 平行的直线交
平行的直线交 轴于点
轴于点 ,直线
,直线 与直线
与直线 于点
于点 ,求
,求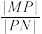 的值.
的值.
 的右焦点
的右焦点 坐标为
坐标为 ,两个焦点与短轴一个端点构成等边三角形.
,两个焦点与短轴一个端点构成等边三角形.(1)求椭圆
 的方程和离心率;
的方程和离心率;(2)若过点
 与点
与点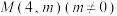 的直线
的直线 交椭圆于
交椭圆于 ,
, 两点,过点
两点,过点 且与直线
且与直线 平行的直线交
平行的直线交 轴于点
轴于点 ,直线
,直线 与直线
与直线 于点
于点 ,求
,求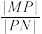 的值.
的值.
您最近一年使用:0次
名校
解题方法
8 . 已知双曲线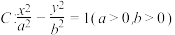 的右顶点
的右顶点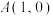 到
到 的一条渐近线的距离为
的一条渐近线的距离为 .
.
(1)求 的方程;
的方程;
(2)设过点 的直线交
的直线交 于
于 两点,过
两点,过 且垂直于
且垂直于 轴的直线与直线
轴的直线与直线 交于点
交于点 ,证明:以线段
,证明:以线段 的中点为圆心且过坐标原点的圆还过其他定点.
的中点为圆心且过坐标原点的圆还过其他定点.
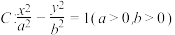 的右顶点
的右顶点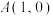 到
到 的一条渐近线的距离为
的一条渐近线的距离为 .
.(1)求
 的方程;
的方程;(2)设过点
 的直线交
的直线交 于
于 两点,过
两点,过 且垂直于
且垂直于 轴的直线与直线
轴的直线与直线 交于点
交于点 ,证明:以线段
,证明:以线段 的中点为圆心且过坐标原点的圆还过其他定点.
的中点为圆心且过坐标原点的圆还过其他定点.
您最近一年使用:0次
2024-08-17更新
|
226次组卷
|
5卷引用:山西省长治市2023-2024学年高二下学期6月期末数学试题
山西省长治市2023-2024学年高二下学期6月期末数学试题山东省济南市名校教研联盟2023-2024学年高二下学期6月月考数学试卷山西省阳泉市第一中学校2023-2024学年高二下学期期末测试数学试卷(已下线)模型10 圆锥曲线的定点、定值问题模型(第3章 圆锥曲线的方程)(已下线)专题1 特殊探路 直接求解(经典好题母题)【讲】
名校
解题方法
9 . 已知椭圆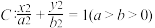 的离心率为
的离心率为 ,以椭圆
,以椭圆 的四个顶点为顶点的四边形的周长为8.
的四个顶点为顶点的四边形的周长为8.
(1)求椭圆 的方程;
的方程;
(2)设直线 是圆
是圆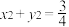 的一条切线,且直线
的一条切线,且直线 与椭圆
与椭圆 交于
交于 ,
, 两点,求
两点,求 的最大值.
的最大值.
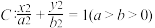 的离心率为
的离心率为 ,以椭圆
,以椭圆 的四个顶点为顶点的四边形的周长为8.
的四个顶点为顶点的四边形的周长为8.(1)求椭圆
 的方程;
的方程;(2)设直线
 是圆
是圆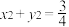 的一条切线,且直线
的一条切线,且直线 与椭圆
与椭圆 交于
交于 ,
, 两点,求
两点,求 的最大值.
的最大值.
您最近一年使用:0次
解题方法
10 . 设点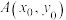 在曲线
在曲线 上,
上, 在曲线
在曲线 上,且满足
上,且满足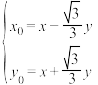 ,
,
(1)求 的方程;
的方程;
(2)点 在
在 上,过点
上,过点 的直线
的直线 与
与 的渐近线交于
的渐近线交于 两点,且
两点,且 是
是 的中点,求
的中点,求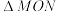 (
( 为坐标原点)的面积;
为坐标原点)的面积;
(3)利用双曲线定义证明:方程 表示的曲线是焦点在直线
表示的曲线是焦点在直线 上的双曲线.
上的双曲线.
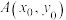 在曲线
在曲线 上,
上, 在曲线
在曲线 上,且满足
上,且满足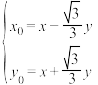 ,
,(1)求
 的方程;
的方程;(2)点
 在
在 上,过点
上,过点 的直线
的直线 与
与 的渐近线交于
的渐近线交于 两点,且
两点,且 是
是 的中点,求
的中点,求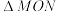 (
( 为坐标原点)的面积;
为坐标原点)的面积;(3)利用双曲线定义证明:方程
 表示的曲线是焦点在直线
表示的曲线是焦点在直线 上的双曲线.
上的双曲线.
您最近一年使用:0次



