解题方法
1 . 已知双曲线 的离心率为
的离心率为 ,右焦点到双曲线C的一条渐近线的距离为1,两动点A,B在双曲线C上,线段AB的中点为
,右焦点到双曲线C的一条渐近线的距离为1,两动点A,B在双曲线C上,线段AB的中点为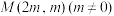 .
.
(1)求双曲线C的标准方程;
(2)O为坐标原点,若 的面积为
的面积为 ,求直线AB的方程.
,求直线AB的方程.
 的离心率为
的离心率为 ,右焦点到双曲线C的一条渐近线的距离为1,两动点A,B在双曲线C上,线段AB的中点为
,右焦点到双曲线C的一条渐近线的距离为1,两动点A,B在双曲线C上,线段AB的中点为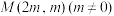 .
.(1)求双曲线C的标准方程;
(2)O为坐标原点,若
 的面积为
的面积为 ,求直线AB的方程.
,求直线AB的方程.
您最近一年使用:0次
2024高二·全国·专题练习
解题方法
2 . 已知椭圆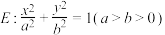 的离心率
的离心率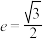 ,且
,且 上的点到
上的点到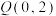 的距离的最大值为
的距离的最大值为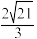 .
.
(1)求 的方程;
的方程;
(2)过 的直线
的直线 与
与 交于
交于 ,记
,记 关于
关于 轴的对称点为
轴的对称点为 .证明:直线
.证明:直线 恒过定点
恒过定点 ;
;
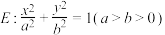 的离心率
的离心率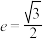 ,且
,且 上的点到
上的点到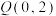 的距离的最大值为
的距离的最大值为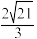 .
.(1)求
 的方程;
的方程;(2)过
 的直线
的直线 与
与 交于
交于 ,记
,记 关于
关于 轴的对称点为
轴的对称点为 .证明:直线
.证明:直线 恒过定点
恒过定点 ;
;
您最近一年使用:0次
3 . 已知椭圆 的左、右焦点分别是
的左、右焦点分别是 ,上顶点为
,上顶点为 ,其长轴长是短轴长的2倍,
,其长轴长是短轴长的2倍, 是
是 上任意一点,
上任意一点, 的最大值为
的最大值为 .
.
(1)求椭圆 的方程;
的方程;
(2)过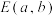 作一直线与
作一直线与 交于
交于 两点,直线
两点,直线 与
与 轴分别交于点
轴分别交于点 ,求证:
,求证: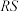 的中点是定点.
的中点是定点.
 的左、右焦点分别是
的左、右焦点分别是 ,上顶点为
,上顶点为 ,其长轴长是短轴长的2倍,
,其长轴长是短轴长的2倍, 是
是 上任意一点,
上任意一点, 的最大值为
的最大值为 .
.(1)求椭圆
 的方程;
的方程;(2)过
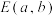 作一直线与
作一直线与 交于
交于 两点,直线
两点,直线 与
与 轴分别交于点
轴分别交于点 ,求证:
,求证: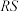 的中点是定点.
的中点是定点.
您最近一年使用:0次
解题方法
4 . 已知抛物线Γ: ,A为第一象限内Γ上的一点,设A的纵坐标为
,A为第一象限内Γ上的一点,设A的纵坐标为 .
.
(1)若点A到Γ的准线的距离为3,求a的值;
(2)若 ,B为x轴上的一点,且线段AB的中点在Γ上,求点B的坐标及原点O到直线AB的距离;
,B为x轴上的一点,且线段AB的中点在Γ上,求点B的坐标及原点O到直线AB的距离;
(3)设直线l: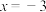 ,P是第一象限内Γ上异于A的动点,直线AP与直线l交于点Q,点H为点P在直线l上的投影,若点A满足性质“当点P变化时,
,P是第一象限内Γ上异于A的动点,直线AP与直线l交于点Q,点H为点P在直线l上的投影,若点A满足性质“当点P变化时, 恒成立”,求a的取值范围.
恒成立”,求a的取值范围.
 ,A为第一象限内Γ上的一点,设A的纵坐标为
,A为第一象限内Γ上的一点,设A的纵坐标为 .
.(1)若点A到Γ的准线的距离为3,求a的值;
(2)若
 ,B为x轴上的一点,且线段AB的中点在Γ上,求点B的坐标及原点O到直线AB的距离;
,B为x轴上的一点,且线段AB的中点在Γ上,求点B的坐标及原点O到直线AB的距离;(3)设直线l:
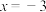 ,P是第一象限内Γ上异于A的动点,直线AP与直线l交于点Q,点H为点P在直线l上的投影,若点A满足性质“当点P变化时,
,P是第一象限内Γ上异于A的动点,直线AP与直线l交于点Q,点H为点P在直线l上的投影,若点A满足性质“当点P变化时, 恒成立”,求a的取值范围.
恒成立”,求a的取值范围.
您最近一年使用:0次
名校
解题方法
5 . 已知A,B分别是双曲线 的左、右顶点,P是C上异于A,B的一点,直线PA,PB的斜率分别为
的左、右顶点,P是C上异于A,B的一点,直线PA,PB的斜率分别为 ,且
,且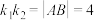 .
.
(1)求双曲线C的方程;
(2)已知过点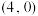 的直线
的直线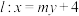 ,交C的左,右两支于D,E两点(异于A,B).
,交C的左,右两支于D,E两点(异于A,B).
(i)求m的取值范围;
(ii)设直线AD与直线BE交于点Q,求证:点Q在定直线上.
 的左、右顶点,P是C上异于A,B的一点,直线PA,PB的斜率分别为
的左、右顶点,P是C上异于A,B的一点,直线PA,PB的斜率分别为 ,且
,且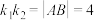 .
.(1)求双曲线C的方程;
(2)已知过点
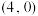 的直线
的直线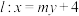 ,交C的左,右两支于D,E两点(异于A,B).
,交C的左,右两支于D,E两点(异于A,B).(i)求m的取值范围;
(ii)设直线AD与直线BE交于点Q,求证:点Q在定直线上.
您最近一年使用:0次
2024-06-10更新
|
566次组卷
|
4卷引用:黑龙江省大庆市大庆中学2023-2024学年高二下学期5月期中考试数学试题
黑龙江省大庆市大庆中学2023-2024学年高二下学期5月期中考试数学试题(已下线)专题6 圆锥曲线三定义及其应用【讲】(已下线)重难点突破16 圆锥曲线中的定点、定值问题(十二大题型)-2考点考题点点通——第三章圆锥曲线的方程
名校
解题方法
6 . 已知抛物线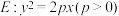 与双曲线
与双曲线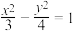 的渐近线在第一象限的交点为Q,且Q点的横坐标为3.
的渐近线在第一象限的交点为Q,且Q点的横坐标为3.
(1)求抛物线E的方程;
(2)过点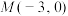 的直线l与抛物线E相交于
的直线l与抛物线E相交于 两点,B关于x轴的对称点为
两点,B关于x轴的对称点为 ,求证:直线
,求证:直线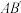 必过定点.
必过定点.
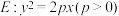 与双曲线
与双曲线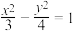 的渐近线在第一象限的交点为Q,且Q点的横坐标为3.
的渐近线在第一象限的交点为Q,且Q点的横坐标为3.(1)求抛物线E的方程;
(2)过点
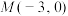 的直线l与抛物线E相交于
的直线l与抛物线E相交于 两点,B关于x轴的对称点为
两点,B关于x轴的对称点为 ,求证:直线
,求证:直线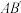 必过定点.
必过定点.
您最近一年使用:0次
名校
解题方法
7 . 在平面直角坐标系 中,动点
中,动点 在抛物线
在抛物线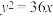 上运动,点
上运动,点 在
在 轴上的射影为
轴上的射影为 ,动点
,动点 满足
满足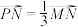 .
.
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)过点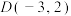 作直线与曲线
作直线与曲线 顺次交于
顺次交于 、
、 两点,过点
两点,过点 作斜率为1的直线与曲线
作斜率为1的直线与曲线 的另一个交点为点
的另一个交点为点 ,求证:直线
,求证:直线 过定点.
过定点.
 中,动点
中,动点 在抛物线
在抛物线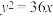 上运动,点
上运动,点 在
在 轴上的射影为
轴上的射影为 ,动点
,动点 满足
满足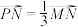 .
.(1)求动点
 的轨迹
的轨迹 的方程;
的方程;(2)过点
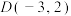 作直线与曲线
作直线与曲线 顺次交于
顺次交于 、
、 两点,过点
两点,过点 作斜率为1的直线与曲线
作斜率为1的直线与曲线 的另一个交点为点
的另一个交点为点 ,求证:直线
,求证:直线 过定点.
过定点.
您最近一年使用:0次
2024-09-01更新
|
427次组卷
|
3卷引用:广西南宁市第二中学2023-2024学年高二上学期11月期中数学试题
名校
解题方法
8 . 在平面直角坐标系 中,双曲线
中,双曲线 的左顶点到右焦点的距离是3,且
的左顶点到右焦点的距离是3,且 的离心率是2.
的离心率是2.
(1)求双曲线 的标准方程;
的标准方程;
(2)点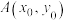 是
是 上位于第一象限的一点,点
上位于第一象限的一点,点 关于原点
关于原点 对称,点
对称,点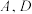 关于
关于 轴对称.延长
轴对称.延长 至
至 使得
使得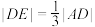 ,且直线
,且直线 和
和 的另一个交点
的另一个交点 位于第二象限中.
位于第二象限中.
(ⅰ)求 的取值范围,并判断
的取值范围,并判断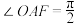 是否成立?
是否成立?
(ⅱ)证明: 不可能是
不可能是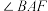 的三等分线.
的三等分线.
 中,双曲线
中,双曲线 的左顶点到右焦点的距离是3,且
的左顶点到右焦点的距离是3,且 的离心率是2.
的离心率是2.(1)求双曲线
 的标准方程;
的标准方程;(2)点
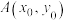 是
是 上位于第一象限的一点,点
上位于第一象限的一点,点 关于原点
关于原点 对称,点
对称,点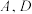 关于
关于 轴对称.延长
轴对称.延长 至
至 使得
使得 ,且直线
,且直线 和
和 的另一个交点
的另一个交点 位于第二象限中.
位于第二象限中.(ⅰ)求
 的取值范围,并判断
的取值范围,并判断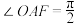 是否成立?
是否成立?(ⅱ)证明:
 不可能是
不可能是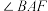 的三等分线.
的三等分线.
您最近一年使用:0次
名校
解题方法
9 . 定义:若椭圆 上的两个点
上的两个点 ,
, 满足
满足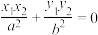 ,则称A,B为该椭圆的一个“共轭点对”,记作
,则称A,B为该椭圆的一个“共轭点对”,记作 .已知椭圆C:
.已知椭圆C: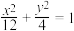 上一点
上一点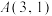 .
.
(1)求“共轭点对” 中点B所在直线l的方程.
中点B所在直线l的方程.
(2)设O为坐标原点,点P,Q在椭圆C上,且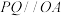 ,(1)中的直线l与椭圆C交于两点
,(1)中的直线l与椭圆C交于两点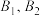 .
.
①求点 ,
, 的坐标;
的坐标;
②设四点 ,P,
,P, ,Q在椭圆C上逆时针排列,证明:四边形
,Q在椭圆C上逆时针排列,证明:四边形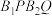 的面积小于
的面积小于 .
.
 上的两个点
上的两个点 ,
, 满足
满足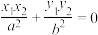 ,则称A,B为该椭圆的一个“共轭点对”,记作
,则称A,B为该椭圆的一个“共轭点对”,记作 .已知椭圆C:
.已知椭圆C: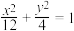 上一点
上一点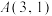 .
.(1)求“共轭点对”
 中点B所在直线l的方程.
中点B所在直线l的方程.(2)设O为坐标原点,点P,Q在椭圆C上,且
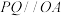 ,(1)中的直线l与椭圆C交于两点
,(1)中的直线l与椭圆C交于两点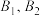 .
.①求点
 ,
, 的坐标;
的坐标;②设四点
 ,P,
,P, ,Q在椭圆C上逆时针排列,证明:四边形
,Q在椭圆C上逆时针排列,证明:四边形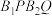 的面积小于
的面积小于 .
.
您最近一年使用:0次
2023-08-13更新
|
946次组卷
|
4卷引用:贵州省2024届高三上学期入学考试数学试题
10 . 已知动点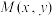 与定点
与定点 的距离和
的距离和 到定直线
到定直线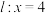 的距离的比是常数
的距离的比是常数 .
.
(1)求动点 的轨迹方程,并说明轨迹即曲线
的轨迹方程,并说明轨迹即曲线 的形状.
的形状.
(2)过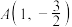 作两直线与抛物线
作两直线与抛物线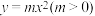 相切,且分别与曲线
相切,且分别与曲线 交于
交于 ,
, 两点,直线
两点,直线 ,
, 的斜率分别为
的斜率分别为 ,
, .
.
①求证: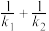 为定值;
为定值;
②试问直线 是否过定点,若是,求出定点坐标;若不是,说明理由.
是否过定点,若是,求出定点坐标;若不是,说明理由.
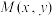 与定点
与定点 的距离和
的距离和 到定直线
到定直线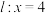 的距离的比是常数
的距离的比是常数 .
.(1)求动点
 的轨迹方程,并说明轨迹即曲线
的轨迹方程,并说明轨迹即曲线 的形状.
的形状.(2)过
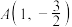 作两直线与抛物线
作两直线与抛物线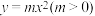 相切,且分别与曲线
相切,且分别与曲线 交于
交于 ,
, 两点,直线
两点,直线 ,
, 的斜率分别为
的斜率分别为 ,
, .
.①求证:
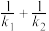 为定值;
为定值;②试问直线
 是否过定点,若是,求出定点坐标;若不是,说明理由.
是否过定点,若是,求出定点坐标;若不是,说明理由.
您最近一年使用:0次
2023-12-27更新
|
1318次组卷
|
6卷引用:江苏省无锡市第六高级中学2024届高三上学期12月教学质量调研数学试题
江苏省无锡市第六高级中学2024届高三上学期12月教学质量调研数学试题(已下线)模块五 专题5 期末全真模拟(拔高卷1)期末终极研习室(高二人教A版)四川省泸州市泸县第一中学2023-2024学年高二上学期期末数学试题(已下线)高二上学期数学期末模拟卷(二)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)江西省丰城市第二中学2023-2024学年高二下学期4月月考数学试题湖南省永州市第四中学2025届高三上学期第二次模拟考试数学试卷



