解题方法
1 . 在平面直角坐标系xOy中,方程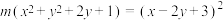 表示椭圆,求m的取值范围.
表示椭圆,求m的取值范围.
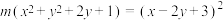 表示椭圆,求m的取值范围.
表示椭圆,求m的取值范围.
您最近一年使用:0次
解题方法
2 . 已知A是抛物线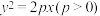 上一点(异于原点),斜率为
上一点(异于原点),斜率为 的直线
的直线 与抛物线恰有一个公共点A(
与抛物线恰有一个公共点A( 与x轴不平行).
与x轴不平行).
(1)当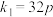 时,求点A的纵坐标;
时,求点A的纵坐标;
(2)斜率为 的直线
的直线 与抛物线交于B,C两点,且
与抛物线交于B,C两点,且 是正三角形,求
是正三角形,求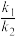 的取值范围.
的取值范围.
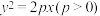 上一点(异于原点),斜率为
上一点(异于原点),斜率为 的直线
的直线 与抛物线恰有一个公共点A(
与抛物线恰有一个公共点A( 与x轴不平行).
与x轴不平行).(1)当
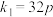 时,求点A的纵坐标;
时,求点A的纵坐标;(2)斜率为
 的直线
的直线 与抛物线交于B,C两点,且
与抛物线交于B,C两点,且 是正三角形,求
是正三角形,求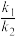 的取值范围.
的取值范围.
您最近一年使用:0次
2024-02-28更新
|
327次组卷
|
2卷引用:2024年集英苑冬季竞赛高中数学试题
3 . 17世纪德国天文学家约翰内斯·开普勒提出描述行星运动的三大基本定律:
(a)行星绕太阳运动的轨道为椭圆(圆可视为特殊的椭圆),太阳位于椭圆的一个焦点上,所有行星的轨道可近似看成在同一平面内;
(b)行星在其椭圆轨道上的相等时间内,与太阳连线所扫过的面积相等.
(c)行星的公转周期的平方与它们的椭圆轨道长轴的立方成正比.
开普勒三定律为我们理解行星运动提供了重要的基础,并且被广泛应用于天体力学和行星轨道计算中.设a,b, ,地球、太阳、火星均可视为点,太阳位于
,地球、太阳、火星均可视为点,太阳位于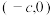 ,地球的公转轨道可近似看成圆
,地球的公转轨道可近似看成圆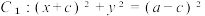 ,火星的公转轨道可近似看成圆
,火星的公转轨道可近似看成圆 ,且火星的公转周期约为地球公转周期的1.882倍.霍曼转移轨道E是以太阳所在位置为其中一个焦点,并且与
,且火星的公转周期约为地球公转周期的1.882倍.霍曼转移轨道E是以太阳所在位置为其中一个焦点,并且与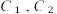 均相切的椭圆.2020年,我国自主研制的火星探测器天问一号从地球发射,经霍曼转移轨道到达火星,如下图所示.
均相切的椭圆.2020年,我国自主研制的火星探测器天问一号从地球发射,经霍曼转移轨道到达火星,如下图所示.
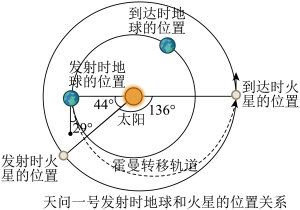
(1)计算霍曼转移轨道E的离心率.(参考数据: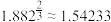 ,计算结果保留两位小数)
,计算结果保留两位小数)
(2)设天问一号位于E上的一点P,当P不在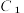 上时,
上时,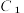 上存在依赖于P的两点A,B,使得
上存在依赖于P的两点A,B,使得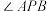 为观测地球的最大视角(即地球不可能位于该角的外部),问:轨道平面内是否存在定圆
为观测地球的最大视角(即地球不可能位于该角的外部),问:轨道平面内是否存在定圆 ,使得直线AB恒与
,使得直线AB恒与 相切?证明你的结论.
相切?证明你的结论.
(a)行星绕太阳运动的轨道为椭圆(圆可视为特殊的椭圆),太阳位于椭圆的一个焦点上,所有行星的轨道可近似看成在同一平面内;
(b)行星在其椭圆轨道上的相等时间内,与太阳连线所扫过的面积相等.
(c)行星的公转周期的平方与它们的椭圆轨道长轴的立方成正比.
开普勒三定律为我们理解行星运动提供了重要的基础,并且被广泛应用于天体力学和行星轨道计算中.设a,b,
 ,地球、太阳、火星均可视为点,太阳位于
,地球、太阳、火星均可视为点,太阳位于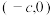 ,地球的公转轨道可近似看成圆
,地球的公转轨道可近似看成圆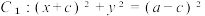 ,火星的公转轨道可近似看成圆
,火星的公转轨道可近似看成圆 ,且火星的公转周期约为地球公转周期的1.882倍.霍曼转移轨道E是以太阳所在位置为其中一个焦点,并且与
,且火星的公转周期约为地球公转周期的1.882倍.霍曼转移轨道E是以太阳所在位置为其中一个焦点,并且与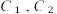 均相切的椭圆.2020年,我国自主研制的火星探测器天问一号从地球发射,经霍曼转移轨道到达火星,如下图所示.
均相切的椭圆.2020年,我国自主研制的火星探测器天问一号从地球发射,经霍曼转移轨道到达火星,如下图所示.
(1)计算霍曼转移轨道E的离心率.(参考数据:
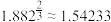 ,计算结果保留两位小数)
,计算结果保留两位小数)(2)设天问一号位于E上的一点P,当P不在
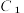 上时,
上时,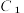 上存在依赖于P的两点A,B,使得
上存在依赖于P的两点A,B,使得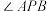 为观测地球的最大视角(即地球不可能位于该角的外部),问:轨道平面内是否存在定圆
为观测地球的最大视角(即地球不可能位于该角的外部),问:轨道平面内是否存在定圆 ,使得直线AB恒与
,使得直线AB恒与 相切?证明你的结论.
相切?证明你的结论.
您最近一年使用:0次
解题方法
4 . 已知点 ,
,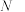 、
、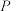 两点分别在
两点分别在 轴、
轴、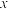 轴上运动,且满足
轴上运动,且满足 ,
,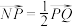 .
.
(1)求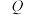 的轨迹方程;
的轨迹方程;
(2)若一正方形的三个顶点在点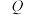 的轨迹上,求其面积的最小值.
的轨迹上,求其面积的最小值.
 ,
,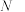 、
、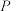 两点分别在
两点分别在 轴、
轴、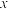 轴上运动,且满足
轴上运动,且满足 ,
,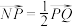 .
.(1)求
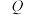 的轨迹方程;
的轨迹方程;(2)若一正方形的三个顶点在点
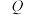 的轨迹上,求其面积的最小值.
的轨迹上,求其面积的最小值.
您最近一年使用:0次
名校
解题方法
5 . 在平面直角坐标系 中,已知抛物线
中,已知抛物线 :
: ,
, 为其焦点,点
为其焦点,点 的坐标为
的坐标为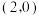 ,设
,设 为抛物线
为抛物线 上异于顶点的动点,直线
上异于顶点的动点,直线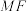 交抛物线
交抛物线 于另一点
于另一点 ,连接
,连接 ,
,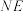 并延长分别交抛物线
并延长分别交抛物线 于点
于点 .
.
(1)当 轴时,求直线
轴时,求直线 与
与 轴交点的坐标;
轴交点的坐标;
(2)当直线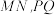 的斜率存在且分别记为
的斜率存在且分别记为 ,
, 时,求证:
时,求证: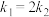 .
.
 中,已知抛物线
中,已知抛物线 :
: ,
, 为其焦点,点
为其焦点,点 的坐标为
的坐标为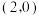 ,设
,设 为抛物线
为抛物线 上异于顶点的动点,直线
上异于顶点的动点,直线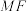 交抛物线
交抛物线 于另一点
于另一点 ,连接
,连接 ,
,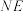 并延长分别交抛物线
并延长分别交抛物线 于点
于点 .
.(1)当
 轴时,求直线
轴时,求直线 与
与 轴交点的坐标;
轴交点的坐标;(2)当直线
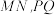 的斜率存在且分别记为
的斜率存在且分别记为 ,
, 时,求证:
时,求证: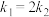 .
.
您最近一年使用:0次
2023-12-27更新
|
815次组卷
|
6卷引用:福建省莆田市仙游第一中学等五校联考2022-2023学年高二上学期期末数学试题
福建省莆田市仙游第一中学等五校联考2022-2023学年高二上学期期末数学试题(已下线)每日一题 第22题 非对称问题 凑结构代换(高二)山东省泰安市新泰市第一中学东校2023-2024学年高二上学期冬季学科竞赛数学试题(已下线)专题03 圆锥曲线题型全归纳(九大考点)-【寒假自学课】2024年高二数学寒假提升学与练(人教A版2019)(已下线)第7讲:圆锥曲线的模型【练】(已下线)第5讲:定点、定值、定直线问题【练】
名校
解题方法
6 . 已知双曲线 的左、右焦点分别为
的左、右焦点分别为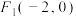 ,
,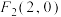 ,点
,点 在双曲线
在双曲线 上.
上.
(1)求 的方程;
的方程;
(2)过 作两条相互垂直的直线
作两条相互垂直的直线 和
和 ,与
,与 的右支分别交
的右支分别交 ,
, 两点和
两点和 ,
, 两点,求四边形
两点,求四边形 面积的最小值.
面积的最小值.
 的左、右焦点分别为
的左、右焦点分别为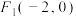 ,
,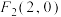 ,点
,点 在双曲线
在双曲线 上.
上.(1)求
 的方程;
的方程;(2)过
 作两条相互垂直的直线
作两条相互垂直的直线 和
和 ,与
,与 的右支分别交
的右支分别交 ,
, 两点和
两点和 ,
, 两点,求四边形
两点,求四边形 面积的最小值.
面积的最小值.
您最近一年使用:0次
2023-11-16更新
|
1725次组卷
|
11卷引用:湖南省长沙市雅礼中学2023-2024学年高二上学期期中数学试题
湖南省长沙市雅礼中学2023-2024学年高二上学期期中数学试题湖南省长沙市雨花区雅礼教育集团2023-2024学年高二上学期期中数学试题广东省肇庆市第一中学2023-2024学年高二上学期学科能力竞赛数学试题浙江省温州市温州中学2023-2024学年高二上学期12月月考数学试题(已下线)3.2.2 双曲线的几何性质(8大题型)-【题型分类归纳】2023-2024学年高二数学同步讲与练(苏教版2019选择性必修第一册)(已下线)第3章:圆锥曲线与方程章末重点题型复习-【题型分类归纳】2023-2024学年高二数学同步讲与练(苏教版2019选择性必修第一册)(已下线)第三章:圆锥曲线的方程章末重点题型复习-【题型分类归纳】2023-2024学年高二数学同步讲与练(人教A版2019选择性必修第一册)(已下线)第7讲:圆锥曲线的模型【练】(已下线)通关练16 双曲线13考点精练(100题)- 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教A版2019选择性必修第一册)(已下线)专题26 直线与圆锥曲线的位置关系5种常见考法归类 - 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教B版2019选择性必修第一册)(已下线)重组6 高二期中真题重组卷(湖南卷)B提升卷
名校
解题方法
7 . 已知点 ,点
,点 和点
和点 为椭圆
为椭圆 上不同的三个点.当点
上不同的三个点.当点 ,点B和点C为椭圆的顶点时,△ABC恰好是边长为2的等边三角形.
,点B和点C为椭圆的顶点时,△ABC恰好是边长为2的等边三角形.
(1)求椭圆 标准方程;
标准方程;
(2)若 为原点,且满足
为原点,且满足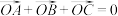 ,求
,求 的面积.
的面积.
 ,点
,点 和点
和点 为椭圆
为椭圆 上不同的三个点.当点
上不同的三个点.当点 ,点B和点C为椭圆的顶点时,△ABC恰好是边长为2的等边三角形.
,点B和点C为椭圆的顶点时,△ABC恰好是边长为2的等边三角形.(1)求椭圆
 标准方程;
标准方程;(2)若
 为原点,且满足
为原点,且满足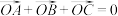 ,求
,求 的面积.
的面积.
您最近一年使用:0次
2023-03-30更新
|
3238次组卷
|
7卷引用:广东省部分学校2023届高三下学期3月模拟数学试题
广东省部分学校2023届高三下学期3月模拟数学试题广东省2023届高考一模数学试题专题20平面解析几何(解答题)(已下线)第84练 计算速度训练4广东省肇庆市第一中学2023-2024学年高二上学期学科能力竞赛数学试题(已下线)第7讲:圆锥曲线的模型【练】专题08椭圆问题(解答题)
8 . 设点 在抛物线
在抛物线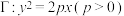 上,
上, 的焦点为
的焦点为 .
. 、
、 为过
为过 的两条倾斜角互补的直线,且
的两条倾斜角互补的直线,且 、
、 与
与 的另一交点分别为
的另一交点分别为 、
、 .已知直线
.已知直线 的斜率为
的斜率为 .
.
(1)求直线 的斜率;
的斜率;
(2)记 、
、 与
与 轴的交点分别为
轴的交点分别为 、
、 .设
.设 和
和 分别为
分别为 和
和 的面积,当
的面积,当 时,求
时,求 的取值范围.
的取值范围.
 在抛物线
在抛物线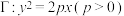 上,
上, 的焦点为
的焦点为 .
. 、
、 为过
为过 的两条倾斜角互补的直线,且
的两条倾斜角互补的直线,且 、
、 与
与 的另一交点分别为
的另一交点分别为 、
、 .已知直线
.已知直线 的斜率为
的斜率为 .
.(1)求直线
 的斜率;
的斜率;(2)记
 、
、 与
与 轴的交点分别为
轴的交点分别为 、
、 .设
.设 和
和 分别为
分别为 和
和 的面积,当
的面积,当 时,求
时,求 的取值范围.
的取值范围.
您最近一年使用:0次
9 . 已知椭圆 .
.
(1)若过椭圆的一个焦点引两条互相垂直的弦 、
、 .求证:
.求证: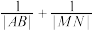 是定值;
是定值;
(2)若 、
、 在椭圆上且
在椭圆上且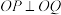 .求证:
.求证: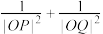 是定值.
是定值.
 .
.(1)若过椭圆的一个焦点引两条互相垂直的弦
 、
、 .求证:
.求证: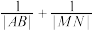 是定值;
是定值;(2)若
 、
、 在椭圆上且
在椭圆上且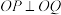 .求证:
.求证: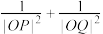 是定值.
是定值.
您最近一年使用:0次
2022-09-07更新
|
794次组卷
|
5卷引用:沪教版(2020) 选修第一册 精准辅导 第2章 2.2(3) 椭圆的性质(第2课时)
沪教版(2020) 选修第一册 精准辅导 第2章 2.2(3) 椭圆的性质(第2课时)江西省吉安市永丰县永丰中学2022-2023学年高二上学期期末考试数学试题(A)(已下线)第26讲 圆锥曲线中定值问题(1)安徽省安庆市田家炳中学2022-2023学年高二下学期第二届“校长杯”竞赛数学试题(已下线)第5讲:定点、定值、定直线问题【练】
10 . 已知抛物线 ,过其焦点
,过其焦点 作两条相互垂直且不平行于
作两条相互垂直且不平行于 轴的直线,分别交抛物线
轴的直线,分别交抛物线 于点
于点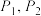 和点
和点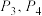 ,线段
,线段 的中点分别记为
的中点分别记为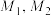 .
.
(1)求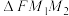 面积的最小值;
面积的最小值;
(2)求线段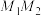 的中点
的中点 满足的方程.
满足的方程.
 ,过其焦点
,过其焦点 作两条相互垂直且不平行于
作两条相互垂直且不平行于 轴的直线,分别交抛物线
轴的直线,分别交抛物线 于点
于点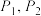 和点
和点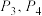 ,线段
,线段 的中点分别记为
的中点分别记为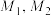 .
.(1)求
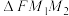 面积的最小值;
面积的最小值;(2)求线段
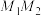 的中点
的中点 满足的方程.
满足的方程.
您最近一年使用:0次



