1 . 一医疗团队为研究某地的一种地方性疾病与当地居民的卫生习惯(卫生习惯分为良好和不够良好两类)的关系,在已患该疾病的病例中随机调查了100例(称为病例组),同时在未患该疾病的人群中随机调查了100人(称为对照组),得到如下数据:
(1)能否有99%的把握认为患该疾病群体与未患该疾病群体的卫生习惯有差异?
(2)从该地的人群中任选一人,A表示事件“选到的人卫生习惯不够良好”,B表示事件“选到的人患有该疾病”. 与
与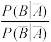 的比值是卫生习惯不够良好对患该疾病风险程度的一项度量指标,记该指标为R.
的比值是卫生习惯不够良好对患该疾病风险程度的一项度量指标,记该指标为R.
(ⅰ)证明: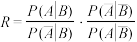 ;
;
(ⅱ)利用该调查数据,给出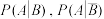 的估计值,并利用(ⅰ)的结果给出R的估计值.
的估计值,并利用(ⅰ)的结果给出R的估计值.
附 ,
,
不够良好 | 良好 | |
病例组 | 40 | 60 |
对照组 | 10 | 90 |
(2)从该地的人群中任选一人,A表示事件“选到的人卫生习惯不够良好”,B表示事件“选到的人患有该疾病”.
 与
与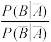 的比值是卫生习惯不够良好对患该疾病风险程度的一项度量指标,记该指标为R.
的比值是卫生习惯不够良好对患该疾病风险程度的一项度量指标,记该指标为R.(ⅰ)证明:
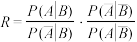 ;
;(ⅱ)利用该调查数据,给出
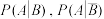 的估计值,并利用(ⅰ)的结果给出R的估计值.
的估计值,并利用(ⅰ)的结果给出R的估计值.附
 ,
,
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
您最近一年使用:0次
2022-06-07更新
|
53466次组卷
|
52卷引用:辽宁新高考联盟(点石联考)2023-2024学年高二下学期3月联合考试数学试题
辽宁新高考联盟(点石联考)2023-2024学年高二下学期3月联合考试数学试题2022年新高考全国I卷数学真题(已下线)2022年全国新高考Ⅰ卷数学试题变式题13-16题(已下线)第8讲 计数原理与概率统计(2021-2022年高考真题)(已下线)专题13 概率统计解答题(已下线)专题14 概率统计解答题-1(已下线)6.2 古典概型及条件概率(精练)(已下线)第03讲 成对数据的统计分析 (精讲)(已下线)第09讲 高考中的概率与统计 (精讲)-2(已下线)2022年全国新高考Ⅰ卷数学试题变式题20-22题(已下线)考向40 事件的相互独立性、条件概率与全概率公式(七大经典题型)-2(已下线)考向38统计与统计案例(重点)-1(已下线)考向44事件的独立性与条件概率(重点)-1广东省深圳市福田区福田中学2023届高三上学期第一次月考数学试题(已下线)专题1 2022高考命题分析与专家整体解读(已下线)专题9 2022年高考“概率与统计”专题命题分析安徽省教育厅2023届高三老高考新课标题型示例数学试题(已下线)专题10 概率与统计的综合运用(精讲精练)-1(已下线)专题3 解答题题型(已下线)第八章 成对数据的统计分析 (单元测)(已下线)模块三 专题6 概率与统计(已下线)重组卷02(已下线)重组卷02(已下线)重组卷04(已下线)押新高考第19题 概率统计(已下线)专题9-1 概率与统计及分布列归类(理)(讲+练)-1专题08计数原理与概率统计(成品)专题08计数原理与概率统计(添加试题分类成品)(已下线)拓展一:近八年统计案例高考真题分类汇编 -【帮课堂】2022-2023学年高二数学同步精品讲义(人教A版2019选择性必修第三册)(已下线)第8章 成对数据的统计分析(基础、常考)分类专项训练-【满分全攻略】2022-2023学年高二数学下学期核心考点+重难点讲练与测试(沪教版2020选修一+选修二)福建省龙岩市上杭县第一中学2024届高三上学期10月月考数学试题(已下线)第06讲 事件的相互独立性、条件概率与全概率公式(练习)(已下线)第02讲 成对数据的统计分析(练习)(已下线)考点17 列联表与独立性检验 2024届高考数学考点总动员(已下线)专题16 统计(已下线)第七章 统计案例(单元综合检测卷)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)(已下线)第2讲:条件概率与全概率公式的应用【练】(已下线)【类题归纳】先验后验 条件概率(已下线)专题05 高考概统大题真题精练(已下线)专题21 概率与统计的综合运用(13大核心考点)(讲义)(已下线)专题11 统计与概率(解密讲义)(已下线)专题09 计数原理与随机变量及分布列(讲义)上海市进才中学2023-2024学年高三下学期3月月考数学试卷上海市宝山区吴淞中学2024届高三下学期3月月考数学试题(已下线)【一题多变】 分类变量 独立检验(已下线)专题10.1 概率与统计的综合运用【十一大题型】(举一反三)(新高考专用)-2(已下线)8.3.1分类变量与列联表+8.3.2独立性检验 第三课 知识扩展延伸(已下线)8.5 二项分布、超几何分布与正态分布(高考真题素材之十年高考)黑龙江省齐齐哈尔市2024届高三下学期联合考试模拟预测数学试题(已下线)专题25 概率统计解答题(理科)-1(已下线)专题25 概率统计解答题(文科)(已下线)专题4 考前押题大猜想16-20
真题
名校
2 . 某地经过多年的环境治理,已将荒山改造成了绿水青山.为估计一林区某种树木的总材积量,随机选取了10棵这种树木,测量每棵树的根部横截面积(单位: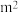 )和材积量(单位:
)和材积量(单位: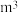 ),得到如下数据:
),得到如下数据:
并计算得 .
.
(1)估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量;
(2)求该林区这种树木的根部横截面积与材积量的样本相关系数(精确到0.01);
(3)现测量了该林区所有这种树木的根部横截面积,并得到所有这种树木的根部横截面积总和为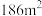 .已知树木的材积量与其根部横截面积近似成正比.利用以上数据给出该林区这种树木的总材积量的估计值.
.已知树木的材积量与其根部横截面积近似成正比.利用以上数据给出该林区这种树木的总材积量的估计值.
附:相关系数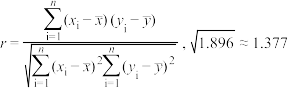 .
.
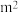 )和材积量(单位:
)和材积量(单位: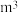 ),得到如下数据:
),得到如下数据:| 样本号i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 总和 |
根部横截面积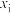 | 0.04 | 0.06 | 0.04 | 0.08 | 0.08 | 0.05 | 0.05 | 0.07 | 0.07 | 0.06 | 0.6 |
材积量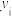 | 0.25 | 0.40 | 0.22 | 0.54 | 0.51 | 0.34 | 0.36 | 0.46 | 0.42 | 0.40 | 3.9 |
 .
.(1)估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量;
(2)求该林区这种树木的根部横截面积与材积量的样本相关系数(精确到0.01);
(3)现测量了该林区所有这种树木的根部横截面积,并得到所有这种树木的根部横截面积总和为
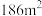 .已知树木的材积量与其根部横截面积近似成正比.利用以上数据给出该林区这种树木的总材积量的估计值.
.已知树木的材积量与其根部横截面积近似成正比.利用以上数据给出该林区这种树木的总材积量的估计值.附:相关系数
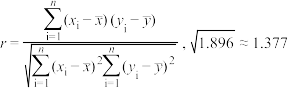 .
.
您最近一年使用:0次
2022-06-07更新
|
48116次组卷
|
63卷引用:辽宁新高考联盟(点石联考)2023-2024学年高二下学期3月联合考试数学试题
辽宁新高考联盟(点石联考)2023-2024学年高二下学期3月联合考试数学试题2022年高考全国乙卷数学(理)真题2022年高考全国乙卷数学(文)真题(已下线)2022年全国高考乙卷数学(理)试题变式题9-12题(已下线)2022年全国高考乙卷数学(文)试题变式题9-12题(已下线)第8讲 计数原理与概率统计(2021-2022年高考真题)甘肃省庆阳市宁县2021-2022学年高二下学期期末考试数学(理)试题甘肃省庆阳市宁县2021-2022学年高二下学期期末考试数学(文)试题河南省郑州市第四高级中学2023届高三第一次调研考试数学(理科)试题(已下线)专题13 概率统计解答题(已下线)专题14 概率统计解答题-1陕西省西安市雁塔区第二中学、渭北中学2021-2022学年高二下学期期末联考理科数学试题陕西省安康中学2022-2023学年高三上学期第一次检测性考试理科数学试题(已下线)第03讲 成对数据的统计分析 (精讲)(已下线)第09讲 高考中的概率与统计 (精讲)-2(已下线)2022年全国高考乙卷数学(理)试题变式题17-20题(已下线)2022年全国高考乙卷数学(文)试题变式题17-20题(已下线)考向43 统计与统计案例(九大经典题型)-4(已下线)考向38统计与统计案例(重点)-1(已下线)考向43 统计与统计案例(九大经典题型)-1(已下线)第01讲 统计(练)(已下线)专题1 2022高考命题分析与专家整体解读(已下线)专题9 2022年高考“概率与统计”专题命题分析(已下线)专题10 概率与统计的综合运用(精讲精练)-1(已下线)专题3 “数学建模”类型广东省惠州市2023届高三第三次调研数学试题(已下线)专题11-1 直方图、回归方程(线性与非线性)-2(已下线)专题7 第2讲 统计、统计案例四川省成都市玉林中学2023届高三二诊模拟理科数学试题(一)(已下线)第八章 成对数据的统计分析 (单元测)(已下线)模块三 专题6 概率与统计福建省三明第一中学2022-2023学年高二下学期期中考试数学试题(已下线)重组卷03(已下线)重组卷02(理科)(已下线)专题15 押全国卷第19题 统计与概率(已下线)专题9-2 概率与统计归类(讲+练)(已下线)专题25 统计类(解答题)+概率(几何概型)-3(已下线)第12讲 变量间的相关关系6种题型总结(2)江苏省镇江中学2023届高三下学期3月大练1数学试题全国甲乙卷真题5年分类汇编《概率统计》解答题全国甲乙卷3年真题分类汇编《概率统计》解答题(已下线)拓展一:近八年统计案例高考真题分类汇编 -【帮课堂】2022-2023学年高二数学同步精品讲义(人教A版2019选择性必修第三册)(已下线)专题09 计数原理与概率统计-1河南省南阳市唐河县唐河县第一高级中学2022-2023学年高二下学期3月月考数学试题河南省洛阳市汝阳县第一高级中学2023-2024学年高三上学期第一次月考数学试题北师大版(2019) 选修第一册 章末检测卷(六) 统计案例新疆乌鲁木齐市第六十一中学2024届高三上学期第一次月考数学(文)试题(已下线)第三节 成对数据的统计分析(第一课时) A卷素养养成卷 一轮复习点点通(已下线)第三节 成对数据的统计分析(第一课时)(核心考点集训)一轮复习点点通(已下线)考点18 决策的选择问题 2024届高考数学考点总动员(已下线)考点15 成对数据的统计相关性 2024届高考数学考点总动员(已下线)第七章 统计案例(单元基础检测卷)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)专题16回归分析(已下线)第3讲:决策的选择问题【练】(已下线)第5讲:成对数据的统计分析(非线性回归)【练】(已下线)专题08 统计案例分析(讲义)(已下线)专题11 统计与概率(分层练)(已下线)【一题多变】 相关关系 回归分析(已下线)专题10.1 概率与统计的综合运用【十一大题型】(举一反三)(新高考专用)-2江西省南昌市第二中学等部分学校2024届高三下学期3月联考数学试题(已下线)8.2.1一元线性回归模型+8.2.2一元线性回归模型 第三课 知识扩展延伸(已下线)专题25 概率统计解答题(文科)(已下线)专题25 概率统计解答题(理科)-3
名校
解题方法
3 . 马尔科夫链是概率统计中的一个重要模型,也是机器学习和人工智能的基石,在强化学习、自然语言处理、金融领域、天气预测等方面都有着极其广泛的应用.其数学定义为:假设我们的序列状态是…,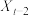 ,
,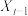 ,
,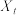 ,
, ,…,那么
,…,那么 时刻的状态的条件概率仅依赖前一状态
时刻的状态的条件概率仅依赖前一状态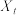 ,即
,即 .
.
现实生活中也存在着许多马尔科夫链,例如著名的赌徒模型.
假如一名赌徒进入赌场参与一个赌博游戏,每一局赌徒赌赢的概率为 ,且每局赌赢可以赢得1元,每一局赌徒赌输的概率为
,且每局赌赢可以赢得1元,每一局赌徒赌输的概率为 ,且赌输就要输掉1元.赌徒会一直玩下去,直到遇到如下两种情况才会结束赌博游戏:一种是手中赌金为0元,即赌徒输光;一种是赌金达到预期的B元,赌徒停止赌博.记赌徒的本金为
,且赌输就要输掉1元.赌徒会一直玩下去,直到遇到如下两种情况才会结束赌博游戏:一种是手中赌金为0元,即赌徒输光;一种是赌金达到预期的B元,赌徒停止赌博.记赌徒的本金为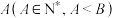 ,赌博过程如下图的数轴所示.
,赌博过程如下图的数轴所示. ,
, )时,
)时,最终输光的概率为 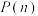 ,请回答下列问题:
,请回答下列问题:
(1)请直接写出 与
与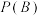 的数值.
的数值.
(2)证明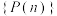 是一个等差数列,并写出公差d.
是一个等差数列,并写出公差d.
(3)当 时,分别计算
时,分别计算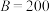 ,
, 时,
时,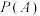 的数值,并结合实际,解释当
的数值,并结合实际,解释当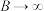 时,
时,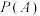 的统计含义.
的统计含义.
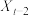 ,
,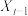 ,
,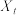 ,
, ,…,那么
,…,那么 时刻的状态的条件概率仅依赖前一状态
时刻的状态的条件概率仅依赖前一状态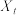 ,即
,即 .
.现实生活中也存在着许多马尔科夫链,例如著名的赌徒模型.
假如一名赌徒进入赌场参与一个赌博游戏,每一局赌徒赌赢的概率为
 ,且每局赌赢可以赢得1元,每一局赌徒赌输的概率为
,且每局赌赢可以赢得1元,每一局赌徒赌输的概率为 ,且赌输就要输掉1元.赌徒会一直玩下去,直到遇到如下两种情况才会结束赌博游戏:一种是手中赌金为0元,即赌徒输光;一种是赌金达到预期的B元,赌徒停止赌博.记赌徒的本金为
,且赌输就要输掉1元.赌徒会一直玩下去,直到遇到如下两种情况才会结束赌博游戏:一种是手中赌金为0元,即赌徒输光;一种是赌金达到预期的B元,赌徒停止赌博.记赌徒的本金为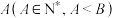 ,赌博过程如下图的数轴所示.
,赌博过程如下图的数轴所示.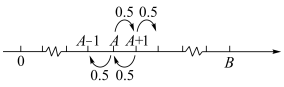
 ,
, )时,
)时,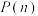 ,请回答下列问题:
,请回答下列问题:(1)请直接写出
 与
与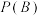 的数值.
的数值.(2)证明
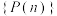 是一个等差数列,并写出公差d.
是一个等差数列,并写出公差d.(3)当
 时,分别计算
时,分别计算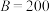 ,
, 时,
时,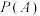 的数值,并结合实际,解释当
的数值,并结合实际,解释当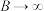 时,
时,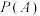 的统计含义.
的统计含义.
您最近一年使用:0次
2023-04-06更新
|
10488次组卷
|
20卷引用:辽宁省沈阳市第二中学2024届高三下学期开学考试数学试题
辽宁省沈阳市第二中学2024届高三下学期开学考试数学试题浙江省杭州市2023届高三下学期教学质量检测(二模)数学试题(已下线)专题10 计数原理与概率统计(理科)(已下线)模块二 专题4 条件概率与全概率公式(已下线)专题08 概率统计及计数原理(已下线)押新高考第19题 概率统计江西省景德镇一中2022-2023学年高二(19班)下学期期中考试数学试题湖南师范大学附属中学2023届高三三模数学试题(已下线)第四篇 概率与统计 专题6 随机游走与马尔科夫过程 微点1 随机游走与马尔科夫链广东省佛山市南海区第一中学2024届高三上学期10月月考数学试题(已下线)重难点突破01 概率与统计的综合应用(十八大题型)-3(已下线)概 率专题14条件概率与全概率公式(已下线)专题03 条件概率与全概率公式(2)(已下线)专题04 概率统计大题(已下线)专题8-2分布列综合归类-2(已下线)湖南省郴州市2024届高三一模数学试题变式题17-22(已下线)专题6 全概率与数列结合问题河南省信阳市新县高级中学2024届高三下学期适应性考试(八)数学试题单元测试B卷——第七章 随机变量及其分布
真题
名校
4 . 甲、乙、丙三位同学进行羽毛球比赛,约定赛制如下:累计负两场者被淘汰;比赛前抽签决定首先比赛的两人,另一人轮空;每场比赛的胜者与轮空者进行下一场比赛,负者下一场轮空,直至有一人被淘汰;当一人被淘汰后,剩余的两人继续比赛,直至其中一人被淘汰,另一人最终获胜,比赛结束.经抽签,甲、乙首先比赛,丙轮空.设每场比赛双方获胜的概率都为 ,
,
(1)求甲连胜四场的概率;
(2)求需要进行第五场比赛的概率;
(3)求丙最终获胜的概率.
 ,
,(1)求甲连胜四场的概率;
(2)求需要进行第五场比赛的概率;
(3)求丙最终获胜的概率.
您最近一年使用:0次
2020-07-08更新
|
42698次组卷
|
103卷引用:辽宁省大连市2023-2024学年高一上学期末模拟考试数学试题
辽宁省大连市2023-2024学年高一上学期末模拟考试数学试题辽宁省沈阳市新民市第一高级中学2023-2024学年高二下学期期初考试数学试题辽宁省沈阳市翔宇中学2023-2024学年高二下学期第一次月考测试数学试题2020年全国统一高考数学试卷(理科)(新课标Ⅰ)专题08+概率与统计-2021高考数学(理)高频考点、热点题型归类强化(已下线)易错点11 概率统计-备战2021年新高考数学一轮复习易错题(已下线)专题15 概率与统计(解答题)——三年(2018-2020)高考真题理科数学分项汇编(已下线)专题16 概率与统计综合-五年(2016-2020)高考数学(理)真题分项(已下线)第七单元概率与统计(A卷 基础过关检查)-2021年高考数学一轮复习单元滚动双测卷(新高考地区专用)(已下线)专题09 概率与统计——2020年高考真题和模拟题理科数学分项汇编(已下线)专题32 概率和统计【理】-十年(2011-2020)高考真题数学分项(四)(已下线)考点33 离散型随机变量的概率-2021年高考数学三年真题与两年模拟考点分类解读(新高考地区专用)(已下线)专题19 概率与统计综合-2020年高考数学(理)母题题源解密(全国Ⅰ专版)(已下线)重难点4 概率与统计-2021年高考数学【热点·重点·难点】专练(山东专用)(已下线)专题11.7 二项分布、正态分布(练)-2021年新高考数学一轮复习讲练测(已下线)热点11 概率与统计-2021年高考数学【热点·重点·难点】专练(新高考)(已下线)考点51 概率的性质和事件的相互独立性、条件概率-备战2021年新高考数学一轮复习考点一遍过(已下线)考点50 随机事件的概率-备战2021年高考数学(理)一轮复习考点一遍过(已下线)模块检测卷二(A卷 基础过关检查)-2021年高考数学一轮复习单元滚动双测卷(新高考地区专用)(已下线)第四章复习与小结A基础练安徽省六安市城南中学2020-2021学年高三上学期第二次月考数学(理)试题(已下线)重组卷05-冲刺2021年高考数学(理)之精选真题+模拟重组卷(新课标卷)(已下线)精做03 概率与统计-备战2021年高考数学(理)大题精做(已下线)精做03 概率与统计-备战2021年高考数学大题精做(新高考专用)(已下线)专题4.3 统计与概率-2021年高考数学解答题挑战满分专项训练(新高考地区专用)(已下线)重组卷05-冲刺2021年高考数学之精选真题+模拟重组卷(新高考地区专用)(已下线)专题23 概率与统计相结合问题(练)-2021年高三数学二轮复习讲练测(新高考版)(已下线)解密09 概率、随机变量及其分布列(讲义)-【高频考点解密】2021年新高考数学二轮复习讲义+分层训练(已下线)专题12 概率-备战2021年高考数学(理)纠错笔记(已下线)专题27 概率与统计相结合问题(练)-2021年高三数学二轮复习讲练测(文理通用)(已下线)理科数学-2021年高考考前20天终极冲刺攻略(四)(课标全国卷)(5月30日)山西省运城市新康国际实验学校2021届高三下学期5月测试数学(理)试题(已下线)数学-2021年高考考前20天终极冲刺攻略(三)(新高考地区专用)【学科网名师堂】(6月3日)(已下线)专题15 随机变量的分布列与期望 -备战2021年新高考数学纠错笔记 山东省济宁市兖州区2020-2021学年高二下学期期中考试数学试题湖南省衡阳市第八中学2020-2021学年高一下学期期末数学试题(已下线)解密21 统计与概率(分层训练)-【高频考点解密】2021年高考数学(理)二轮复习讲义+分层训练(已下线)预测12 概率统计-【临门一脚】2021年高考数学三轮冲刺过关(新高考专用)【学科网名师堂】(已下线)押第19题 概率统计-备战2021年高考数学(理)临考题号押题(全国卷1)湖南省邵阳市邵阳县2020-2021学年高一下学期期末数学试题(已下线)考点42 随机事件及其概率-备战2022年高考数学一轮复习考点帮(浙江专用)(已下线)考点43 古典概型-备战2022年高考数学一轮复习考点帮(浙江专用)(已下线)考点40 离散型随机变量的分布列、均值与方差-备战2022年高考数学(理)一轮复习考点微专题(已下线)专题14 概率统计-十年(2012-2021)高考数学真题分项汇编(全国通用)人教B版(2019) 选修第二册 过关检测 第四章 专项把关练北师大版(2019) 必修第一册 突围者 第七章 章末培优专练(已下线)专题11.7 二项分布、正态分布 2022年高考数学一轮复习讲练测(新教材新高考)(练)(已下线)专题09 计数原理与概率与统计(理)-五年(2017-2021)高考数学真题分项汇编(文科+理科)(已下线)专题17 概率统计(解答题)-备战2022年高考数学(理)母题题源解密(全国甲卷)(已下线)2020年高考全国1数学理高考真题变式题16-20题(已下线)技巧04 解答题解法与技巧(讲)--第二篇 解题技巧篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》(已下线)专题20统计概率(理科)解答题20题-备战2022年高考数学冲刺横向强化精练精讲江苏省南京市金陵中学2022届高三下学期3月学情调研数学试题(已下线)第七章 随机变量及其分布(选拔卷)-【单元测试】2021-2022学年高二数学尖子生选拔卷(人教A版2019选择性必修第三册)(已下线)专题50 盘点古典(几何概型)概型及条件概率问题——备战2022年高考数学二轮复习常考点专题突破福建省永春第一中学2021-2022学年高二3月线上考试数学试题人教A版(2019) 选修第三册 一蹴而就 第七章 单元整合人教A版(2019) 选修第三册 实战演练 第七章验收检测(已下线)专题1 概率、二项分布与正态分布-学会解题之高三数学321训练体系【2022版】沪教版(2020) 必修第三册 达标检测 期末测试(已下线)解密17 概率统计(分层训练)-【高频考点解密】2022年高考数学二轮复习讲义+分层训练(浙江专用)(已下线)回归教材重难点06 概率与统计-【查漏补缺】2022年高考数学(理)三轮冲刺过关(已下线)押全国卷(理科)第18题 概率与统计-备战2022年高考数学(理)临考题号押题(全国卷)(已下线)2022年高考考前20天终极冲刺攻略(三)【数学】(新高考地区专用)(6月2日)(已下线)2022年高考考前20天终极冲刺攻略(四)【理科数学】(6月3日)(已下线)第03讲 互斥事件和独立事件-【帮课堂】2021-2022学年高一数学同步精品讲义(苏教版2019必修第二册)河北省邯郸市大名县第一中学2021-2022学年高二下学期6月月考数学试题上海市七宝中学2021-2022学年高二下学期期末数学试题陕西省渭南市富平县2021-2022学年高二下学期期末文科数学试题(已下线)专题13 概率统计解答题苏教版(2019) 必修第二册 必杀技 第15章 概率 素养检测(已下线)考点26 概率、二项分布与正态分布-1-(核心考点讲与练)-2023年高考数学一轮复习核心考点讲与练(新高考专用)苏教版(2019) 必修第二册 过关斩将 第15章 15.1~15.3 综合拔高练2023版 北师大版(2019) 必修第一册 突围者 第七章 章末培优专练2023版 湘教版(2019) 选修第二册 过关斩将 第3章 综合拔高练广东省佛山市顺德区华侨中学2022-2023学年高二上学期10月月考数学试题(已下线)考向40 事件的相互独立性、条件概率与全概率公式(七大经典题型)-2山东省济宁市育才中学2022-2023学年高二上学期第一次学情检测数学试题(已下线)考向44事件的独立性与条件概率(重点)-3河南省南阳市南召现代中学2022-2023学年高一上学期11月考试数学试题沪教版(2020) 一轮复习 堂堂清 第九单元 9.4 随机事件的概率(已下线)专题11-2 概率与分布列大题归类-2陕西省西安交通大学附属中学2019-2020学年高二下学期7月月考理科数学试题第七章 概率单元练习——2022-2023学年高一上学期数学北师大版(2019)必修第一册(已下线)重组卷04(已下线)专题26 概率综合问题(分布列)(解答题)(理科)-2第15章 概率(单元测试)(已下线)专题14 概率-期中期末考点大串讲(苏教版2019必修第二册)2023版 湘教版(2019) 必修第二册 过关斩将 第5章 综合拔高练全国甲乙卷真题5年分类汇编《概率统计》解答题(已下线)上海高二下学期期末真题精选(常考60题41个考点专练)-【满分全攻略】2022-2023学年高二数学下学期核心考点+重难点讲练与测试(沪教版2020选修一+选修二)(已下线)核心考点11 概率初步(续)-【满分全攻略】2022-2023学年高二数学下学期核心考点+重难点讲练与测试(沪教版2020选修一+选修二)(已下线)第四篇 概率与统计 专题4 分赌注问题 微点1 分赌注问题北师大版(2019) 必修第一册 数学奇书 学业评价(四十八)事件的独立性(已下线)第四篇 概率与统计 专题6 随机游走与马尔科夫过程 微点1 随机游走与马尔科夫链(已下线)第四篇 概率与统计 专题7 常见分布 微点2 其它分布四川省兴文第二中学校2023-2024学年高二上学期10月月考数学试题(已下线)第06讲 事件的相互独立性、条件概率与全概率公式(练习)1号卷·A10联盟2022届全国高考第一轮总复习试卷数学(理科)试题(十九)(已下线)【一题多变】 比赛概率 三思五步(已下线)8.5 二项分布、超几何分布与正态分布(高考真题素材之十年高考)(已下线)专题25 概率统计解答题(理科)-1(已下线)专题02 事件的相互独立性(题型专练)-《知识解读·题型专练》(人教A版2019必修第二册)
5 . 某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:

(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数 ,并将完成生产任务所需时间超过
,并将完成生产任务所需时间超过 和不超过
和不超过 的工人数填入下面的列联表:
的工人数填入下面的列联表:
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附: ,
,

(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数
 ,并将完成生产任务所需时间超过
,并将完成生产任务所需时间超过 和不超过
和不超过 的工人数填入下面的列联表:
的工人数填入下面的列联表:超过 | 不超过 | |
| 第一种生产方式 | ||
| 第二种生产方式 |
附:
 ,
, 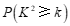 | 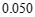 | 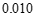 |  |
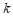 | 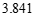 | 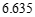 |  |
您最近一年使用:0次
2018-06-09更新
|
39906次组卷
|
89卷引用:辽宁省沈阳市五校协作体2019-2020学年高三上学期期中考试数学(文)试题
辽宁省沈阳市五校协作体2019-2020学年高三上学期期中考试数学(文)试题2018年全国普通高等学校招生统一考试文科数学(新课标III卷)2018年全国普通高等学校招生统一考试理科数学(新课标III卷)(已下线)2018年高考题及模拟题汇编 【理科】7.概率与统计(已下线)2018年高考题及模拟题汇编 【文科】7.概率与统计【全国百强校】山东省济南市历城第二中学2017-2018学年高二下学期阶段考试(6月月考)数学(文)试题【全国百强校】山东省济南外国语学校2017-2018学年高二下学期期末教学质量检测数学(文)试题河北省临漳县第一中学2017-2018学年高二下学期第三次月考数学(文)试题【校级联考】四川省眉山一中办学共同体2019届高三10月月考数学(文)试卷【市级联考】甘肃省酒泉地区普通高中五校联考2019届高三上学期月考数学试题(已下线)2018年11月19日 《每日一题》理数人教版一轮复习-独立性检验 (已下线)2018年11月29日 《每日一题》【文科】一轮复习-独立性检验【校级联考】江西省上饶市“山江湖”协作体2018-2019学年高二上学期第三次月考数学(文)试题(已下线)2019年3月5日 《每日一题》(理)二轮复习-独立性检验(已下线)2019年3月13日 《每日一题》文科二轮复习 独立性检验【全国百强校】安徽省铜陵市第一中学2018-2019学年高二下学期期中考试数学(文)试题(已下线)2019年5月26日 《每日一题》理数选修2-3-每周一测四川省树德中学2018-2019学年高二5月阶段性测试数学(文)试题吉林省吉林市三校2018-2019学年度高二下学期期末数学(理)试卷(已下线)2019年11月18日《每日一题》一轮复习理数-独立性检验(已下线)2019年11月28日《每日一题》一轮复习文数-独立性检验(已下线)7.概率与统计[文] -《备战2020年高考精选考点专项突破题集》(已下线)专题10.3 变量间的相关关系与统计案例(讲)【理】-《2020年高考一轮复习讲练测》(已下线)专题10.3 变量间的相关关系与统计案例(讲)【文】-《2020年高考一轮复习讲练测》专题07 概率与统计[理]-《备战2020年高考精选考点专项突破题集》2020届福建省福州市第一中学高三第四次调研数学理科试题专题10.2 统计与统计案例(练)-江苏版《2020年高考一轮复习讲练测》黑龙江省牡丹江市第一高级中学2018-2019学年高二寒假开学检测数学(文)试题湖北省华中师范大学第一附属中学2019-2020学年高二下学期期中数学试题(已下线)专题03 独立性检验(第四篇)-备战2020年高考数学大题精做之解答题题型全覆盖广西天等中学2019-2020学年高二上学期期中考试数学文科试题河南省郑州市中牟县第一高级中学2019-2020学年下学期高二期中考试数学试题广西柳城县中学2020届高三6月加强考数学(文科)试题(已下线)专题18 统计综合-2020年高考数学(文)母题题源解密(全国Ⅲ专版)(已下线)专题15 概率与统计(解答题)——三年(2018-2020)高考真题文科数学分项汇编(已下线)专题16 概率与统计综合-五年(2016-2020)高考数学(文)真题分项(已下线)综合测试卷(巅峰版)突破满分数学之2019-2020学年高二数学(理)重难点突破(人教A版选修2-3)(已下线)突破3.2独立性检验的基本思想及其初步应用-突破满分数学之2019-2020学年高二数学(理)课时训练(人教A版选修2-3)(已下线)突破3.2独立性检验的基本思想及其初步应用-突破满分数学之2019-2020学年高二数学(理)重难点突破(人教A版选修2-3)(已下线)专题15 概率与统计(解答题)——三年(2018-2020)高考真题理科数学分项汇编(已下线)专题16 概率与统计综合-五年(2016-2020)高考数学(理)真题分项(已下线)专题18 统计综合-2020年高考数学(理)母题题源解密(全国Ⅲ专版)广东省佛山市禅城区2019-2020学年高二下学期期末数学试题(已下线)专题31 概率和统计【文】-十年(2011-2020)高考真题数学分项(已下线)专题32 概率和统计【理】-十年(2011-2020)高考真题数学分项(六)(已下线)考点34 变量的相关关系与统计案例-2021年高考数学三年真题与两年模拟考点分类解读(新高考地区专用)(已下线)考点44 独立性检验-备战2021年高考数学(文)一轮复习考点一遍过(已下线)考点46 独立性检验-备战2021年高考数学(理)一轮复习考点一遍过山西省大同市煤矿第四中学校2021届高三上学期期中数学(文)试题(已下线)专题10.3 变量相关性与统计案例 (精讲) -2021年高考数学(理)一轮复习讲练测(已下线)专题10.2 变量相关性与统计案例(精讲)-2021年高考数学(文)一轮复习学与练(已下线)专题10.2 变量相关性与统计案例(精讲)-2021年高考数学(理)一轮复习学与练山东省济南第一中学2021届高三上学期期中数学试题西藏自治区林芝市第二高级中学2021届高三上学期第三次月考数学(理)试题(已下线)专题4.3 统计与概率-2021年高考数学解答题挑战满分专项训练(新高考地区专用)(已下线)押第3题 统计图表-备战2021年高考数学(文)临考题号押题(全国卷1)(已下线)押第3题 统计图表-备战2021年高考数学(理)临考题号押题(全国卷1)(已下线)专题23 概率与统计相结合问题(练)-2021年高三数学二轮复习讲练测(新高考版)(已下线)专题27 概率与统计相结合问题(练)-2021年高三数学二轮复习讲练测(文理通用)(已下线)文科数学-2021年高考考前20天终极冲刺攻略+(三)(6月2日)(已下线)第三章 统计案例【专项训练】-2020-2021学年高二数学(理)下学期期末专项复习(人教A版选修2-3)(已下线)解密21 统计与概率(分层训练)-【高频考点解密】2021年高考数学(理)二轮复习讲义+分层训练宁夏石嘴山市第一中学2020—2021学年高二下学期期中数学(理)考试题广东省深圳市人大附中学深圳学校2020-2021学年高二下学期期中数学试题宁夏银川一中2022届高三上学期第一次月考数学(理)试题福建省南平市浦城县2018-2019学年高二下学期第一次月考数学(文)试题(已下线)专题14 概率统计-十年(2012-2021)高考数学真题分项汇编(全国通用)(已下线)专题09 概率与统计(文)-五年(2017-2021)高考数学真题分项汇编(文科+理科)(已下线)专题09 计数原理与概率与统计(理)-五年(2017-2021)高考数学真题分项汇编(文科+理科)四川省宜宾市第四中学2022届高三二诊模拟考试数学(文)试题内蒙古包头市第四中学2020-2021学年高三上学期期中考试数学(理)试题(已下线)专题51 盘点统计初步及独立性检验问题——备战2022年高考数学二轮复习常考点专题突破广西河池市八校2021-2022学年高二下学期第一次联考数学(文)试题(已下线)2022年高考考前最后一课-数学(正式版)-【考前预测篇2】命题专家押题陕西省宝鸡市渭滨区2021-2022学年高二下学期期末理科数学试题陕西省宝鸡市渭滨区2021-2022学年高二下学期期末文科数学试题(已下线)专题13 概率统计解答题(已下线)专题14 概率统计解答题-2四川省遂宁市射洪中学2022-2023学年高三上学期入学考试数学理试题四川省南充高级中学2022-2023学年高三上学期第4次模拟测试数学理科试题四川省南充高级中学2022-2023学年高三上学期第四次月考数学试题(理)重庆市永川北山中学校2022届高三高考冲刺5数学试题广西玉林市第十一中学2021-2022学年高二下学期3月月考数学试题(文科)四川省泸县第五中学2022-2023学年高三下学期开学考试数学(理)试题(已下线)拓展一:近八年统计案例高考真题分类汇编 -【帮课堂】2022-2023学年高二数学同步精品讲义(人教A版2019选择性必修第三册)专题17列联表与独立性检验(已下线)9.2 成对数据的分析(高考真题素材之十年高考)(已下线)专题25 概率统计解答题(文科)(已下线)专题25 概率统计解答题(理科)-3
名校
6 . 2023年,全国政协十四届一次会议于3月4日下午3时在人民大会堂开幕,3月11日下午闭幕,会期7天半;十四届全国人大一次会议于3月5日上午开幕,13日上午闭幕,会期8天半.为调查学生对两会相关知识的了解情况,某高中学校开展了两会知识问答活动,现从全校参与该活动的学生中随机抽取320名学生,他们的得分(满分100分)的频率分布折线图如下.
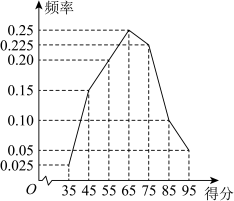
(1)若此次知识问答的得分 ,用样本来估计总体,设
,用样本来估计总体,设 ,
, 分别为被抽取的320名学生得分的平均数和标准差,求
分别为被抽取的320名学生得分的平均数和标准差,求 的值;
的值;
(2)学校对这些被抽取的320名学生进行奖励,奖励方案如下:用频率估计概率,得分小于或等于55的学生获得1次抽奖机会,得分高于55的学生获得2次抽奖机会.假定每次抽奖抽到价值10元的学习用品的概率为 ,抽到价值20元的学习用品的概率为
,抽到价值20元的学习用品的概率为 .从这320名学生中任取一位,记该同学在抽奖活动中获得学习用品的价值总额为
.从这320名学生中任取一位,记该同学在抽奖活动中获得学习用品的价值总额为 元,求
元,求 的分布列和数学期望(用分数表示),并估算此次抽奖要准备的学习用品的价值总额.
的分布列和数学期望(用分数表示),并估算此次抽奖要准备的学习用品的价值总额.
参考数据: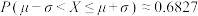 ,
,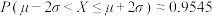 ,
,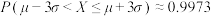 ,
,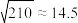 ,
,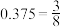 .
.

(1)若此次知识问答的得分
 ,用样本来估计总体,设
,用样本来估计总体,设 ,
, 分别为被抽取的320名学生得分的平均数和标准差,求
分别为被抽取的320名学生得分的平均数和标准差,求 的值;
的值;(2)学校对这些被抽取的320名学生进行奖励,奖励方案如下:用频率估计概率,得分小于或等于55的学生获得1次抽奖机会,得分高于55的学生获得2次抽奖机会.假定每次抽奖抽到价值10元的学习用品的概率为
 ,抽到价值20元的学习用品的概率为
,抽到价值20元的学习用品的概率为 .从这320名学生中任取一位,记该同学在抽奖活动中获得学习用品的价值总额为
.从这320名学生中任取一位,记该同学在抽奖活动中获得学习用品的价值总额为 元,求
元,求 的分布列和数学期望(用分数表示),并估算此次抽奖要准备的学习用品的价值总额.
的分布列和数学期望(用分数表示),并估算此次抽奖要准备的学习用品的价值总额.参考数据:
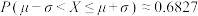 ,
,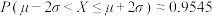 ,
,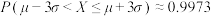 ,
,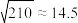 ,
,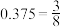 .
.
您最近一年使用:0次
2023-04-09更新
|
3546次组卷
|
11卷引用:辽宁省县级重点高中联合体2023届高三二模数学试题
辽宁省县级重点高中联合体2023届高三二模数学试题山西省部分学校2023届高三下学期4月联考数学试题河南省创新发展联盟2023届高三下学期二模考试数学(理)试题陕西省商洛市2023届高三二模理科数学试题吉林省白山市2023届高三下学期四模联考(4月期中)数学试题(已下线)数学(新高考Ⅱ卷)(已下线)押新高考第19题 概率统计(已下线)模块六 专题4 易错题目重组卷(辽宁卷)(已下线)第8章 概率 单元测试(B卷重难过关)-【学霸满分】2022-2023学年高二数学下学期重难点专题提优训练(苏教版2019选择性必修第二册)(已下线)拓展二:离散型随机变量的分布列与数字特征11种常见考法归类(2)宁夏回族自治区石嘴山市大武口区石嘴山市第三中学2023届高三三模理科数学试题
名校
7 . 在统计学的实际应用中,除了中位数外,经常使用的是25%分位数(简称为第一四分位数)与75%分位数(简称为第三四分位数),四分位数应用于统计学的箱型图绘制,是统计学中分位数的一种,即把所有数值由小到大排列,并分成四等份,处于三个分割点的数值就是四分位数,箱型图中“箱体”的下底边对应数据为第一四分位数,上底边对应数据为第三四分位数,中间的线对应中位数,已知甲、乙两班人数相同,在一次测试中两班成绩箱型图如图所示.
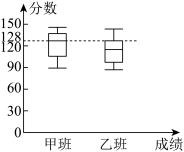
(1)由此图估计甲、乙两班平均分较高的班级是哪个?(直接给出结论即可,不用说明理由)
(2)若在两班中随机抽取一人,发现他的分数小于128分,则求该同学来自甲班和乙班的概率分别是多少?
(3)据统计两班中高于140分共10人,其中甲班6人,乙班4人,从中抽取了3人作学习经验交流,3人中来自乙班的人数为 ,求
,求 的分布列.
的分布列.

(1)由此图估计甲、乙两班平均分较高的班级是哪个?(直接给出结论即可,不用说明理由)
(2)若在两班中随机抽取一人,发现他的分数小于128分,则求该同学来自甲班和乙班的概率分别是多少?
(3)据统计两班中高于140分共10人,其中甲班6人,乙班4人,从中抽取了3人作学习经验交流,3人中来自乙班的人数为
 ,求
,求 的分布列.
的分布列.
您最近一年使用:0次
2024-03-01更新
|
2854次组卷
|
4卷引用:东北三省三校(哈师大附中、东北师大附中、辽宁省实验中学)2023-2024学年高三下学期第一次联合模拟考数学试题
东北三省三校(哈师大附中、东北师大附中、辽宁省实验中学)2023-2024学年高三下学期第一次联合模拟考数学试题湖南省2024届高三数学新改革提高训练五(九省联考题型)(已下线)7.2离散型随机变量及其分布列 第三课 知识扩展延伸(已下线)7.2 离散型随机变量及其分布列——课后作业(巩固版)
名校
解题方法
8 . 为弘扬中国共产党百年奋斗的光辉历程,某校团委决定举办“中国共产党党史知识”竞赛活动.竞赛共有 和
和 两类试题,每类试题各10题,其中每答对1道
两类试题,每类试题各10题,其中每答对1道 类试题得10分;每答对1道
类试题得10分;每答对1道 类试题得20分,答错都不得分.每位参加竞赛的同学从这两类试题中共抽出3道题回答(每道题抽后不放回).已知某同学
类试题得20分,答错都不得分.每位参加竞赛的同学从这两类试题中共抽出3道题回答(每道题抽后不放回).已知某同学 类试题中有7道题能答对,而他答对各道
类试题中有7道题能答对,而他答对各道 类试题的概率均为
类试题的概率均为 .
.
(1)若该同学只抽取3道 类试题作答,设
类试题作答,设 表示该同学答这3道试题的总得分,求
表示该同学答这3道试题的总得分,求 的分布和期望;
的分布和期望;
(2)若该同学在 类试题中只抽1道题作答,求他在这次竞赛中仅答对1道题的概率.
类试题中只抽1道题作答,求他在这次竞赛中仅答对1道题的概率.
 和
和 两类试题,每类试题各10题,其中每答对1道
两类试题,每类试题各10题,其中每答对1道 类试题得10分;每答对1道
类试题得10分;每答对1道 类试题得20分,答错都不得分.每位参加竞赛的同学从这两类试题中共抽出3道题回答(每道题抽后不放回).已知某同学
类试题得20分,答错都不得分.每位参加竞赛的同学从这两类试题中共抽出3道题回答(每道题抽后不放回).已知某同学 类试题中有7道题能答对,而他答对各道
类试题中有7道题能答对,而他答对各道 类试题的概率均为
类试题的概率均为 .
.(1)若该同学只抽取3道
 类试题作答,设
类试题作答,设 表示该同学答这3道试题的总得分,求
表示该同学答这3道试题的总得分,求 的分布和期望;
的分布和期望;(2)若该同学在
 类试题中只抽1道题作答,求他在这次竞赛中仅答对1道题的概率.
类试题中只抽1道题作答,求他在这次竞赛中仅答对1道题的概率.
您最近一年使用:0次
2023-11-24更新
|
2910次组卷
|
9卷引用:辽宁省大连市第八中学2023-2024学年高二下学期4月月考数学试题
辽宁省大连市第八中学2023-2024学年高二下学期4月月考数学试题江苏省南京市六校联合体2023-2024学年高三上学期11月期中数学试题江西省宜春市宜丰县宜丰中学2024届高三上学期12月月考数学试题(已下线)江苏省南京市六校联合体2023-2024学年高三上学期11月期中数学试题变式题19-22河南省郑州市宇华实验学校2024届高三上学期12月月考数学试题(已下线)6.4.2超几何分布(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)福建省永春一中、培元中学、石光中学、季延中学2024届高三下学期第二次联合考试数学试题(已下线)黄金卷04单元测试A卷——第七章 随机变量及其分布
9 . 某项选拔共有四轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考核,否则即被淘汰.已知某选手能正确回答第一、二、三、四轮的问题的概率分别为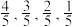 ,且各轮问题能否回答正确互不影响.
,且各轮问题能否回答正确互不影响.
(1)求该选手进入第四轮才被淘汰的概率;
(2)求该选手至多进入第三轮考核的概率.
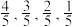 ,且各轮问题能否回答正确互不影响.
,且各轮问题能否回答正确互不影响.(1)求该选手进入第四轮才被淘汰的概率;
(2)求该选手至多进入第三轮考核的概率.
您最近一年使用:0次
2023-12-19更新
|
2756次组卷
|
17卷引用:辽宁省大连市2020-2021学年高一上学期期末数学试题
辽宁省大连市2020-2021学年高一上学期期末数学试题辽宁省营口市2022-2023学年高一上学期期末教学质量监测数学试题辽宁省营口市2022-2023学年高一下学期开学考试数学试题辽宁省沈阳市2024年普通高中学业水平合格性考试模拟数学试题(已下线)2010-2011学年广东省龙山中学高二3月月考理科数学卷(已下线)2011届四川省成都市石室中学高三三诊模拟考试文科数学2014-2015学年北京市延庆县高二下学期期末考试理科数学试卷人教B版(2019) 必修第二册 逆袭之路 第五章 5.4 统计与概率的应用 小结重庆市江津中学校2021-2022学年高二上学期开学考试数学试题(已下线)第五章 统计与概率 5.4 统计与概率的应用山东省济宁市汶上县第一中学2022-2023学年高二上学期第一次模块检测数学试题2007年普通高等学校招生考试数学(文)试题(陕西卷)人教B版(2019)必修第二册课本习题习题5-4广东省珠海市广东实验中学珠海金湾学校2023-2024学年高二上学期12月月考数学试题10.2事件的相互独立性练习(已下线)高一数学开学摸底考 01-北师大版2019必修第一册全册开学摸底考试卷单元测试A卷——第十章?概率
名校
解题方法
10 . 4月23日是联合国教科文组织确定的“世界读书日”.为了解某地区高一学生阅读时间的分配情况,从该地区随机抽取了500名高一学生进行在线调查,得到了这500名学生的日平均阅读时间(单位:小时),并将样本数据分成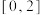 ,
, ,
, ,
, ,
,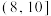 ,
,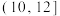 ,
,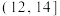 ,
,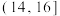 ,
,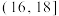 九组,绘制成如图所示的频率分布直方图.
九组,绘制成如图所示的频率分布直方图.
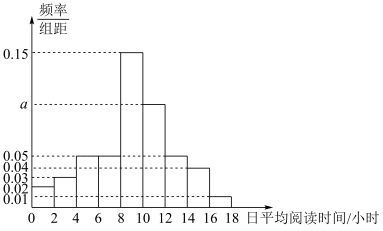
(1)从这500名学生中随机抽取一人,日平均阅读时间在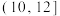 内的概率;
内的概率;
(2)为进一步了解这500名学生数字媒体阅读时间和纸质图书阅读时间的分配情况,从日平均阅读时间在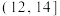 ,
,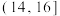 ,
,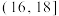 三组内的学生中,采用分层抽样的方法抽取了10人,现从这10人中随机抽取3人,记日平均阅读时间在
三组内的学生中,采用分层抽样的方法抽取了10人,现从这10人中随机抽取3人,记日平均阅读时间在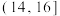 内的学生人数为X,求X的分布列和数学期望;
内的学生人数为X,求X的分布列和数学期望;
(3)以样本的频率估计概率,从该地区所有高一学生中随机抽取10名学生,用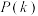 表示这10名学生中恰有k名学生日平均阅读时间在
表示这10名学生中恰有k名学生日平均阅读时间在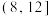 内的概率,其中
内的概率,其中 ,1,2,…,10.当
,1,2,…,10.当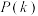 最大时,写出k的值.(只需写出结论)
最大时,写出k的值.(只需写出结论)
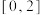 ,
, ,
, ,
, ,
,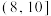 ,
,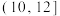 ,
,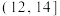 ,
,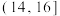 ,
,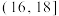 九组,绘制成如图所示的频率分布直方图.
九组,绘制成如图所示的频率分布直方图.
(1)从这500名学生中随机抽取一人,日平均阅读时间在
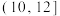 内的概率;
内的概率;(2)为进一步了解这500名学生数字媒体阅读时间和纸质图书阅读时间的分配情况,从日平均阅读时间在
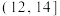 ,
,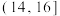 ,
,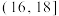 三组内的学生中,采用分层抽样的方法抽取了10人,现从这10人中随机抽取3人,记日平均阅读时间在
三组内的学生中,采用分层抽样的方法抽取了10人,现从这10人中随机抽取3人,记日平均阅读时间在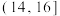 内的学生人数为X,求X的分布列和数学期望;
内的学生人数为X,求X的分布列和数学期望;(3)以样本的频率估计概率,从该地区所有高一学生中随机抽取10名学生,用
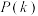 表示这10名学生中恰有k名学生日平均阅读时间在
表示这10名学生中恰有k名学生日平均阅读时间在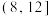 内的概率,其中
内的概率,其中 ,1,2,…,10.当
,1,2,…,10.当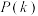 最大时,写出k的值.(只需写出结论)
最大时,写出k的值.(只需写出结论)
您最近一年使用:0次
2022-06-02更新
|
5968次组卷
|
15卷引用:辽宁省锦州市辽西育明高级中学2022-2023学年高二下学期第一次阶段性数学试题
辽宁省锦州市辽西育明高级中学2022-2023学年高二下学期第一次阶段性数学试题北京景山学校2022届高三适应性考试数学试题北京市北京理工大学附属中学2021-2022学年高二下学期限时训练15(期末模拟)试题(已下线)6.6 分布列基础(精讲)(已下线)专题14 概率、统计、期望(已下线)考向42 四大分布:两点分布、二项分布、超几何分布与正态分布(十大经典题型)-1(已下线)模块十 计数原理与统计概率-2(已下线)模块八 专题10 以概率与统计为背景的压轴大题(已下线)第四篇 概率与统计 专题2 最可能成功次数 微点1 最可能成功次数(已下线)第四篇 概率与统计 专题7 常见分布 微点3 常见分布综合训练黑龙江省鹤岗市第一中学2022-2023学年高二上学期期末数学试题(已下线)第08讲 两点分布、二项分布、超几何分布与正态分布(十一大题型)(讲义)-2专题15离散型随机变量的分布列(已下线)专题7.10 随机变量及其分布全章综合测试卷(提高篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)8.2 离散型随机变量及其分布列(3)




