1 . 本小题满分12分)根据以往的经验,某工程施工期间的降水量X(单位:mm)对工期的影响如下表:
历年气象资料表明,该工程施工期间降水量X小于300,700,900的概率分别为0.3,0.7,0.9. 求:
(Ⅰ)工期延误天数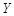 的均值与方差;
的均值与方差;
(Ⅱ)在降水量X至少是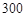 的条件下,工期延误不超过6天的概率.
的条件下,工期延误不超过6天的概率.
| 降水量X | 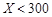 |  | 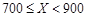 |  |
工期延误天数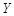 | 0 | 2 | 6 | 10 |
(Ⅰ)工期延误天数
 的均值与方差;
的均值与方差; (Ⅱ)在降水量X至少是
 的条件下,工期延误不超过6天的概率.
的条件下,工期延误不超过6天的概率.
您最近一年使用:0次
2019-01-30更新
|
2585次组卷
|
18卷引用:2012年全国普通高等学校招生统一考试理科数学(湖北卷)
2012年全国普通高等学校招生统一考试理科数学(湖北卷)(已下线)2014高考名师推荐数学理科正态分布2015届吉林省实验中学高三上学期第五次模拟考试理科数学试卷2016届河南省南阳、周口、驻马店等六市高三第一次联考理科数学试卷2015-2016新疆哈密地区二中高二下期末考试理科数学卷内蒙古包头市第一中学2016-2017学年高二下学期期中考试数学(理)试题重庆市凤鸣山中学2019-2020学年高二下学期6月月考数学试题(已下线)7.3.2 离散型随机变量的方差(练习)-2020-2021学年下学期高二数学同步精品课堂(新教材人教A版选择性必修第三册)(已下线)专题7.3离散型随机变量的数字特征(A卷基础篇)-2020-2021学年高二下学期数学选择性必修第三册同步单元AB卷(新教材人教A版,浙江专用)人教A版(2019) 选修第三册 突围者 第七章 第三节 课时2 离散型随机变量的方差黑龙江省牡丹江市第二高级中学2022-2023学年高三上学期第二次阶段测试数学试题6.3.2离散型随机变量的方差 同步练习6.3.2离散型随机变量的方差 课时作业北师大版(2019) 选修第一册 章末检测卷(五) 概率河北省秦皇岛市卢龙县第二高级中学2023-2024学年高二下学期3月月考数学试题四川省绵阳市东辰学校2024届高三下学期第二学月考试数学(理科)试题四川省成都市金堂县淮口中学校2024届高三下学高考仿真冲刺卷(一)理科数学试题【基础卷】第7章 概率初步(续)单元测试C-沪教版(2020)选择性必修第二册
2 . A、B两个投资项目的利润率分别为随机变量X1和X2.根据市场分析,X1,X2的分布列分别为
(Ⅰ)在A、B两个项目上各投资100万元,Y1和Y2分别表示投资项目A和B所获得的利润,求方差DY1,DY2;
(Ⅱ)将x(0≤x≤100)万元投资A项目,100-x万元投资B项目,f(x)表示投资A项目所得利润的方差与投资B项目所得到利润的方差的和.求f(x)的最小值,并指出x为何值时,f(x)取到最小值.
(注:D(ax+b)=a2Dx)
| X1 | 5% | 10% |
| P | 0.8 | 0.2 |
| X2 | 2% | 8% | 12% |
| P | 0.2 | 0.5 | 0.3 |
(Ⅰ)在A、B两个项目上各投资100万元,Y1和Y2分别表示投资项目A和B所获得的利润,求方差DY1,DY2;
(Ⅱ)将x(0≤x≤100)万元投资A项目,100-x万元投资B项目,f(x)表示投资A项目所得利润的方差与投资B项目所得到利润的方差的和.求f(x)的最小值,并指出x为何值时,f(x)取到最小值.
(注:D(ax+b)=a2Dx)
您最近一年使用:0次
2019-01-30更新
|
2069次组卷
|
17卷引用:2008年普通高等学校招生全国统一考试理科数学(宁夏卷)
2008年普通高等学校招生全国统一考试理科数学(宁夏卷)(已下线)2013-2014学年苏教版选修2-3高二数学双基达标2.5练习卷黑龙江省海林市朝鲜族中学人教版高中数学选修2-3同步练习:滚动习题(四)[范围2.1~2.4](已下线)高中数学新教材练习题2008年普通高等学校招生考试数学(理)试题(琼、宁卷)人教B版(2019) 选修第二册 突围者 第四章 第二节课时4 随机变量的数字特征(已下线)第五课时 课后 7.3.2 离散型随机变量的方差(已下线)第四章 概率与统计 本章小结广东省中山纪念中学等四校2021届高三下学期5月联考数学试卷(已下线)3.2.4 离散型随机变量的方差(已下线)13.3 二项分布、超几何分布与数字特征(已下线)7.3.2 离散型随机变量的方差(2)北师大版(2019) 选修第一册 数学奇书 学业评价(四十二) 离散型随机变量的方差人教B版(2019)选择性必修第二册课本习题第四章本章小结宁夏回族自治区吴忠市吴忠中学2023-2024学年高二下学期6月月考数学试卷【巩固卷】第7章 概率初步(续)单元测试B沪教版(2020)选择性必修第二册【课后练 】3.2.4 离散型随机变量的方差 课后作业-湘教版(2019)选择性必修第二册 第3章 概率
3 . 甲、乙两名射手在一次射击中得分为两个相互独立的随机变量ξ与η,且ξ,η的分布列为
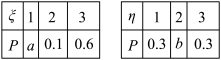
(1)求a,b的值.
(2)计算ξ,η的均值与方差,并以此分析甲、乙的技术状况.

(1)求a,b的值.
(2)计算ξ,η的均值与方差,并以此分析甲、乙的技术状况.
您最近一年使用:0次
4 . 某单位为促进职工业务技能提升,对该单位120名职工进行一次业务技能测试,测试项目共5项.现从中随机抽取了10名职工的测试结果,将它们编号后得到它们的统计结果如下表(表1)所示(“√”表示测试合格,“×”表示测试不合格).
表1:
规定:每项测试合格得5分,不合格得0分.
(1)以抽取的这10名职工合格项的项数的频率代替每名职工合格项的项数的概率.
①设抽取的这10名职工中,每名职工测试合格的项数为 ,根据上面的测试结果统计表,列出
,根据上面的测试结果统计表,列出 的分布列,并估计这120名职工的平均得分;
的分布列,并估计这120名职工的平均得分;
②假设各名职工的各项测试结果相互独立,某科室有5名职工,求这5名职工中至少有4人得分不少于20分的概率;
(2)已知在测试中,测试难度的计算公式为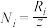 ,其中
,其中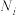 为第
为第 项测试难度,
项测试难度,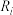 为第
为第 项合格的人数,
项合格的人数, 为参加测试的总人数.已知抽取的这10名职工每项测试合格人数及相应的实测难度如下表(表2):
为参加测试的总人数.已知抽取的这10名职工每项测试合格人数及相应的实测难度如下表(表2):
表2:
定义统计量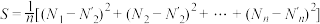 ,其中
,其中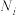 为第
为第 项的实测难度,
项的实测难度, 为第
为第 项的预测难度(
项的预测难度(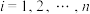 ).规定:若
).规定:若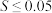 ,则称该次测试的难度预测合理,否则为不合理,测试前,预估了每个预测项目的难度,如下表(表3)所示:
,则称该次测试的难度预测合理,否则为不合理,测试前,预估了每个预测项目的难度,如下表(表3)所示:
表3:
判断本次测试的难度预估是否合理.
表1:
编号\测试项目 | 1 | 2 | 3 | 4 | 5 |
1 | × | √ | √ | √ | √ |
2 | √ | √ | √ | √ | × |
3 | √ | √ | √ | √ | × |
4 | √ | √ | √ | × | × |
5 | √ | √ | √ | √ | √ |
6 | √ | × | × | √ | × |
7 | × | √ | √ | √ | × |
8 | √ | × | × | × | × |
9 | √ | √ | × | × | × |
10 | √ | √ | √ | √ | × |
(1)以抽取的这10名职工合格项的项数的频率代替每名职工合格项的项数的概率.
①设抽取的这10名职工中,每名职工测试合格的项数为
 ,根据上面的测试结果统计表,列出
,根据上面的测试结果统计表,列出 的分布列,并估计这120名职工的平均得分;
的分布列,并估计这120名职工的平均得分;②假设各名职工的各项测试结果相互独立,某科室有5名职工,求这5名职工中至少有4人得分不少于20分的概率;
(2)已知在测试中,测试难度的计算公式为
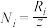 ,其中
,其中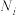 为第
为第 项测试难度,
项测试难度,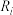 为第
为第 项合格的人数,
项合格的人数, 为参加测试的总人数.已知抽取的这10名职工每项测试合格人数及相应的实测难度如下表(表2):
为参加测试的总人数.已知抽取的这10名职工每项测试合格人数及相应的实测难度如下表(表2):表2:
| 测试项目 | 1 | 2 | 3 | 4 | 5 |
| 实测合格人数 | 8 | 8 | 7 | 7 | 2 |
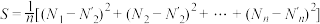 ,其中
,其中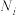 为第
为第 项的实测难度,
项的实测难度, 为第
为第 项的预测难度(
项的预测难度(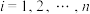 ).规定:若
).规定:若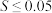 ,则称该次测试的难度预测合理,否则为不合理,测试前,预估了每个预测项目的难度,如下表(表3)所示:
,则称该次测试的难度预测合理,否则为不合理,测试前,预估了每个预测项目的难度,如下表(表3)所示:表3:
| 测试项目 | 1 | 2 | 3 | 4 | 5 |
| 预测前预估难度 | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
您最近一年使用:0次
2019-01-15更新
|
369次组卷
|
3卷引用:【市级联考】山东省滨州市2019届高三期末考试数学(理)试题
5 . 设离散型随机变量X的分布列为
X | 0 | 1 | 2 | 3 | 4 |
P | 0.2 | 0.1 | 0.1 | 0.3 | m |
求随机变量Y=|X-1|的分布列及DX.
您最近一年使用:0次
名校
6 . 小明在石家庄市某物流派送公司找到了一份派送员的工作,该公司给出了两种日薪薪酬方案.甲方案:底薪100元,每派送一单奖励1元;乙方案:底薪140元,每日前55单没有奖励,超过55单的部分每单奖励12元.
(Ⅰ)请分别求出甲、乙两种薪酬方案中日薪y(单位:元)与送货单数n的函数关系式;
(Ⅱ)根据该公司所有派送员100天的派送记录,发现派送员的日平均派送单数满足以下条件:在这100天中的派送量指标满足如图所示的直方图,其中当某天的派送量指标在(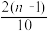 ,
,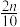 ](n=1,2,3,4,5)时,日平均派送量为50+2n单.若将频率视为概率,回答下列问题:
](n=1,2,3,4,5)时,日平均派送量为50+2n单.若将频率视为概率,回答下列问题:
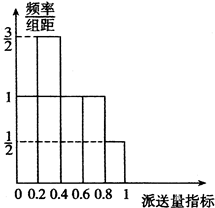
①根据以上数据,设每名派送员的日薪为X(单位:元),试分别求出甲、乙两种方案的日薪X的分布列,数学期望及方差;
②结合①中的数据,根据统计学的思想,帮助小明分析,他选择哪种薪酬方案比较合适,并说明你的理由.
(参考数据:0.62=0.36,1.42=1.9 6,2.6 2=6.76,3.42=1 1.56,3.62=12.96,4.62=21.16,15.62=243.36,20.42=416.16,44.42=1971.36)
(Ⅰ)请分别求出甲、乙两种薪酬方案中日薪y(单位:元)与送货单数n的函数关系式;
(Ⅱ)根据该公司所有派送员100天的派送记录,发现派送员的日平均派送单数满足以下条件:在这100天中的派送量指标满足如图所示的直方图,其中当某天的派送量指标在(
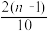 ,
,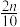 ](n=1,2,3,4,5)时,日平均派送量为50+2n单.若将频率视为概率,回答下列问题:
](n=1,2,3,4,5)时,日平均派送量为50+2n单.若将频率视为概率,回答下列问题:
①根据以上数据,设每名派送员的日薪为X(单位:元),试分别求出甲、乙两种方案的日薪X的分布列,数学期望及方差;
②结合①中的数据,根据统计学的思想,帮助小明分析,他选择哪种薪酬方案比较合适,并说明你的理由.
(参考数据:0.62=0.36,1.42=1.9 6,2.6 2=6.76,3.42=1 1.56,3.62=12.96,4.62=21.16,15.62=243.36,20.42=416.16,44.42=1971.36)
您最近一年使用:0次
名校
7 . 甲、乙两名射手在一次射击中得分为两个相互独立的随机变量ξ,η,已知甲、乙两名射手在每次射击中射中的环数大于6环,且甲射中10,9,8,7环的概率分别为0.5,3a,a,0.1,乙射中10,9,8环的概率分别为0.3,0.3,0.2.
(1)求ξ,η的分布列;
(2)求ξ,η的数学期望与方差,并以此比较甲、乙的射击技术.
(1)求ξ,η的分布列;
(2)求ξ,η的数学期望与方差,并以此比较甲、乙的射击技术.
您最近一年使用:0次
2018-08-21更新
|
1458次组卷
|
9卷引用:河北衡水市安平中学2017-2018学年高二下学期期中考试理科数学试题
河北衡水市安平中学2017-2018学年高二下学期期中考试理科数学试题辽宁省实验中学2019-2020学年高二下学期期中考试数学(理)试题黑龙江省哈尔滨市师大附中2019-2020学年高二下学期期中考试数学(理)试题(已下线)考点39 均值与方差在生活中运用(练习)-2021年高考数学复习一轮复习笔记山西省夏县第二中学2019-2020学年高二下学期期末数学试题宁夏银川市景博中学2022-2023学年高二下学期期末质量检测数学(理)试题山东学情2022-2023学年高二下学期3月联合考试数学试题B福建省漳州市第五中学2022-2023年高二下学期期中考试数学试题(已下线)专题21 离散型随机变量的均值、方差与标准差(重点突围)-【学霸满分】2022-2023学年高二数学下学期重难点专题提优训练(苏教版2019选择性必修第二册)
8 . 甲、乙两名工人加工同一种零件,两人每天加工的零件数相等,所出次品数分别为 ,
, ,且
,且 和
和 的分布列为:
的分布列为:
试比较两名工人谁的技术水平更高.
 ,
, ,且
,且 和
和 的分布列为:
的分布列为: | 0 | 1 | 2 |
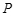 | 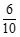 | 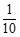 | 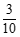 |
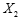 | 0 | 1 | 2 |
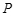 | 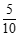 | 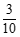 | 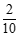 |
试比较两名工人谁的技术水平更高.
您最近一年使用:0次
名校
9 . 根据以往的经验,某工程施工期间的降水量X(单位:mm)对工期的影响如下表:
历年气象资料表明,该工程施工期间降水量X小于300,700,900的概率分别为0.3,0.7,0.9.求:工期延误天数Y的均值与方差;
| 降水量X | X<300 | 300≤X<700 | 700≤X<900 | X≥900 |
| 工期延误天数Y | 0 | 2 | 6 | 10 |
历年气象资料表明,该工程施工期间降水量X小于300,700,900的概率分别为0.3,0.7,0.9.求:工期延误天数Y的均值与方差;
您最近一年使用:0次
2018-07-21更新
|
252次组卷
|
2卷引用:【全国百强校】内蒙古乌兰察布市集宁一中(西校区)2017-2018学年高二下学期期末考试数学(理)试题
名校
10 . 从装有2只红球,2只白球和1只黑球的袋中逐一取球,已知每只球被抽取的可能性相同.
(Ⅰ)若抽取后又放回,抽3次.
(ⅰ)分别求恰2次为红球的概率及抽全三种颜色球的概率;
(ⅱ)求抽到红球次数 的数学期望及方差.
的数学期望及方差.
(Ⅱ)若抽取后不放回,写出抽完红球所需次数 的分布列.
的分布列.
(Ⅰ)若抽取后又放回,抽3次.
(ⅰ)分别求恰2次为红球的概率及抽全三种颜色球的概率;
(ⅱ)求抽到红球次数
 的数学期望及方差.
的数学期望及方差.(Ⅱ)若抽取后不放回,写出抽完红球所需次数
 的分布列.
的分布列.
您最近一年使用:0次
2018-07-20更新
|
729次组卷
|
3卷引用:辽宁省大连渤海高级中学2017-2018学年高二下学期期末考试数学(理)试题



