在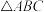 中,内角
中,内角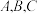 所对的边分别为
所对的边分别为 ,
, ,
, ,已知
,已知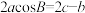 .
.
(1)求角A的大小;
(2)若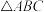 的面积
的面积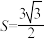 ,
,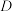 为
为 边的中点,
边的中点,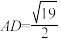 ,求
,求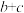 .
.
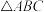 中,内角
中,内角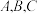 所对的边分别为
所对的边分别为 ,
, ,
, ,已知
,已知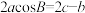 .
.(1)求角A的大小;
(2)若
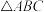 的面积
的面积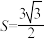 ,
,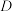 为
为 边的中点,
边的中点,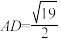 ,求
,求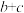 .
.
2018·全国·一模 查看更多[2]
更新时间:2018-04-25 17:02:18
|
相似题推荐
【推荐1】记 的内角
的内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,已知
,已知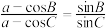 .
.
(1)若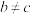 ,证明:
,证明: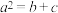 ;
;
(2)若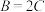 ,证明:
,证明: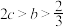 .
.
 的内角
的内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,已知
,已知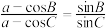 .
.(1)若
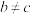 ,证明:
,证明: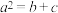 ;
;(2)若
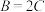 ,证明:
,证明: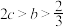 .
.
您最近半年使用:0次
解答题-问答题
|
较难
(0.4)
【推荐2】在 中,角
中,角 所对的边分别为
所对的边分别为 .
.
(1)求 的最大值;
的最大值;
(2)求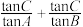 的取值范围.
的取值范围.
 中,角
中,角 所对的边分别为
所对的边分别为 .
.(1)求
 的最大值;
的最大值;(2)求
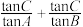 的取值范围.
的取值范围.
您最近半年使用:0次
解答题-问答题
|
较难
(0.4)
名校
解题方法
【推荐1】在锐角 中,
中,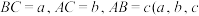 均为已知常数),.
均为已知常数),. 的外接圆,内切圆半径分别为
的外接圆,内切圆半径分别为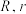 .
.
(1)求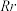 ;
;
(2)点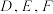 分别在线段
分别在线段 上,
上,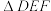 的周长为
的周长为 ,请证明:
,请证明: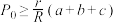 .
.
 中,
中,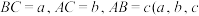 均为已知常数),.
均为已知常数),. 的外接圆,内切圆半径分别为
的外接圆,内切圆半径分别为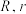 .
.(1)求
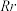 ;
;(2)点
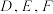 分别在线段
分别在线段 上,
上,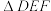 的周长为
的周长为 ,请证明:
,请证明: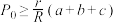 .
.
您最近半年使用:0次
解答题-问答题
|
较难
(0.4)
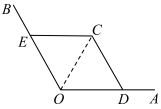
【推荐2】某公园的一个角形区域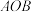 如图所示,其中
如图所示,其中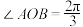 .现拟用长度为100米的隔离档板(折线
.现拟用长度为100米的隔离档板(折线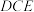 )与部分围墙(折线
)与部分围墙(折线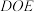 )围成一个花卉育苗区
)围成一个花卉育苗区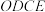 ,要求满足
,要求满足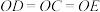 .
.
(1)设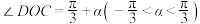 ,试用
,试用 表示
表示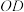 ;
;
(2)为使花卉育苗区的面积最大,应如何设计?请说明理由.
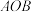 如图所示,其中
如图所示,其中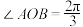 .现拟用长度为100米的隔离档板(折线
.现拟用长度为100米的隔离档板(折线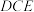 )与部分围墙(折线
)与部分围墙(折线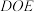 )围成一个花卉育苗区
)围成一个花卉育苗区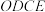 ,要求满足
,要求满足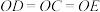 .
.
(1)设
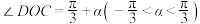 ,试用
,试用 表示
表示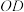 ;
;(2)为使花卉育苗区的面积最大,应如何设计?请说明理由.
您最近半年使用:0次
解答题-问答题
|
较难
(0.4)
【推荐1】已知等边三角形 中,点
中,点 为线段
为线段 上一点,且
上一点,且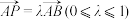 .
.
(1)若等边三角形边长为6,且 ,求
,求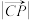 ;
;
(2)若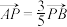 ,求
,求 的值
的值
(3)若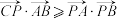 ,求实数
,求实数 的取值范围.
的取值范围.
 中,点
中,点 为线段
为线段 上一点,且
上一点,且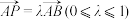 .
.(1)若等边三角形边长为6,且
 ,求
,求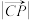 ;
;(2)若
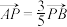 ,求
,求 的值
的值(3)若
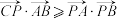 ,求实数
,求实数 的取值范围.
的取值范围.
您最近半年使用:0次
解答题-证明题
|
较难
(0.4)
名校
【推荐2】如图,已知 为平行四边形.
为平行四边形.
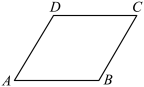
(1)若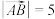 ,
,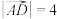 ,
, ,求
,求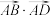 及
及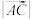 的值;
的值;
(2)记平行四边形 的面积为
的面积为 ,设
,设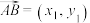 ,
,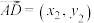 ,求证:
,求证: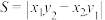
 为平行四边形.
为平行四边形.
(1)若
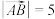 ,
,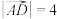 ,
, ,求
,求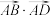 及
及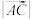 的值;
的值;(2)记平行四边形
 的面积为
的面积为 ,设
,设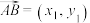 ,
,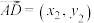 ,求证:
,求证: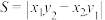
您最近半年使用:0次

 时,使得
时,使得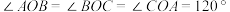 的点
的点 即为费马点;当
即为费马点;当 ,且
,且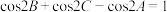
 ,设点
,设点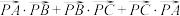 ;
;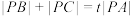 ,求实数
,求实数 的最小值.
的最小值.
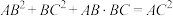 .
.
 ,求
,求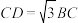 ,
,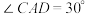 ,
, ,求∠ACB的值.
,求∠ACB的值.
 ,点
,点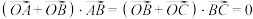 .
.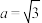 ,求
,求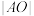 的值;
的值;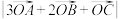 的最小值;
的最小值;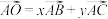 ,求
,求 的取值范围.
的取值范围.


