名校
解题方法
1 . 已知二次函数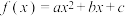 ,满足
,满足 ,且
,且 的最小值是
的最小值是 .
.
(1)求函数 的解析式;
的解析式;
(2)设函数 ,函数
,函数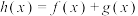 ,求函数
,求函数 在区间
在区间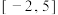 上的最值.
上的最值.
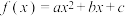 ,满足
,满足 ,且
,且 的最小值是
的最小值是 .
.(1)求函数
 的解析式;
的解析式;(2)设函数
 ,函数
,函数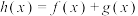 ,求函数
,求函数 在区间
在区间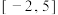 上的最值.
上的最值.
您最近一年使用:0次
名校
解题方法
2 . 已知幂函数 与一次函数
与一次函数 的图象都经过点
的图象都经过点 ,且
,且 .
.
(1)求 与
与 的解析式;
的解析式;
(2)求函数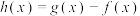 在
在 上的值域.
上的值域.
 与一次函数
与一次函数 的图象都经过点
的图象都经过点 ,且
,且 .
.(1)求
 与
与 的解析式;
的解析式;(2)求函数
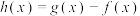 在
在 上的值域.
上的值域.
您最近一年使用:0次
解题方法
3 . 已知函数 (
( 且
且 )的图象经过点
)的图象经过点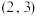 ,函数
,函数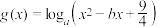 的图象经过点
的图象经过点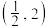 .
.
(1)求 的值;
的值;
(2)求函数 的单调递增区间.
的单调递增区间.
 (
( 且
且 )的图象经过点
)的图象经过点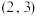 ,函数
,函数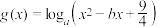 的图象经过点
的图象经过点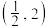 .
.(1)求
 的值;
的值;(2)求函数
 的单调递增区间.
的单调递增区间.
您最近一年使用:0次
解题方法
4 . 已知指数函数 的图像过点
的图像过点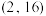 ,则
,则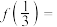
________ .
 的图像过点
的图像过点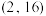 ,则
,则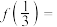
您最近一年使用:0次
解题方法
5 . 已知 是二次函数,且
是二次函数,且 ,
,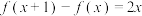 ,则
,则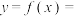
________ .
 是二次函数,且
是二次函数,且 ,
,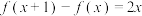 ,则
,则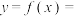
您最近一年使用:0次
解题方法
6 . 在经济学中,将产品销量为 件时的总收益称为收益函数,记为
件时的总收益称为收益函数,记为 ,相应地把
,相应地把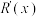 称为边际收益函数,它可以帮助企业决定最优的生产或销售水平.假设一个企业的边际收益函数
称为边际收益函数,它可以帮助企业决定最优的生产或销售水平.假设一个企业的边际收益函数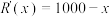 (注:经济学中涉及的函数有时是离散型函数,但仍将其看成连续函数来分析).给出下列三个结论:
(注:经济学中涉及的函数有时是离散型函数,但仍将其看成连续函数来分析).给出下列三个结论:
①当销量为1000件时,总收益最大;
②若销量为800件时,总收益为 ,则当销量增加400件时,总收益仍为
,则当销量增加400件时,总收益仍为 ;
;
③当销量从500件增加到501件时,总收益改变量的近似值为500.
其中正确结论的个数为( )
 件时的总收益称为收益函数,记为
件时的总收益称为收益函数,记为 ,相应地把
,相应地把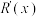 称为边际收益函数,它可以帮助企业决定最优的生产或销售水平.假设一个企业的边际收益函数
称为边际收益函数,它可以帮助企业决定最优的生产或销售水平.假设一个企业的边际收益函数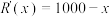 (注:经济学中涉及的函数有时是离散型函数,但仍将其看成连续函数来分析).给出下列三个结论:
(注:经济学中涉及的函数有时是离散型函数,但仍将其看成连续函数来分析).给出下列三个结论:①当销量为1000件时,总收益最大;
②若销量为800件时,总收益为
 ,则当销量增加400件时,总收益仍为
,则当销量增加400件时,总收益仍为 ;
;③当销量从500件增加到501件时,总收益改变量的近似值为500.
其中正确结论的个数为( )
| A.0 | B.1 | C.2 | D.3 |
您最近一年使用:0次
解题方法
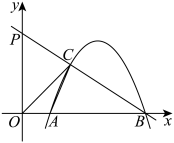
7 . 如图,开口向下的抛物线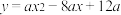 与
与 轴交于
轴交于 、
、 两点,抛物线上另有一点
两点,抛物线上另有一点 在第一象限,且使
在第一象限,且使 ,
, 的长及
的长及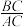 的值;
的值;
(2)设直线 与
与 轴交于
轴交于 点,点
点,点 是
是 的中点时,求直线
的中点时,求直线 和抛物线的解析式.
和抛物线的解析式.
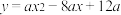 与
与 轴交于
轴交于 、
、 两点,抛物线上另有一点
两点,抛物线上另有一点 在第一象限,且使
在第一象限,且使 ,
,
 的长及
的长及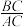 的值;
的值;(2)设直线
 与
与 轴交于
轴交于 点,点
点,点 是
是 的中点时,求直线
的中点时,求直线 和抛物线的解析式.
和抛物线的解析式.
您最近一年使用:0次
解题方法
8 . 若点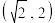 在幂函数
在幂函数 的图像上,点
的图像上,点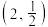 在幂函数
在幂函数 的图像上,定义
的图像上,定义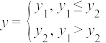 ,试求函数
,试求函数 的最大值以及在各个区间的单调性.
的最大值以及在各个区间的单调性.
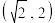 在幂函数
在幂函数 的图像上,点
的图像上,点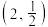 在幂函数
在幂函数 的图像上,定义
的图像上,定义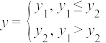 ,试求函数
,试求函数 的最大值以及在各个区间的单调性.
的最大值以及在各个区间的单调性.
您最近一年使用:0次
解题方法
9 . 某移动公司采用分段计费的方法来计算话费,月通话时间 (分钟)与相应话费
(分钟)与相应话费 (元)之间的函数图像如图所示,则
(元)之间的函数图像如图所示,则 与
与 之间的函数关系式为
之间的函数关系式为________ .
 (分钟)与相应话费
(分钟)与相应话费 (元)之间的函数图像如图所示,则
(元)之间的函数图像如图所示,则 与
与 之间的函数关系式为
之间的函数关系式为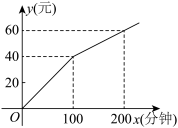
您最近一年使用:0次
解题方法
10 . 已知幂函数的图象过点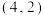 ,当
,当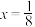 时,
时,
________ .
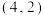 ,当
,当 时,
时,
您最近一年使用:0次



