解题方法
1 . 已知函数 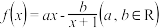 ,图象经过点
,图象经过点 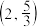 ,且
,且 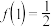 .
.
(1)求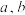 的值;
的值;
(2)用定义法证明函数 在区间
在区间 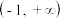 上单调递增.
上单调递增.
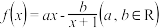 ,图象经过点
,图象经过点 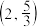 ,且
,且 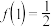 .
.(1)求
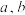 的值;
的值;(2)用定义法证明函数
 在区间
在区间 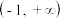 上单调递增.
上单调递增.
您最近一年使用:0次
解题方法
2 . 已知函数 是定义在
是定义在 上的奇函数,则下列函数中为偶函数的是( )
上的奇函数,则下列函数中为偶函数的是( )
 是定义在
是定义在 上的奇函数,则下列函数中为偶函数的是( )
上的奇函数,则下列函数中为偶函数的是( )A.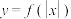 | B.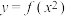 | C.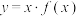 | D.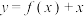 |
您最近一年使用:0次
名校
解题方法
3 . 已知函数 的定义域为
的定义域为 ,对任意正实数
,对任意正实数 ,
, 都有
都有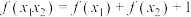 ,且当
,且当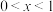 时,
时, .
.
(1)求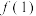 的值;
的值;
(2)试判断 的单调性,并证明;
的单调性,并证明;
(3)若 ,求
,求 的取值范围.
的取值范围.
 的定义域为
的定义域为 ,对任意正实数
,对任意正实数 ,
, 都有
都有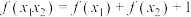 ,且当
,且当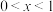 时,
时, .
.(1)求
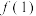 的值;
的值;(2)试判断
 的单调性,并证明;
的单调性,并证明;(3)若
 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
7日内更新
|
612次组卷
|
2卷引用:福建省福州市闽江口协作体(七校)2023-2024学年高二下学期期中联考数学试题
名校
解题方法
4 . 已知定义在 上的函数
上的函数 满足:对任意实数
满足:对任意实数 ,
, 均有
均有 ,则下列结论中,错误的是( )
,则下列结论中,错误的是( )
 上的函数
上的函数 满足:对任意实数
满足:对任意实数 ,
, 均有
均有 ,则下列结论中,错误的是( )
,则下列结论中,错误的是( )A.存在 使 使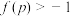 且 且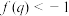 |
B. 可能为常数函数 可能为常数函数 |
C.若 ,则 ,则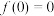 |
D.若 ,且 ,且 时, 时,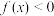 ,则 ,则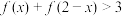 解集为 解集为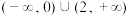 |
您最近一年使用:0次
名校
解题方法
5 . 已知函数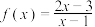 .
.
(1)证明: 在
在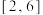 上单调递增;
上单调递增;
(2)求 在
在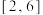 上的最大值与最小值.
上的最大值与最小值.
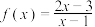 .
.(1)证明:
 在
在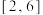 上单调递增;
上单调递增;(2)求
 在
在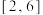 上的最大值与最小值.
上的最大值与最小值.
您最近一年使用:0次
解题方法
6 . 已知幂函数的图像经过点 .
.
(1)求幂函数解析式;
(2)求证:幂函数在区间 上是严格增函数.
上是严格增函数.
 .
.(1)求幂函数解析式;
(2)求证:幂函数在区间
 上是严格增函数.
上是严格增函数.
您最近一年使用:0次
名校
解题方法
7 . 定义在 上的函数
上的函数 满足
满足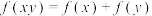 ,
,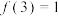 ,且
,且 时,
时, .
.
(1)求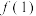 ;
;
(2)判断 在
在 上的单调性并证明;
上的单调性并证明;
(3)若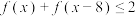 ,求
,求 的取值范围.
的取值范围.
 上的函数
上的函数 满足
满足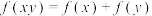 ,
,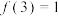 ,且
,且 时,
时, .
.(1)求
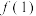 ;
;(2)判断
 在
在 上的单调性并证明;
上的单调性并证明;(3)若
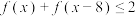 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
8 . 求证:方程 没有整数解.
没有整数解.
 没有整数解.
没有整数解.
您最近一年使用:0次
解题方法
9 . 已知函数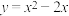 ,小明同学说,“开口向上,对称轴为
,小明同学说,“开口向上,对称轴为 ,对称轴左边是严格减函数,右边是严格增函数”,你能总结一般的一元二次函数的单调性规律,并证明.
,对称轴左边是严格减函数,右边是严格增函数”,你能总结一般的一元二次函数的单调性规律,并证明.
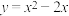 ,小明同学说,“开口向上,对称轴为
,小明同学说,“开口向上,对称轴为 ,对称轴左边是严格减函数,右边是严格增函数”,你能总结一般的一元二次函数的单调性规律,并证明.
,对称轴左边是严格减函数,右边是严格增函数”,你能总结一般的一元二次函数的单调性规律,并证明.
您最近一年使用:0次
解题方法
10 . 用函数单调性定义证明函数 是在区间
是在区间 上的严格减函数.
上的严格减函数.
 是在区间
是在区间 上的严格减函数.
上的严格减函数.
您最近一年使用:0次



