2023高三·全国·专题练习
1 . 已知函数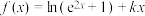 是偶函数.
是偶函数.
(1)求实数k的值.
(2)当 时,函数
时,函数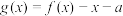 存在零点,求实数a的取值范围.
存在零点,求实数a的取值范围.
(3)函数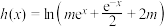 (
( 且
且 ),函数
),函数 有2个零点,求实数m的取值范围.
有2个零点,求实数m的取值范围.
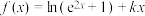 是偶函数.
是偶函数.(1)求实数k的值.
(2)当
 时,函数
时,函数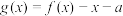 存在零点,求实数a的取值范围.
存在零点,求实数a的取值范围.(3)函数
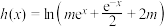 (
( 且
且 ),函数
),函数 有2个零点,求实数m的取值范围.
有2个零点,求实数m的取值范围.
您最近一年使用:0次
名校
解题方法
2 . 已知函数 与
与 的定义域为R,若对任意区间
的定义域为R,若对任意区间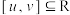 ,存在
,存在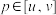 且
且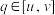 ,使
,使 ,则
,则 是
是 的生成函数.
的生成函数.
(1)求证: 是
是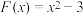 的生成函数;
的生成函数;
(2)若 是
是 的生成函数,判断并证明
的生成函数,判断并证明 的单调性;
的单调性;
(3)若 是
是 的生成函数,实数
的生成函数,实数 ,求
,求 的一个生成函数.
的一个生成函数.
 与
与 的定义域为R,若对任意区间
的定义域为R,若对任意区间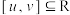 ,存在
,存在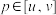 且
且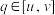 ,使
,使 ,则
,则 是
是 的生成函数.
的生成函数.(1)求证:
 是
是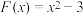 的生成函数;
的生成函数;(2)若
 是
是 的生成函数,判断并证明
的生成函数,判断并证明 的单调性;
的单调性;(3)若
 是
是 的生成函数,实数
的生成函数,实数 ,求
,求 的一个生成函数.
的一个生成函数.
您最近一年使用:0次
2023-05-05更新
|
557次组卷
|
4卷引用:上海交通大学附属中学2022-2023学年高一下学期期中数学试题
上海交通大学附属中学2022-2023学年高一下学期期中数学试题湖南省长沙市明德中学2022-2023学年高一下学期5月月考数学试题(已下线)第3课时 课后 函数的单调性(完成)(已下线)5.2.2 函数的单调性-数学同步精品课堂(沪教版2020必修第一册)
名校
解题方法
3 . 已知函数 的定义域是
的定义域是 ,且
,且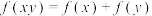 ,当
,当 时,
时, ,
, ,则下列说法正确的是( )
,则下列说法正确的是( )
 的定义域是
的定义域是 ,且
,且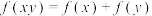 ,当
,当 时,
时, ,
, ,则下列说法正确的是( )
,则下列说法正确的是( )A.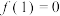 |
B.函数 在 在 上是减函数 上是减函数 |
C. |
D.不等式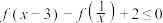 的解集为 的解集为 |
您最近一年使用:0次
2023-02-03更新
|
1354次组卷
|
28卷引用:2023版 北师大版(2019) 必修第一册 突围者 第二章 第三节 函数的单调性和最值
2023版 北师大版(2019) 必修第一册 突围者 第二章 第三节 函数的单调性和最值重庆市开州区临江中学2023届高三上学期入学考试数学试题福建省厦门市厦门外国语学校2022-2023学年高一上学期期中考试数学试题浙江省宁波市鄞州中学2022-2023学年高一上学期期中数学试题河南省驻马店市第二高级中学2022-2023学年高一上学期第一次调研考试数学试题广东省清远市四校2022-2023学年高一上学期联合学业质量检测数学试题河南省杞县高中2022-2023学年高一上学期期中网课检测数学试卷江西省上饶市2022-2023学年高一上学期期末教学质量测试数学试题湖北省十堰市天河英才高中2022-2023学年高一上学期12月月考数学试题安徽省黄山市屯溪第一中学2022-2023学年高一上学期期中数学试题2.3 函数的单调性和最值同步练习-2022-2023学年高一上学期数学北师大版(2019)必修第一册辽宁省抚顺市第一中学2022-2023学年高一上学期期末数学试题(已下线)3.2.1 函数的单调性(精练)-《一隅三反》湖南省株洲市第二中学2023-2024学年高一上学期第一次适应性检测数学试题3.2.1 单调性与最大(小)值练习黑龙江省绥化市绥棱县第一中学2022-2023学年高一下学期开学考试数学试题福建省连城县第一中学2023-2024学年高一上学期10月月考数学试题山东省泰安市宁阳县第四中学2023-2024学年高三上学期10月月考数学试题(已下线)第三章 函数的概念与性质(压轴题专练)-速记·巧练(人教A版2019必修第一册)山东省泰安市宁阳县2023-2024学年高三上学期第一次阶段性测试数学试题吉林省辽源市第五中学校2023-2024学年高一上学期期中数学试题河北省曲阳县第一高级中学2023-2024学年高一上学期期中数学试题福建省福州市鼓山中学2023-2024学年高一上学期10月月考数学试题福建省莆田第六中学2023-2024学年高一上学期10月校本作业(月考)数学试卷A(已下线)湖南省长沙市长郡中学2024届高三上学期月考(二)数学试题变式题11-14甘肃省武威市民勤县第一中学2023-2024学年高一上学期第二次月考数学试题云南省昆明市禄劝彝族苗族自治县第一中学2023-2024学年高一下学期3月月考数学试题(已下线)湖南省长沙市四县区2024届高三下学期3月调研考试数学试题变式题11-15
解题方法
4 . 设函数 的定义域为D,集合
的定义域为D,集合 ,若存在非零实数t使得对任意
,若存在非零实数t使得对任意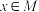 都有
都有 ,且
,且 ,则称
,则称 为M上的t-增长函数.
为M上的t-增长函数.
(1)已知函数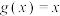 ,判断
,判断 是否为区间
是否为区间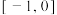 上的
上的 -增长函数,并说明理由;
-增长函数,并说明理由;
(2)已知函数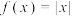 ,且
,且 是区间
是区间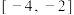 上的n-增长函数,求正整数n的最小值;
上的n-增长函数,求正整数n的最小值;
(3)如果 是定义域为R的奇函数,当
是定义域为R的奇函数,当 时,
时,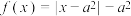 ,且
,且 为R上的4-增长函数,求实数a的取值范围.
为R上的4-增长函数,求实数a的取值范围.
 的定义域为D,集合
的定义域为D,集合 ,若存在非零实数t使得对任意
,若存在非零实数t使得对任意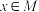 都有
都有 ,且
,且 ,则称
,则称 为M上的t-增长函数.
为M上的t-增长函数.(1)已知函数
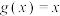 ,判断
,判断 是否为区间
是否为区间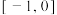 上的
上的 -增长函数,并说明理由;
-增长函数,并说明理由;(2)已知函数
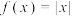 ,且
,且 是区间
是区间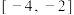 上的n-增长函数,求正整数n的最小值;
上的n-增长函数,求正整数n的最小值;(3)如果
 是定义域为R的奇函数,当
是定义域为R的奇函数,当 时,
时,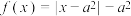 ,且
,且 为R上的4-增长函数,求实数a的取值范围.
为R上的4-增长函数,求实数a的取值范围.
您最近一年使用:0次
解题方法
5 . 利用函数图像可知 在
在 内有
内有______ 个解.
 在
在 内有
内有
您最近一年使用:0次
2023-01-04更新
|
537次组卷
|
2卷引用:沪教版(2020) 必修第二册 单元训练 第7章 函数y=Asin(ωx+ψ)的图像、正切函数的图像与性质(B卷)
6 . 证明:方程 没有整数解.
没有整数解.
 没有整数解.
没有整数解.
您最近一年使用:0次
7 . 设定义在R上的函数 满足
满足 ,且对任意x,
,且对任意x,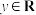 都有
都有 ,则
,则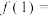
______ ;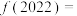
______ .
 满足
满足 ,且对任意x,
,且对任意x,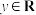 都有
都有 ,则
,则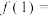
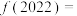
您最近一年使用:0次
2022-12-15更新
|
451次组卷
|
4卷引用:黑龙江省绥化市绥棱县2022-2023学年高一上学期期中数学试题
黑龙江省绥化市绥棱县2022-2023学年高一上学期期中数学试题辽宁省朝阳市凌源市2022-2023学年高一上学期12月月考数学试题(已下线)【第二课】3.1.1函数的概念(已下线)第五章 函数的概念、性质及应用(压轴题专练)-单元速记·巧练(沪教版2020必修第一册)
名校
解题方法
8 . 已知函数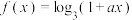 ,
,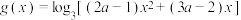 ,
, .
.
(1)若 ,求不等式
,求不等式 的解集;
的解集;
(2)已知函数 ,且方程
,且方程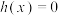 有唯一实数解,求实数
有唯一实数解,求实数 的取值范围.
的取值范围.
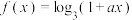 ,
,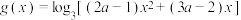 ,
, .
.(1)若
 ,求不等式
,求不等式 的解集;
的解集;(2)已知函数
 ,且方程
,且方程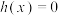 有唯一实数解,求实数
有唯一实数解,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2022-11-30更新
|
1303次组卷
|
5卷引用:黑龙江省齐齐哈尔市2020-2021学年高二下学期期末考试数学(文)试题
黑龙江省齐齐哈尔市2020-2021学年高二下学期期末考试数学(文)试题(已下线)专题4.11 指数函数、对数函数的综合应用大题专项训练(30道)-2021-2022学年高一数学举一反三系列(人教A版2019必修第一册)广西桂林市第十八中学2022-2023学年高一上学期期中考试数学试题江苏省宿迁市泗阳县实验高级中学2022-2023学年高一上学期期末数学试题四川省成都市龙泉驿区东竞高级中学2023-2024学年高一上学期12月月考数学试题
名校
解题方法
9 . 若集合A具有以下性质,则称集合A是“好集”:①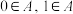 ;②若
;②若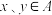 ,则
,则 ,且
,且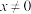 时,
时,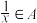 .
.
(1)分别判断集合 ,有理数集
,有理数集 是否是“好集”,并说明理由;
是否是“好集”,并说明理由;
(2)设集合 是“好集”,求证:若
是“好集”,求证:若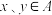 ,则
,则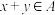 ;
;
(3)对任意的一个“好集”A,判断下面命题的真假,并说明理由;命题:若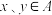 ,则必有
,则必有 .
.
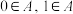 ;②若
;②若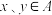 ,则
,则 ,且
,且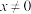 时,
时,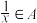 .
.(1)分别判断集合
 ,有理数集
,有理数集 是否是“好集”,并说明理由;
是否是“好集”,并说明理由;(2)设集合
 是“好集”,求证:若
是“好集”,求证:若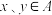 ,则
,则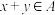 ;
;(3)对任意的一个“好集”A,判断下面命题的真假,并说明理由;命题:若
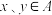 ,则必有
,则必有 .
.
您最近一年使用:0次
解题方法
10 . 形如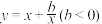 的函数的图象很像两个“丿”,人们习惯称此类函数为“两撇函数”.它具有如下性质:① 该函数为奇函数;② 该函数在
的函数的图象很像两个“丿”,人们习惯称此类函数为“两撇函数”.它具有如下性质:① 该函数为奇函数;② 该函数在 上单调递增.
上单调递增.
(1)当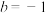 时,请举例说明
时,请举例说明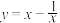 在
在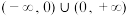 上不是增函数;
上不是增函数;
(2)已知 ,设
,设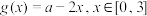 .若
.若 ,
,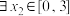 ,使得
,使得 ,求实数a的取值范围.
,求实数a的取值范围.
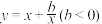 的函数的图象很像两个“丿”,人们习惯称此类函数为“两撇函数”.它具有如下性质:① 该函数为奇函数;② 该函数在
的函数的图象很像两个“丿”,人们习惯称此类函数为“两撇函数”.它具有如下性质:① 该函数为奇函数;② 该函数在 上单调递增.
上单调递增.(1)当
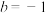 时,请举例说明
时,请举例说明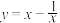 在
在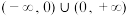 上不是增函数;
上不是增函数;(2)已知
 ,设
,设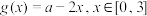 .若
.若 ,
,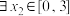 ,使得
,使得 ,求实数a的取值范围.
,求实数a的取值范围.
您最近一年使用:0次
2022-11-12更新
|
327次组卷
|
3卷引用:河北省张家口市2022-2023学年高一上学期期中数学试题
河北省张家口市2022-2023学年高一上学期期中数学试题2.3函数的单调性和最值测试卷-2022-2023学年高一上学期数学北师大版(2019)必修第一册(已下线)模块五 专题1 期中重组卷(河北)



