1 . 若函数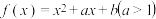 的值域为
的值域为 ,则
,则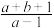 的最小值为
的最小值为________ .
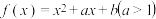 的值域为
的值域为 ,则
,则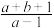 的最小值为
的最小值为
您最近一年使用:0次
名校
解题方法
2 . 已知函数 ,
, .
.
(1)若对任意 ,不等式
,不等式 恒成立,求m的取值范围;
恒成立,求m的取值范围;
(2)若对任意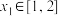 ,存在
,存在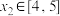 ,使得
,使得 ,求m的取值范围;
,求m的取值范围;
(3)若 ,对任意
,对任意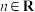 ,总存在
,总存在 ,使得不等式
,使得不等式 成立,求实数k的取值范围.
成立,求实数k的取值范围.
 ,
, .
.(1)若对任意
 ,不等式
,不等式 恒成立,求m的取值范围;
恒成立,求m的取值范围;(2)若对任意
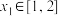 ,存在
,存在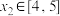 ,使得
,使得 ,求m的取值范围;
,求m的取值范围;(3)若
 ,对任意
,对任意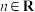 ,总存在
,总存在 ,使得不等式
,使得不等式 成立,求实数k的取值范围.
成立,求实数k的取值范围.
您最近一年使用:0次
2023-02-27更新
|
2168次组卷
|
9卷引用:浙江省湖州市2022-2023学年高一上学期2月期末数学试题
浙江省湖州市2022-2023学年高一上学期2月期末数学试题(已下线)专题2.5 一元二次函数、方程和不等式全章八类必考压轴题-举一反三系列(已下线)高一上学期第一次月考解答题压轴题50题专练-举一反三系列重庆市西南大学附属中学校2023-2024学年高一上学期9月定时检测(一)数学试题(已下线)高一上学期期中考试解答题压轴题50题专练-举一反三系列广东省惠州市惠阳区第一中学高中部2023-2024学年高一上学期期中数学试题(已下线)高一上学期期末复习【第二章 一元二次函数、方程和不等式】(拔尖篇)-举一反三系列(已下线)模块五 专题4 重组综合练(浙江)期末终极研习室(已下线)高一上学期期末考试解答题压轴题50题专练-举一反三系列
名校
解题方法
3 . 已知函数 的定义域为区间[m,n],其中
的定义域为区间[m,n],其中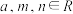 ,若f(x)的值域为[-4,4],则
,若f(x)的值域为[-4,4],则 的取值范围是( )
的取值范围是( )
 的定义域为区间[m,n],其中
的定义域为区间[m,n],其中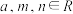 ,若f(x)的值域为[-4,4],则
,若f(x)的值域为[-4,4],则 的取值范围是( )
的取值范围是( )A.[4,4 ] ] | B.[2 ,8 ,8 ] ] | C.[4,8 ] ] | D.[4 ,8] ,8] |
您最近一年使用:0次
2022-01-21更新
|
2234次组卷
|
6卷引用:浙江省台州市2021-2022学年高一上学期期末数学试题
浙江省台州市2021-2022学年高一上学期期末数学试题浙江省衢州市乐成寄宿中学2022-2023学年高一上学期12月月考数学试题江苏省南通市启东中学2022-2023学年高一上学期期中数学试题(已下线)高一上学期第一次月考选择题压轴题50题专练-举一反三系列(已下线)专题05 二次函数与一元二次不等式压轴题-【常考压轴题】(已下线)专题02 一元二次函数、方程和不等式3-2024年高一数学寒假作业单元合订本
名校
解题方法
4 . 设二次函数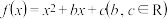 .
.
(1)若 ,且
,且 在
在 上的最大值为
上的最大值为 ,求函数
,求函数 的解析式;
的解析式;
(2)若对任意的实数b,都存在实数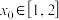 ,使得不等式
,使得不等式 成立,求实数c的取值范围.
成立,求实数c的取值范围.
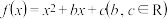 .
.(1)若
 ,且
,且 在
在 上的最大值为
上的最大值为 ,求函数
,求函数 的解析式;
的解析式;(2)若对任意的实数b,都存在实数
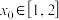 ,使得不等式
,使得不等式 成立,求实数c的取值范围.
成立,求实数c的取值范围.
您最近一年使用:0次
2022-01-12更新
|
1286次组卷
|
10卷引用:2015年6月浙江省普通高中学业水平模拟测试数学试卷
2015年6月浙江省普通高中学业水平模拟测试数学试卷(已下线)【新东方】高中数学20210527-001【2021】【高二下】浙江省金华市义乌市2019-2020学年高一下学期期末数学试题浙江省杭州学军中学西溪校区2022-2023学年高一上学期期中数学试题(已下线)高中数学-高一上-58(已下线)第3章 函数概念与性质(巩固篇)-2021-2022学年高一数学单元过关卷(人教A版2019必修第一册)广东省阳江市2021-2022学年高二上学期期末数学试题(已下线)专题05 二次函数与一元二次不等式压轴题-【常考压轴题】(已下线)模块三 专题1 不等式恒成立、能成立问题(已下线)重难点02 一元二次不等式恒成立、能成立问题【六大题型】
5 . 已知函数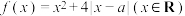 .
.
(Ⅰ)存在实数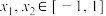 使得
使得 成立,求实数
成立,求实数 的取值范围;
的取值范围;
(Ⅱ)对任意的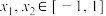 都有
都有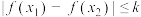 成立,求实数
成立,求实数 的最小值.
的最小值.
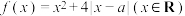 .
.(Ⅰ)存在实数
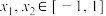 使得
使得 成立,求实数
成立,求实数 的取值范围;
的取值范围;(Ⅱ)对任意的
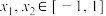 都有
都有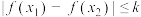 成立,求实数
成立,求实数 的最小值.
的最小值.
您最近一年使用:0次
解题方法
6 . 设a为正数,函数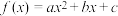 满足
满足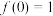 且
且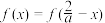
(1)若f(1)=1,求f(x);
(2)设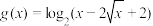 ,若对任意实数t,总存在x1、x2∈[t-1,t+1],使得f(x1)-f(x2)≥g(x3)-g(x4)对所有x3,x4∈
,若对任意实数t,总存在x1、x2∈[t-1,t+1],使得f(x1)-f(x2)≥g(x3)-g(x4)对所有x3,x4∈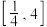 都成立,求a的取值范围.
都成立,求a的取值范围.
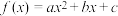 满足
满足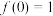 且
且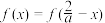
(1)若f(1)=1,求f(x);
(2)设
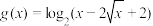 ,若对任意实数t,总存在x1、x2∈[t-1,t+1],使得f(x1)-f(x2)≥g(x3)-g(x4)对所有x3,x4∈
,若对任意实数t,总存在x1、x2∈[t-1,t+1],使得f(x1)-f(x2)≥g(x3)-g(x4)对所有x3,x4∈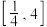 都成立,求a的取值范围.
都成立,求a的取值范围.
您最近一年使用:0次
2020-08-07更新
|
2253次组卷
|
4卷引用:【新东方】双师87
(已下线)【新东方】双师87广东省广州市2019-2020学年广雅、执信、二中、六中四校高一下学期期末联考数学试题(已下线)专题07 一元二次函数、方程和不等式中的压轴题(一)-【尖子生专用】2021-2022学年高一数学考点培优训练(人教A版2019必修第一册)广东省广州市六中、二中、广雅、省实、执信五校2022-2023学年高一下学期期末联考数学试题
名校
解题方法
7 . 已知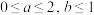 ,函数
,函数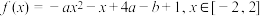 .
.
(1)讨论 的单调性;
的单调性;
(2)设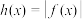 ,若
,若 的最大值为
的最大值为 ,求
,求 的取值范围.
的取值范围.
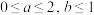 ,函数
,函数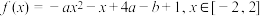 .
. (1)讨论
 的单调性;
的单调性;(2)设
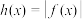 ,若
,若 的最大值为
的最大值为 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2020-02-24更新
|
1780次组卷
|
2卷引用:浙江省温州市2019-2020学年高一上学期期末数学试题(A)



