名校
解题方法
1 . 某考试分为笔试和面试两个部分,每个部分的成绩分为A,B,C三个等级,其中A等级得3分、B等级得2分、C等级得1分.甲在笔试中获得A等级、B等级、C等级的概率分别为 ,
, ,
, ,在面试中获得A等级、B等级、C等级的概率分别为
,在面试中获得A等级、B等级、C等级的概率分别为 ,
, ,
, ,甲笔试的结果和面试的结果相互独立.
,甲笔试的结果和面试的结果相互独立.
(1)求甲在笔试和面试中恰有一次获得A等级的概率;
(2)求甲笔试和面试的得分之和X的分布列与期望.
 ,
, ,
, ,在面试中获得A等级、B等级、C等级的概率分别为
,在面试中获得A等级、B等级、C等级的概率分别为 ,
, ,
, ,甲笔试的结果和面试的结果相互独立.
,甲笔试的结果和面试的结果相互独立.(1)求甲在笔试和面试中恰有一次获得A等级的概率;
(2)求甲笔试和面试的得分之和X的分布列与期望.
您最近一年使用:0次
昨日更新
|
677次组卷
|
6卷引用:专题03 随机变量的分布列--高二期末考点大串讲(人教B版2019选择性必修第二册)
名校
解题方法
2 . 为丰富和活跃学校教师业余文化生活,提高教师身体素质,展现教师自我风采,增进教师沟通交流,阳泉一中举办了2024年度第一届青年教师团建暨羽毛球比赛活动,已知其决赛在小胡和小张之间进行,每场比赛均能分出胜负,已知该学校为本次决赛提供了1000元奖金,并规定:若其中一人赢的场数先达到4场,则比赛终止,同时该人获得全部奖金;若比赛意外终止时无人先赢4场,则按照比赛继续进行各自赢得全部奖金的概率之比给两人分配奖金.若每场比赛小胡赢的概率为 ,每场比赛相互独立.
,每场比赛相互独立.
(1)在已进行的5场比赛中小胡赢了3场,若比赛继续进行到有人先赢4场,求小胡赢得全部奖金的概率;
(2)若比赛进行了5场时终止(含自然终止与意外终止),记小胡获得奖金数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
 ,每场比赛相互独立.
,每场比赛相互独立.(1)在已进行的5场比赛中小胡赢了3场,若比赛继续进行到有人先赢4场,求小胡赢得全部奖金的概率;
(2)若比赛进行了5场时终止(含自然终止与意外终止),记小胡获得奖金数为
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
您最近一年使用:0次
名校
3 . 水平相当的甲、乙、丙三人进行乒乓球擂台赛,每轮比赛都采用3局2胜制(即先贏2局者胜),首轮由甲乙两人开始,丙轮空;第二轮由首轮的胜者与丙之间进行,首轮的负者轮空,依照这样的规则无限地继续下去.
(1)求甲在第三轮获胜的条件下,第二轮也获胜的概率;
(2)求第 轮比赛甲轮空的概率;
轮比赛甲轮空的概率;
(3)按照以上规则,求前六轮比赛中甲获胜局数的期望.
(1)求甲在第三轮获胜的条件下,第二轮也获胜的概率;
(2)求第
 轮比赛甲轮空的概率;
轮比赛甲轮空的概率;(3)按照以上规则,求前六轮比赛中甲获胜局数的期望.
您最近一年使用:0次
名校
解题方法
4 . 某单位为了丰富群众文化生活,提高对本行业的认同度,在“五一国际劳动节”期间举行了“本行业知识有奖竞答活动”,活动规则如下:每位参加活动的职工都有两轮回答问题的机会.第一轮:参加活动的职工先抛掷一枚骰子1次,掷出1点或2点,则可回答1个低阶问题,回答正确获得奖金20元,回答错误获得奖金10元;掷出3点,4点,5点,6点,则可回答一个高阶问题,回答正确获得奖金40元,回答错误获得奖金20元.第二轮:若第一轮回答正确,则第二轮回答一个高阶问题,回答正确可获得资金60元,回答错误可获得奖金30元;若第一轮回答错误,则第二轮回答一个低阶问题,回答正确可获得资金30元,回答错误可获得奖金20元.职工甲参加活动,已知他每一轮回答高阶问题的正确率均为 ,回答低阶问题的正确率均为
,回答低阶问题的正确率均为 ;每轮奖金累积,求解下列问题:
;每轮奖金累积,求解下列问题:
(1)求第一轮甲回答问题后获得20元奖金的概率;
(2)求在第一轮中甲已获得奖金20元的条件下,甲两轮累计获得奖金不低于50元的概率.
 ,回答低阶问题的正确率均为
,回答低阶问题的正确率均为 ;每轮奖金累积,求解下列问题:
;每轮奖金累积,求解下列问题:(1)求第一轮甲回答问题后获得20元奖金的概率;
(2)求在第一轮中甲已获得奖金20元的条件下,甲两轮累计获得奖金不低于50元的概率.
您最近一年使用:0次
名校
解题方法
5 . RoboMaster机甲大师高校系列赛(RMU,RoboMasterUniversitySeries),作为全国大学生机器人大赛旗下赛事之一,是专为全球科技爱好者打造的机器人竞技与学术交流平台,在“3V3”对抗赛中,甲、乙、丙三支高校队在每轮对抗赛中,乙胜丙的概率为 ,甲胜丙的概率为
,甲胜丙的概率为 ,每轮对抗赛没有平局且成绩互不影响.
,每轮对抗赛没有平局且成绩互不影响.
(1)若乙与丙进行3轮对抗赛,求丙在对抗赛中至少有2轮胜出的概率;
(2)若甲与丙进行对抗,甲胜2轮就停止,否则开始新一轮对抗,但对抗不超过5轮,求对抗赛轮数 的分布列与数学期望.
的分布列与数学期望.
 ,甲胜丙的概率为
,甲胜丙的概率为 ,每轮对抗赛没有平局且成绩互不影响.
,每轮对抗赛没有平局且成绩互不影响.(1)若乙与丙进行3轮对抗赛,求丙在对抗赛中至少有2轮胜出的概率;
(2)若甲与丙进行对抗,甲胜2轮就停止,否则开始新一轮对抗,但对抗不超过5轮,求对抗赛轮数
 的分布列与数学期望.
的分布列与数学期望.
您最近一年使用:0次
名校
解题方法
6 . 为培养学生的阅读习惯,某学校规定所有学生每天在校阅读时长不得少于1小时.若认为每天在校阅读的时长不少于1小时为达标,达到2小时的学生为“阅读之星”.假设该校学生每天在校阅读时长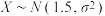 (
( 的单位:小时),达标学生是“阅读之星”的概率为
的单位:小时),达标学生是“阅读之星”的概率为 .
.
(1)从该校学生中随机选出1人,求达标的概率;
(2)为进一步了解该校学生不达标是否与性别有关,随机调查了90名学生,其中男生占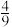 ,已知不达标的人数恰是期望值,且不达标的学生中男生占
,已知不达标的人数恰是期望值,且不达标的学生中男生占 ,是否有99%的把握认为不达标与性别有关?
,是否有99%的把握认为不达标与性别有关?
附:参考公式: ,其中
,其中 .
.
参考数据:
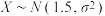 (
( 的单位:小时),达标学生是“阅读之星”的概率为
的单位:小时),达标学生是“阅读之星”的概率为 .
.(1)从该校学生中随机选出1人,求达标的概率;
(2)为进一步了解该校学生不达标是否与性别有关,随机调查了90名学生,其中男生占
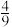 ,已知不达标的人数恰是期望值,且不达标的学生中男生占
,已知不达标的人数恰是期望值,且不达标的学生中男生占 ,是否有99%的把握认为不达标与性别有关?
,是否有99%的把握认为不达标与性别有关?附:参考公式:
 ,其中
,其中 .
.参考数据:
| 3.841 | 5.024 | 6.635 | 10.828 |
| 0.050 | 0.025 | 0.010 | 0.001 |
您最近一年使用:0次
名校
7 . 某公司为监督检查下属的甲、乙两条生产线所生产产品的质量,分别从甲、乙两条生产线出库的产品中各随机抽取了100件产品,并对所抽取产品进行检验,检验后发现,甲生产线的合格品占八成、优等品占两成,乙生产线的合格品占九成、优等品占一成(合格品与优等品间无包含关系).
(1)用分层随机抽样的方法从样品的优等品中抽取6件产品,在这6件产品中随机抽取2件,记这2件产品中来自甲生产线的产品个数有 个,求
个,求 的分布列与数学期望;
的分布列与数学期望;
(2)消费者对该公司产品的满意率为 ,随机调研5位购买过该产品的消费者,记对该公司产品满意的人数有
,随机调研5位购买过该产品的消费者,记对该公司产品满意的人数有 人,求至少有3人满意的概率及
人,求至少有3人满意的概率及 的数学期望与方差.
的数学期望与方差.
(1)用分层随机抽样的方法从样品的优等品中抽取6件产品,在这6件产品中随机抽取2件,记这2件产品中来自甲生产线的产品个数有
 个,求
个,求 的分布列与数学期望;
的分布列与数学期望;(2)消费者对该公司产品的满意率为
 ,随机调研5位购买过该产品的消费者,记对该公司产品满意的人数有
,随机调研5位购买过该产品的消费者,记对该公司产品满意的人数有 人,求至少有3人满意的概率及
人,求至少有3人满意的概率及 的数学期望与方差.
的数学期望与方差.
您最近一年使用:0次
名校
8 . 某校组织全校数学老师参加解题大赛,对于大赛中的最后一个解答题,甲得满分的概率为0.8,乙得满分的概率为0.7,记事件A:甲最后一个解答题得满分,事件B:乙最后一个解答题得满分.
(1)求甲、乙两人最后一个解答题都得满分的概率;
(2)求甲、乙恰有一人最后一个解答题得满分的概率.
(1)求甲、乙两人最后一个解答题都得满分的概率;
(2)求甲、乙恰有一人最后一个解答题得满分的概率.
您最近一年使用:0次
2024高一·全国·专题练习
9 . 下面所给出的两个事件 与
与 相互独立吗?
相互独立吗?
(1)抛掷一枚骰子,事件 “出现1点”,事件
“出现1点”,事件 “出现2点”;
“出现2点”;
(2)先后抛掷两枚质地均匀的硬币,事件 “第一枚出现正面”,事件
“第一枚出现正面”,事件 “第二枚出现反面”;
“第二枚出现反面”;
(3)在装有2红1绿三个除颜色外完全相同的小球的口袋中,任取一个小球,观察颜色后放回袋中,事件 “第一次取到绿球”,
“第一次取到绿球”, “第二次取到绿球”.
“第二次取到绿球”.
 与
与 相互独立吗?
相互独立吗?(1)抛掷一枚骰子,事件
 “出现1点”,事件
“出现1点”,事件 “出现2点”;
“出现2点”;(2)先后抛掷两枚质地均匀的硬币,事件
 “第一枚出现正面”,事件
“第一枚出现正面”,事件 “第二枚出现反面”;
“第二枚出现反面”;(3)在装有2红1绿三个除颜色外完全相同的小球的口袋中,任取一个小球,观察颜色后放回袋中,事件
 “第一次取到绿球”,
“第一次取到绿球”, “第二次取到绿球”.
“第二次取到绿球”.
您最近一年使用:0次
10 . 已知 ,
, ,
, ,
, 四名选手参加某项比赛,其中
四名选手参加某项比赛,其中 ,
, 为种子选手,
为种子选手, ,
, 为非种子选手,种子选手对非种子选手种子选手获胜的概率为
为非种子选手,种子选手对非种子选手种子选手获胜的概率为 ,种子选手之间的获胜的概率为
,种子选手之间的获胜的概率为 ,非种子选手之间获胜的概率为
,非种子选手之间获胜的概率为 .比赛规则:第一轮两两对战,胜者进入第二轮,负者淘汰;第二轮的胜者为冠军.
.比赛规则:第一轮两两对战,胜者进入第二轮,负者淘汰;第二轮的胜者为冠军.
(1)若你是主办方,则第一轮选手的对战安排一共有多少不同的方案?
(2)选手 与选手
与选手 相遇的概率为多少?
相遇的概率为多少?
(3)以下两种方案,哪一种种子选手夺冠的概率更大?
方案一:第一轮比赛种子选手与非种子选手比赛;
方案二:第一轮比赛种子选手与种子选手比赛.
 ,
, ,
, ,
, 四名选手参加某项比赛,其中
四名选手参加某项比赛,其中 ,
, 为种子选手,
为种子选手, ,
, 为非种子选手,种子选手对非种子选手种子选手获胜的概率为
为非种子选手,种子选手对非种子选手种子选手获胜的概率为 ,种子选手之间的获胜的概率为
,种子选手之间的获胜的概率为 ,非种子选手之间获胜的概率为
,非种子选手之间获胜的概率为 .比赛规则:第一轮两两对战,胜者进入第二轮,负者淘汰;第二轮的胜者为冠军.
.比赛规则:第一轮两两对战,胜者进入第二轮,负者淘汰;第二轮的胜者为冠军.(1)若你是主办方,则第一轮选手的对战安排一共有多少不同的方案?
(2)选手
 与选手
与选手 相遇的概率为多少?
相遇的概率为多少?(3)以下两种方案,哪一种种子选手夺冠的概率更大?
方案一:第一轮比赛种子选手与非种子选手比赛;
方案二:第一轮比赛种子选手与种子选手比赛.
您最近一年使用:0次