解题方法
1 . 已知定义域为 的奇函数
的奇函数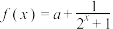 .
.
(1)求a;
(2)若 ,求t的取值范围.
,求t的取值范围.
 的奇函数
的奇函数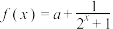 .
.(1)求a;
(2)若
 ,求t的取值范围.
,求t的取值范围.
您最近一年使用:0次
名校
2 . 已知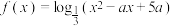 .
.
(1)若 ,求
,求 的值域;
的值域;
(2)若 在
在 上单调递减,求a的取值范围.
上单调递减,求a的取值范围.
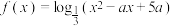 .
.(1)若
 ,求
,求 的值域;
的值域;(2)若
 在
在 上单调递减,求a的取值范围.
上单调递减,求a的取值范围.
您最近一年使用:0次
2023-10-10更新
|
1375次组卷
|
3卷引用:山东省泰安市宁阳县第四中学2023-2024学年高三上学期10月月考数学试题
山东省泰安市宁阳县第四中学2023-2024学年高三上学期10月月考数学试题山东省泰安市宁阳县2023-2024学年高三上学期第一次阶段性测试数学试题(已下线)模块一 专题1 对数与对数函数(人教A)2
名校
解题方法
3 . 已知函数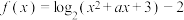 .
.
(1)若 ,求函数
,求函数 的值域
的值域
(2)若函数 在
在 上单调递增,求
上单调递增,求 的取值范围
的取值范围
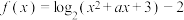 .
.(1)若
 ,求函数
,求函数 的值域
的值域(2)若函数
 在
在 上单调递增,求
上单调递增,求 的取值范围
的取值范围
您最近一年使用:0次
2023-09-21更新
|
1554次组卷
|
11卷引用:安徽省淮北市实验高级中学2022-2023学年高一上学期期末数学试题
安徽省淮北市实验高级中学2022-2023学年高一上学期期末数学试题(已下线)专题4.4 对数函数【八大题型】-举一反三系列(已下线)专题4.6 指、对数函数的综合应用大题专项训练-举一反三系列(已下线)4.4 对数函数(重难点突破)-【冲刺满分】(已下线)第四章 幂函数、指数函数与对数函数(知识归纳+题型突破)-速记·巧练(沪教版2020必修第一册)(已下线)4.3 对数函数-同步精品课堂(沪教版2020必修第一册)(已下线)模块四专题4 大题分类练(对数函数及其应用)拔高提升练(人教A)(已下线)模块一 专题1 对数与对数函数(人教A)2(已下线)第四章 指数函数与对数函数单元测试(基础版)-【冲刺满分】(已下线)6.3 对数函数(3)-【帮课堂】(苏教版2019必修第一册)(已下线)高一上学期期末复习【第四章 指数函数与对数函数】十大题型归纳(基础篇)-举一反三系列
解题方法
4 . 已知函数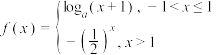 ,(
,( 且
且 )的最小值为
)的最小值为 .
.
(1)求 的值;
的值;
(2)设函数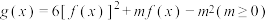 ,求
,求 零点个数.
零点个数.
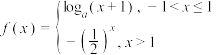 ,(
,( 且
且 )的最小值为
)的最小值为 .
.(1)求
 的值;
的值;(2)设函数
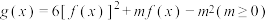 ,求
,求 零点个数.
零点个数.
您最近一年使用:0次
解题方法
5 . 已知函数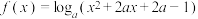 .
.
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)若 在
在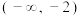 上单调递减,求a的取值范围.
上单调递减,求a的取值范围.
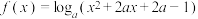 .
.(1)当
 时,求函数
时,求函数 的单调区间;
的单调区间;(2)若
 在
在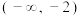 上单调递减,求a的取值范围.
上单调递减,求a的取值范围.
您最近一年使用:0次
名校
解题方法
6 . 已知函数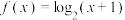 ,
,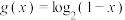 .
.
(1)求函数 的定义域;
的定义域;
(2)若不等式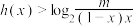 在
在 上恒成立,求实数
上恒成立,求实数 取值范围.
取值范围.
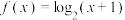 ,
,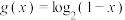 .
.(1)求函数
 的定义域;
的定义域;(2)若不等式
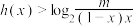 在
在 上恒成立,求实数
上恒成立,求实数 取值范围.
取值范围.
您最近一年使用:0次
名校
解题方法
7 . 已知函数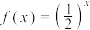 ,函数
,函数 图象与
图象与 的图象关于
的图象关于 对称.
对称.
(1)若函数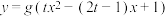 在
在 上单调递减,求实数
上单调递减,求实数 的取值范围;
的取值范围;
(2)不等式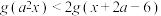 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
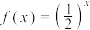 ,函数
,函数 图象与
图象与 的图象关于
的图象关于 对称.
对称.(1)若函数
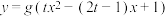 在
在 上单调递减,求实数
上单调递减,求实数 的取值范围;
的取值范围;(2)不等式
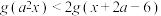 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-02-15更新
|
697次组卷
|
3卷引用:湖北省黄冈市2022-2023学年高一上学期元月期末数学试题
名校
解题方法
8 . 已知函数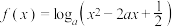 (
( 且
且 ).
).
(1)若 ,求
,求 的值域;
的值域;
(2)若 ,
, 在
在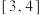 上单调递增,求
上单调递增,求 的取值范围.
的取值范围.
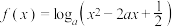 (
( 且
且 ).
).(1)若
 ,求
,求 的值域;
的值域;(2)若
 ,
, 在
在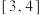 上单调递增,求
上单调递增,求 的取值范围.
的取值范围.
您最近一年使用:0次
2023-02-12更新
|
395次组卷
|
2卷引用:广东省深圳市人大附中深圳学校2022-2023学年高一上学期期末数学试题
名校
9 . 已知函数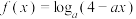 .
.
(1)若当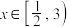 时,函数
时,函数 有意义,求实数
有意义,求实数 的取值范围.
的取值范围.
(2)是否存在实数 ,使得函数
,使得函数 在
在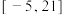 上为增函数,并且在此区间的最小值为
上为增函数,并且在此区间的最小值为 ?若存在,试求出
?若存在,试求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
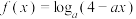 .
.(1)若当
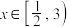 时,函数
时,函数 有意义,求实数
有意义,求实数 的取值范围.
的取值范围.(2)是否存在实数
 ,使得函数
,使得函数 在
在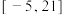 上为增函数,并且在此区间的最小值为
上为增函数,并且在此区间的最小值为 ?若存在,试求出
?若存在,试求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
2023-02-10更新
|
282次组卷
|
3卷引用:河南省信阳市2022-2023学年高一下学期阶段性测试(开学考)数学试题
10 . 已知函数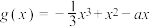 在
在 上单调递减,设实数a的取值集合为M.
上单调递减,设实数a的取值集合为M.
(1)求 ;
;
(2)若函数 在区间M上单调递增,求实数m的取值范围.
在区间M上单调递增,求实数m的取值范围.
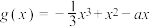 在
在 上单调递减,设实数a的取值集合为M.
上单调递减,设实数a的取值集合为M.(1)求
 ;
;(2)若函数
 在区间M上单调递增,求实数m的取值范围.
在区间M上单调递增,求实数m的取值范围.
您最近一年使用:0次



