1 . 若数列 和
和 的项数均为
的项数均为 ,则将数列
,则将数列 和
和 的距离定义为
的距离定义为 .
.
(1)求数列1,3,5,6和数列2,3,10,7的距离;
(2)记A为满足递推关系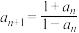 的所有数列
的所有数列 的集合,数列
的集合,数列 和
和 为A中的两个元素,且项数均为
为A中的两个元素,且项数均为 .若
.若 ,
, ,数列
,数列 和
和 的距离
的距离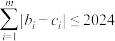 ,求m的最大值;
,求m的最大值;
(3)记S是所有7项数列 (其中
(其中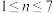 ,
, 或1)的集合,
或1)的集合,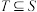 ,且T中的任何两个元素的距离大于或等于3.求证:T中的元素个数小于或等于16.
,且T中的任何两个元素的距离大于或等于3.求证:T中的元素个数小于或等于16.
 和
和 的项数均为
的项数均为 ,则将数列
,则将数列 和
和 的距离定义为
的距离定义为 .
.(1)求数列1,3,5,6和数列2,3,10,7的距离;
(2)记A为满足递推关系
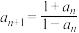 的所有数列
的所有数列 的集合,数列
的集合,数列 和
和 为A中的两个元素,且项数均为
为A中的两个元素,且项数均为 .若
.若 ,
, ,数列
,数列 和
和 的距离
的距离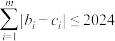 ,求m的最大值;
,求m的最大值;(3)记S是所有7项数列
 (其中
(其中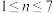 ,
, 或1)的集合,
或1)的集合,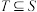 ,且T中的任何两个元素的距离大于或等于3.求证:T中的元素个数小于或等于16.
,且T中的任何两个元素的距离大于或等于3.求证:T中的元素个数小于或等于16.
您最近一年使用:0次
2 . 变分法是研究变元函数达到极值的必要条件和充要条件,欧拉、拉格朗日等数学家为其奠定了理论基础,其中“平缓函数”是变分法中的一个重要概念.设 是定义域为
是定义域为 的函数,如果对任意的
的函数,如果对任意的 均成立,则称
均成立,则称 是“平缓函数”.
是“平缓函数”.
(1)若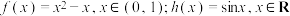 .试判断
.试判断 和
和 是否为“平缓函数”?并说明理由;(参考公式:①
是否为“平缓函数”?并说明理由;(参考公式:① 时,
时,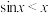 恒成立;②
恒成立;②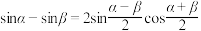 .)
.)
(2)若函数 是周期为2的“平缓函数”,证明:对定义域内任意的
是周期为2的“平缓函数”,证明:对定义域内任意的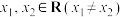 ,均有
,均有 ;
;
(3)设 为定义在
为定义在 上的函数,且存在正常数
上的函数,且存在正常数 ,使得函数
,使得函数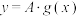 为“平缓函数”.现定义数列
为“平缓函数”.现定义数列 满足:
满足: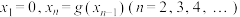 ,试证明:对任意的正整数
,试证明:对任意的正整数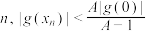 .
.
(参考公式: 且
且 时,
时,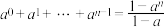 .)
.)
 是定义域为
是定义域为 的函数,如果对任意的
的函数,如果对任意的 均成立,则称
均成立,则称 是“平缓函数”.
是“平缓函数”.(1)若
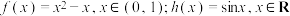 .试判断
.试判断 和
和 是否为“平缓函数”?并说明理由;(参考公式:①
是否为“平缓函数”?并说明理由;(参考公式:① 时,
时,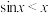 恒成立;②
恒成立;②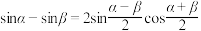 .)
.)(2)若函数
 是周期为2的“平缓函数”,证明:对定义域内任意的
是周期为2的“平缓函数”,证明:对定义域内任意的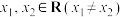 ,均有
,均有 ;
;(3)设
 为定义在
为定义在 上的函数,且存在正常数
上的函数,且存在正常数 ,使得函数
,使得函数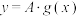 为“平缓函数”.现定义数列
为“平缓函数”.现定义数列 满足:
满足: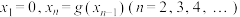 ,试证明:对任意的正整数
,试证明:对任意的正整数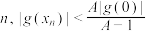 .
.(参考公式:
 且
且 时,
时,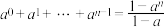 .)
.)
您最近一年使用:0次
2024-04-26更新
|
387次组卷
|
3卷引用:云南省昆明市云南师范大学附属中学2023-2024学年高一下学期教学测评期中卷数学试卷
云南省昆明市云南师范大学附属中学2023-2024学年高一下学期教学测评期中卷数学试卷四川省成都市成飞中学2023-2024学年高一下学期5月月考数学试题(已下线)专题10 利用微分中值法证明不等式【讲】
3 . 已知数列 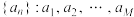 , 数列
, 数列 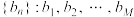 , 其中
, 其中  , 且
, 且 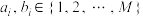 ,
, 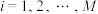 . 记
. 记 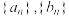 的前
的前  项和分别为
项和分别为 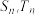 , 规定
, 规定  .记
.记 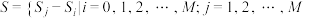 ,且
,且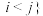 ,
, , 且
, 且 
(1)若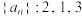 ,
,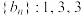 ,写出
,写出  ;
;
(2)若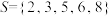 ,写出所有满足条件的数列
,写出所有满足条件的数列  , 并说明理由;
, 并说明理由;
(3)若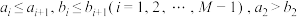 , 且
, 且  . 证明:
. 证明:  , 使得
, 使得  .
.
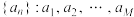 , 数列
, 数列 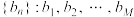 , 其中
, 其中  , 且
, 且 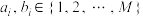 ,
, 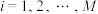 . 记
. 记 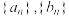 的前
的前  项和分别为
项和分别为 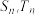 , 规定
, 规定  .记
.记 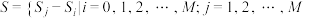 ,且
,且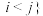 ,
, , 且
, 且 
(1)若
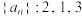 ,
,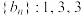 ,写出
,写出  ;
;(2)若
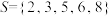 ,写出所有满足条件的数列
,写出所有满足条件的数列  , 并说明理由;
, 并说明理由;(3)若
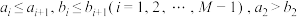 , 且
, 且  . 证明:
. 证明:  , 使得
, 使得  .
.
您最近一年使用:0次
4 . 差分法的定义:若数列 的前
的前 项和为
项和为 ,且
,且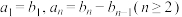 ,则
,则 时,
时,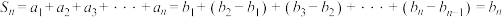 .例如:已知数列
.例如:已知数列 的通项公式是
的通项公式是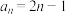 ,前
,前 项和为
项和为 ,因为
,因为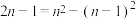 ,所以
,所以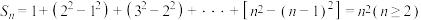 .
.
(1)若数列 的通项公式是
的通项公式是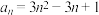 ,求
,求 的前
的前 项和
项和 ;
;
(2)若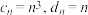 ,且数列
,且数列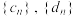 的前
的前 项和分别为
项和分别为 ,证明:
,证明: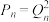 .
.
 的前
的前 项和为
项和为 ,且
,且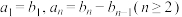 ,则
,则 时,
时,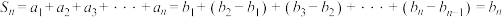 .例如:已知数列
.例如:已知数列 的通项公式是
的通项公式是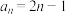 ,前
,前 项和为
项和为 ,因为
,因为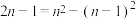 ,所以
,所以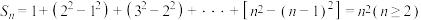 .
.(1)若数列
 的通项公式是
的通项公式是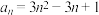 ,求
,求 的前
的前 项和
项和 ;
;(2)若
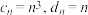 ,且数列
,且数列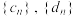 的前
的前 项和分别为
项和分别为 ,证明:
,证明: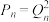 .
.
您最近一年使用:0次
2024-05-30更新
|
163次组卷
|
2卷引用:黑龙江省伊春市铁力市第一中学校2023-2024学年高二下学期期中考试数学试卷
5 . 对于数列 ,
, ,…,
,…,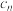 ,记
,记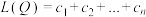 ,
,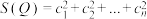 .设数列
.设数列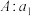 ,
, ,…,
,…, 和数列
和数列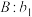 ,
, ,…,
,…, 是两个递增数列,若A与
是两个递增数列,若A与 满足
满足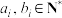 ,
,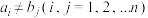 ,且
,且 ,
, ,则称A,
,则称A, 具有
具有 关系.
关系.
(1)若数列A:4,7,13和数列 :3,
:3, ,
, 具有
具有 关系,求
关系,求 ,
, 的值;
的值;
(2)证明:当 时,存在无数对具有
时,存在无数对具有 关系的数列;
关系的数列;
(3)当 时,直接写出一对具有
时,直接写出一对具有 关系的数列
关系的数列 和
和 .(本小问不用写解答过程)
.(本小问不用写解答过程)
 ,
, ,…,
,…,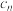 ,记
,记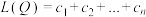 ,
,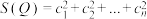 .设数列
.设数列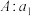 ,
, ,…,
,…, 和数列
和数列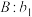 ,
, ,…,
,…, 是两个递增数列,若A与
是两个递增数列,若A与 满足
满足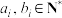 ,
,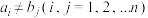 ,且
,且 ,
, ,则称A,
,则称A, 具有
具有 关系.
关系.(1)若数列A:4,7,13和数列
 :3,
:3, ,
, 具有
具有 关系,求
关系,求 ,
, 的值;
的值;(2)证明:当
 时,存在无数对具有
时,存在无数对具有 关系的数列;
关系的数列;(3)当
 时,直接写出一对具有
时,直接写出一对具有 关系的数列
关系的数列 和
和 .(本小问不用写解答过程)
.(本小问不用写解答过程)
您最近一年使用:0次
6 . 已知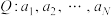 为有穷正整数数列,
为有穷正整数数列,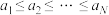 ,且
,且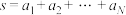 .从
.从 中选取第
中选取第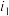 项,第
项,第 项,
项, ,第
,第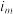 项
项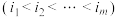 ,称数列
,称数列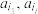 ,
,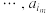 为
为 的长度为
的长度为 的子列.规定:数列
的子列.规定:数列 的任意一项都是
的任意一项都是 的长度为1的子列.若对于任意的正整数
的长度为1的子列.若对于任意的正整数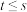 ,数列
,数列 存在长度为
存在长度为 的子列
的子列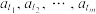 ,使得
,使得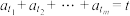 ,则称数列
,则称数列 为全覆盖数列.
为全覆盖数列.
(1)判断数列 和数列
和数列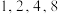 是否为全覆盖数列;
是否为全覆盖数列;
(2)在数列 中,若
中,若 ,求证:当
,求证:当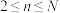 时,
时, ;
;
(3)若数列 满足:
满足: ,且当
,且当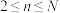 时,
时,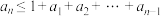 ,求证:数列
,求证:数列 为全覆盖数列.
为全覆盖数列.
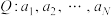 为有穷正整数数列,
为有穷正整数数列,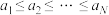 ,且
,且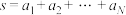 .从
.从 中选取第
中选取第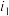 项,第
项,第 项,
项, ,第
,第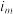 项
项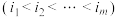 ,称数列
,称数列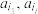 ,
,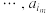 为
为 的长度为
的长度为 的子列.规定:数列
的子列.规定:数列 的任意一项都是
的任意一项都是 的长度为1的子列.若对于任意的正整数
的长度为1的子列.若对于任意的正整数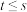 ,数列
,数列 存在长度为
存在长度为 的子列
的子列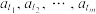 ,使得
,使得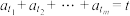 ,则称数列
,则称数列 为全覆盖数列.
为全覆盖数列.(1)判断数列
 和数列
和数列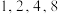 是否为全覆盖数列;
是否为全覆盖数列;(2)在数列
 中,若
中,若 ,求证:当
,求证:当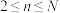 时,
时, ;
;(3)若数列
 满足:
满足: ,且当
,且当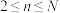 时,
时,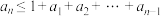 ,求证:数列
,求证:数列 为全覆盖数列.
为全覆盖数列.
您最近一年使用:0次
名校
解题方法
7 . 若给定数列 ,对于任意的
,对于任意的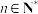 ,若满足
,若满足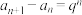 ,则称
,则称 为“
为“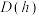 型数列”.若数列
型数列”.若数列 满足:
满足: ,
,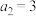 ,当
,当 时,
时,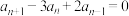 .
.
(1)判断数列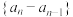 是否为“
是否为“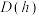 型数列”,并证明;
型数列”,并证明;
(2)求数列 的通项公式;
的通项公式;
(3)若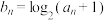 ,
,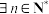 ,使不等式
,使不等式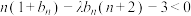 成立,求实数
成立,求实数 的取值范围.
的取值范围.
 ,对于任意的
,对于任意的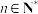 ,若满足
,若满足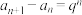 ,则称
,则称 为“
为“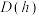 型数列”.若数列
型数列”.若数列 满足:
满足: ,
,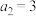 ,当
,当 时,
时,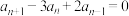 .
.(1)判断数列
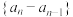 是否为“
是否为“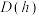 型数列”,并证明;
型数列”,并证明;(2)求数列
 的通项公式;
的通项公式;(3)若
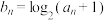 ,
,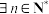 ,使不等式
,使不等式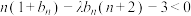 成立,求实数
成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
8 . 已知 为有穷整数数列,若
为有穷整数数列,若 满足:
满足: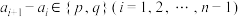 ,其中
,其中 ,
, 是两个给定的不同非零整数,且
是两个给定的不同非零整数,且 ,则称
,则称 具有性质
具有性质 .
.
(1)若 ,
, ,那么是否存在具有性质
,那么是否存在具有性质 的
的 ?若存在,写出一个这样的
?若存在,写出一个这样的 ;若不存在,请说明理由;
;若不存在,请说明理由;
(2)若 ,
, ,且
,且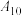 具有性质
具有性质 ,求证:
,求证: 中必有两项相同;
中必有两项相同;
(3)若 ,求证:存在正整数
,求证:存在正整数 ,使得对任意具有性质
,使得对任意具有性质 的
的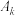 ,都有
,都有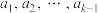 中任意两项均不相同.
中任意两项均不相同.
 为有穷整数数列,若
为有穷整数数列,若 满足:
满足: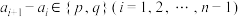 ,其中
,其中 ,
, 是两个给定的不同非零整数,且
是两个给定的不同非零整数,且 ,则称
,则称 具有性质
具有性质 .
.(1)若
 ,
, ,那么是否存在具有性质
,那么是否存在具有性质 的
的 ?若存在,写出一个这样的
?若存在,写出一个这样的 ;若不存在,请说明理由;
;若不存在,请说明理由;(2)若
 ,
, ,且
,且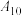 具有性质
具有性质 ,求证:
,求证: 中必有两项相同;
中必有两项相同;(3)若
 ,求证:存在正整数
,求证:存在正整数 ,使得对任意具有性质
,使得对任意具有性质 的
的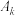 ,都有
,都有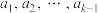 中任意两项均不相同.
中任意两项均不相同.
您最近一年使用:0次
解题方法
9 . 将数列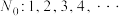 中项数为平方数的项依次选出构成数列
中项数为平方数的项依次选出构成数列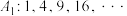 ,此时数列
,此时数列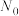 中剩下的项构成数列
中剩下的项构成数列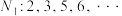 ;再将数列
;再将数列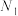 中项数为平方数的项依次选出构成数列
中项数为平方数的项依次选出构成数列 ,剩下的项构成数列
,剩下的项构成数列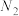 ;….如此操作下去,将数列
;….如此操作下去,将数列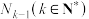 中项数为平方数的项依次选出构成数列
中项数为平方数的项依次选出构成数列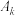 ,剩下的项构成数列
,剩下的项构成数列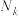 .
.
(1)分别写出数列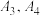 的前2项;
的前2项;
(2)记数列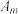 的第
的第 项为
项为 .求证:当
.求证:当 时,
时, ;
;
(3)若 ,求
,求 的值.
的值.
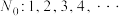 中项数为平方数的项依次选出构成数列
中项数为平方数的项依次选出构成数列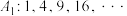 ,此时数列
,此时数列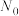 中剩下的项构成数列
中剩下的项构成数列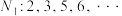 ;再将数列
;再将数列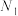 中项数为平方数的项依次选出构成数列
中项数为平方数的项依次选出构成数列 ,剩下的项构成数列
,剩下的项构成数列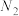 ;….如此操作下去,将数列
;….如此操作下去,将数列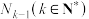 中项数为平方数的项依次选出构成数列
中项数为平方数的项依次选出构成数列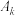 ,剩下的项构成数列
,剩下的项构成数列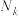 .
.(1)分别写出数列
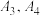 的前2项;
的前2项;(2)记数列
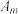 的第
的第 项为
项为 .求证:当
.求证:当 时,
时, ;
;(3)若
 ,求
,求 的值.
的值.
您最近一年使用:0次
名校
10 . 已知: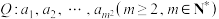 为有穷正整数数列,其最大项的值为
为有穷正整数数列,其最大项的值为 ,且当
,且当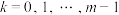 时,均有
时,均有 .设
.设 ,对于
,对于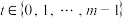 ,定义
,定义 ,其中,
,其中,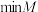 表示数集M中最小的数.
表示数集M中最小的数.
(1)若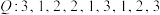 ,写出
,写出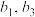 的值;
的值;
(2)若存在 满足:
满足: ,求
,求 的最小值;
的最小值;
(3)当 时,证明:对所有
时,证明:对所有 .
.
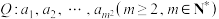 为有穷正整数数列,其最大项的值为
为有穷正整数数列,其最大项的值为 ,且当
,且当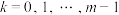 时,均有
时,均有 .设
.设 ,对于
,对于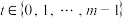 ,定义
,定义 ,其中,
,其中,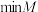 表示数集M中最小的数.
表示数集M中最小的数.(1)若
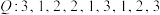 ,写出
,写出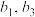 的值;
的值;(2)若存在
 满足:
满足: ,求
,求 的最小值;
的最小值;(3)当
 时,证明:对所有
时,证明:对所有 .
.
您最近一年使用:0次
2024-04-09更新
|
1110次组卷
|
4卷引用:北京市海淀区2024届高三下学期期中练习(一模)数学试题
北京市海淀区2024届高三下学期期中练习(一模)数学试题2024届河北省雄安新区部分高中高考三模数学试题甘肃省白银市靖远县第一中学2024届高三下学期模拟预测数学试题(已下线)2024年北京高考数学真题平行卷(提升)



