名校
解题方法
1 . 英国物理学家牛顿用“作切线”的方法求函数的零点时,给出的“牛顿数列”在航空航天中应用广泛,若数列 满足
满足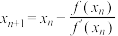 ,则称数列
,则称数列 为牛顿数列,如果
为牛顿数列,如果 ,数列
,数列 为牛顿数列,设
为牛顿数列,设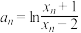 且
且 ,
, ,数列
,数列 的前
的前 项和为
项和为 ,则
,则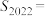 ( )
( )
 满足
满足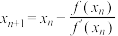 ,则称数列
,则称数列 为牛顿数列,如果
为牛顿数列,如果 ,数列
,数列 为牛顿数列,设
为牛顿数列,设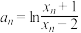 且
且 ,
, ,数列
,数列 的前
的前 项和为
项和为 ,则
,则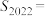 ( )
( )A. | B.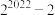 | C.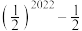 | D.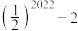 |
您最近一年使用:0次
2022-09-14更新
|
1560次组卷
|
9卷引用:宁夏银川一中2023届高三上学期第二次月考数学(文)试题
宁夏银川一中2023届高三上学期第二次月考数学(文)试题内蒙古赤峰市2021-2022年高三上学期第一次统一模拟考试文科数学试题(已下线)专题9 牛顿辽宁省锦州市2021-2022学年高二下学期期末考试数学试题(已下线)模块四 专题2 期末重组综合练(辽宁)(高二人教B)辽宁省沈阳市浑南区东北育才学校科学高中部2023-2024学年高三上学期高考适应性测试(一)数学试题安徽省2024届高三上学期8月摸底大联考数学试题(已下线)第十章 导数与数学文化 微点2 导数与数学文化(二)(已下线)拔高点突破01 新情景、新定义下的数列问题(七大题型)
2 . 记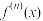 为函数
为函数 的
的 阶导数且
阶导数且 ,
, 若
若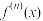 存在,则称
存在,则称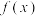
 阶可导.英国数学家泰勒发现:若
阶可导.英国数学家泰勒发现:若 在
在 附近
附近 阶可导,则可构造
阶可导,则可构造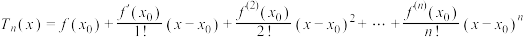 (称为
(称为 次泰勒多项式)来逼近
次泰勒多项式)来逼近 在
在 附近的函数值.据此计算
附近的函数值.据此计算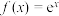 在
在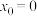 处的3次泰勒多项式为
处的3次泰勒多项式为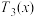 =
=_________ ; 在
在 处的10次泰勒多项式中
处的10次泰勒多项式中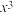 的系数为
的系数为_________
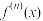 为函数
为函数 的
的 阶导数且
阶导数且 ,
, 若
若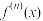 存在,则称
存在,则称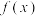
 阶可导.英国数学家泰勒发现:若
阶可导.英国数学家泰勒发现:若 在
在 附近
附近 阶可导,则可构造
阶可导,则可构造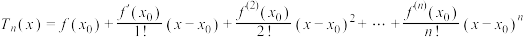 (称为
(称为 次泰勒多项式)来逼近
次泰勒多项式)来逼近 在
在 附近的函数值.据此计算
附近的函数值.据此计算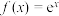 在
在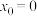 处的3次泰勒多项式为
处的3次泰勒多项式为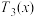 =
= 在
在 处的10次泰勒多项式中
处的10次泰勒多项式中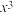 的系数为
的系数为
您最近一年使用:0次
2022-06-11更新
|
2064次组卷
|
4卷引用:广东省深圳市光明区高级中学等2022届高三下学期名校联考数学试题
广东省深圳市光明区高级中学等2022届高三下学期名校联考数学试题江苏省南京市宁海中学2022-2023学年高三下学期二月检测数学试题(已下线)专题6 “高数衔接”类型(已下线)第十章 导数与数学文化 微点2 导数与数学文化(二)
名校
解题方法
3 . 意大利画家列奥纳多·达・芬奇的画作《抱银鼠的女子》中,女士脖颈上黑色珍珠项链与主人相互映衬呈现出不一样的美与光泽,达・芬奇提出:固定项链的两端,使其在重力的作用下自然下垂,项链所形成的曲线是什么?这就是著名的“悬链线问题”.后人给出了悬链线的函数解析式: 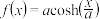 ,其中
,其中 为曲线顶点到横坐标轴的距离,
为曲线顶点到横坐标轴的距离, 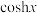 称为双曲余弦函数,其函数表达式为
称为双曲余弦函数,其函数表达式为 ,相应地,双曲正弦函数的表达式为
,相应地,双曲正弦函数的表达式为
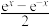 .若直线
.若直线 与双曲余弦函数
与双曲余弦函数 双曲正弦函数
双曲正弦函数 的图象分别相交于点
的图象分别相交于点 ,
, ,曲线
,曲线 在点
在点 处的切线
处的切线 与曲线
与曲线 在点
在点 处的切线
处的切线 相交于点
相交于点 ,则下列结论正确的为( )
,则下列结论正确的为( )
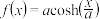 ,其中
,其中 为曲线顶点到横坐标轴的距离,
为曲线顶点到横坐标轴的距离, 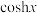 称为双曲余弦函数,其函数表达式为
称为双曲余弦函数,其函数表达式为 ,相应地,双曲正弦函数的表达式为
,相应地,双曲正弦函数的表达式为
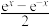 .若直线
.若直线 与双曲余弦函数
与双曲余弦函数 双曲正弦函数
双曲正弦函数 的图象分别相交于点
的图象分别相交于点 ,
, ,曲线
,曲线 在点
在点 处的切线
处的切线 与曲线
与曲线 在点
在点 处的切线
处的切线 相交于点
相交于点 ,则下列结论正确的为( )
,则下列结论正确的为( )A.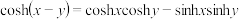 |
B. 是偶函数 是偶函数 |
C. |
D.若 是以 是以 为直角顶点的直角三角形,则实数 为直角顶点的直角三角形,则实数 |
您最近一年使用:0次
2022-04-10更新
|
1585次组卷
|
21卷引用:广东省佛山市南海一中2021-2022学年高二下学期第二次大测数学试题
广东省佛山市南海一中2021-2022学年高二下学期第二次大测数学试题湖北省八市2021届高三下学期3月联考数学试题湖南省长沙市长郡中学2021届高三下学期月考(七)数学试题重庆市第三十七中学校2020-2021学年高二下学期5月月考数学试题人教B版(2019) 选修第三册 名师精选 第七单元 基本初等函数的导数、求导法则及其应用(A卷)吉林省长春市第五中学2021-2022学年高二下学期期中数学试题云南省楚雄天人中学2022-2023学年高二下学期3月学习效果监测数学试题(已下线)河南省信阳高级中学2023-2024学年高三上学期8月月考数学试题广东省佛山市南海区桂城中学2023-2024学年高三下学期5月月考数学试题(已下线)仿真系列卷(04) - 决胜2021高考数学仿真系列卷(江苏等八省新高考地区专用)山东省(新高考)2021届高三 数学第二次模拟考试题(一)(已下线)2021年高考数学押题预测卷(新高考卷)01湖南省长沙市雅礼中学2021届高三下学期高考热身训练数学试题北师大版(2019) 选修第二册 名师精选 第七单元 导数的计算、导数的四则运算法则、简单复合函数的求导法则(A卷)(已下线)5.2导数的运算(A 基础培优练)-2021-2022学年高二数学同步双培优检测(苏教版2019选择性必修第一册)福建省福清西山学校2022届高三上学期期中考试数学试题(已下线)卷08 导数的概念及其意义、导数的运算·B卷·能力提升 -【重难点突破】2021-2022学年高二数学名校好题汇编同步测试卷(人教A版选择性必修第二册)(已下线)专题23数学文化与新情境问题(已下线)第十章 导数与数学文化 微点3 导数与数学文化(三)(已下线)模块四 专题1 高考新题型专练(新定义专练)(人教A)(高二)(已下线)模块三 专题3 高考新题型专练 专题2 新定义专练(苏教版)
4 . 拉格朗日中值定理是微分学中的基本定理之一,定理内容是:如果函数 在闭区间
在闭区间 上的图象连续不间断,在开区间
上的图象连续不间断,在开区间 内的导数为
内的导数为 ,那么在区间
,那么在区间 内至少存在一点c,使得
内至少存在一点c,使得 成立,其中c叫做
成立,其中c叫做 在
在 上的“拉格朗日中值点”.根据这个定理,可得函数
上的“拉格朗日中值点”.根据这个定理,可得函数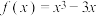 在
在 上的“拉格朗日中值点”的个数为( )
上的“拉格朗日中值点”的个数为( )
 在闭区间
在闭区间 上的图象连续不间断,在开区间
上的图象连续不间断,在开区间 内的导数为
内的导数为 ,那么在区间
,那么在区间 内至少存在一点c,使得
内至少存在一点c,使得 成立,其中c叫做
成立,其中c叫做 在
在 上的“拉格朗日中值点”.根据这个定理,可得函数
上的“拉格朗日中值点”.根据这个定理,可得函数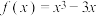 在
在 上的“拉格朗日中值点”的个数为( )
上的“拉格朗日中值点”的个数为( )| A.3 | B.2 | C.1 | D.0 |
您最近一年使用:0次
2022-03-21更新
|
1303次组卷
|
11卷引用:江苏省南通市如皋市2021-2022学年高二下学期第一次调研测试数学试题
(已下线)江苏省南通市如皋市2021-2022学年高二下学期第一次调研测试数学试题广东省深圳市南山区华侨城中学2021-2022学年高二下学期3月月考数学试题江苏省南通市石庄高级中学2021-2022学年高二下学期3月第一次调研数学试题广东省中山市迪茵公学2021-2022学年高二下学期第一次段考数学试题重庆市朝阳中学2021-2022学年高二下学期期中数学试题(已下线)专题23 拉格朗日安徽省合肥市肥东县综合高中2021-2022学年高二下学期期中考试数学(理)试题山东省菏泽市定陶区明德学校(山大附中实验学校)2022-2023学年高二下学期创新部第一次月考数学试题辽宁省沈阳市第三十六中学2022-2023学年高二下学期6月月考数学试题内蒙古赤峰二中2022-2023学年高二下学期第二次月考数学(理)试题江苏省盐城市五校联盟2023-2024学年高二上学期1月期末考试数学试题
名校
5 . 吹气球时,气球的体积 (单位:
(单位: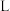 )与半径
)与半径 (单位:
(单位: )之间的关系是
)之间的关系是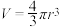 .当
.当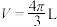 时,气球的瞬时膨胀率为( )
时,气球的瞬时膨胀率为( )
 (单位:
(单位: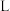 )与半径
)与半径 (单位:
(单位: )之间的关系是
)之间的关系是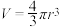 .当
.当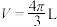 时,气球的瞬时膨胀率为( )
时,气球的瞬时膨胀率为( )A.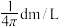 | B. | C.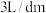 | D.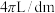 |
您最近一年使用:0次
2022-03-09更新
|
1166次组卷
|
6卷引用:河北省部分名校(唐县第一中学等)2022届高三下学期3月联考数学试题
6 . 十八世纪,数学家泰勒发现了公式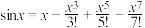
 …,其中
…,其中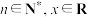 ,若
,若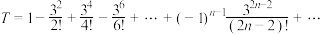 ,下列选项中与
,下列选项中与 的值最接近的是( )
的值最接近的是( )
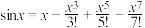
 …,其中
…,其中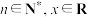 ,若
,若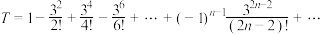 ,下列选项中与
,下列选项中与 的值最接近的是( )
的值最接近的是( )A. | B. | C.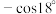 | D. |
您最近一年使用:0次
2022-01-23更新
|
1945次组卷
|
6卷引用:重庆市实验中学2021-2022学年高二下学期第一次月考数学试题
重庆市实验中学2021-2022学年高二下学期第一次月考数学试题山东省日照市校际联合考试2021-2022学年高三上学期期末数学试题(已下线)第5章 一元函数的导数及其应用(新文化与压轴30题专练)-2021-2022学年高二数学下学期考试满分全攻略(人教A版2019选修第二册+第三册)(已下线)专题13 泰勒(已下线)第十章 导数与数学文化 微点4 导数与数学文化综合训练(已下线)第19题 方程根与泰勒公式的估值艺术(高三备考9月刊)
名校
7 . 用数学的眼光看世界就能发现很多数学之“美”.现代建筑讲究线条感,曲线之美让人称奇.衡量曲线弯曲程度的重要指标是曲率,曲线的曲率定义如下:若 是
是 的导函数,
的导函数, 是
是 的导函数,则曲线
的导函数,则曲线 在点
在点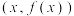 处的曲率
处的曲率 .若曲线
.若曲线 与
与 在
在 处的曲率分别为
处的曲率分别为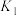 ,
,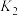 ,
,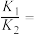 ( )
( )
 是
是 的导函数,
的导函数, 是
是 的导函数,则曲线
的导函数,则曲线 在点
在点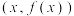 处的曲率
处的曲率 .若曲线
.若曲线 与
与 在
在 处的曲率分别为
处的曲率分别为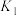 ,
,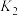 ,
,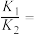 ( )
( )A. | B. | C.4 | D.2 |
您最近一年使用:0次
2021-09-01更新
|
1033次组卷
|
8卷引用:江苏省无锡市江阴高级中学2021-2022学年高二下学期3月月考数学试题
江苏省无锡市江阴高级中学2021-2022学年高二下学期3月月考数学试题吉林省延边第二中学2020-2021学年高二下学期期末考试数学(理)试题(已下线)数学与美术(已下线)高考新题型-一元函数的导数及其应用湖南省部分学校2022-2023学年高二下学期期中模拟数学试题(已下线)第五篇 向量与几何 专题21 曲率与曲率圆 微点2 曲率与曲率圆(二)(已下线)第十章 导数与数学文化 微点3 导数与数学文化(三)(已下线)核心考点2 导数几何意义和函数的单调性、极值 专题讲解 B提升卷 (高二期末考试必考的10大核心考点)
20-21高三下·全国·阶段练习
名校
解题方法
8 . 拉格朗日中值定理又称拉氏定理,是微积分学中的基本定理之一,它反映了函数在闭区间上的整体平均变化率与区间某点的局部变化率的关系,其具体内容如下:若 在
在 上满足以下条件:①在
上满足以下条件:①在 上图象连续,②在
上图象连续,②在 内导数存在,则在
内导数存在,则在 内至少存在一点
内至少存在一点 ,使得
,使得 (
( 为
为 的导函数).则函数
的导函数).则函数 在
在 上这样的
上这样的 点的个数为( )
点的个数为( )
 在
在 上满足以下条件:①在
上满足以下条件:①在 上图象连续,②在
上图象连续,②在 内导数存在,则在
内导数存在,则在 内至少存在一点
内至少存在一点 ,使得
,使得 (
( 为
为 的导函数).则函数
的导函数).则函数 在
在 上这样的
上这样的 点的个数为( )
点的个数为( )| A.1 | B.2 | C.3 | D.4 |
您最近一年使用:0次
2021-02-26更新
|
1594次组卷
|
15卷引用:安徽省亳州市蒙城第一中学东校区2022-2023学年高三上学期第四次月考数学试题
安徽省亳州市蒙城第一中学东校区2022-2023学年高三上学期第四次月考数学试题(已下线)天一大联考2021届高三下学期阶段检测(四)理科数学试题江西省吉安市遂川中学2021届高三下学期阶段性测试(四)数学(文)试题(已下线)天一大联考2021届高三下学期阶段检测(四)文科数学试题河南省十所名校2020-2021学年高中毕业班阶段性测试数学理科(四)试题江西省吉安市遂川中学2021届高三下学期阶段性测试(四)数学(理)试题(已下线)考向14 导数的概念及应用(重点)-备战2022年高考数学一轮复习考点微专题(新高考地区专用)(已下线)专题23 拉格朗日福建省福州第八中学2023届高三上学期半期适应性训练数学试题河南省洛阳市洛宁县第一高级中学2022-2023学年高二下学期2月月考数学理科试题河南省十所名校2020-2021学年高中毕业班阶段性测试数学文科(四)试题陕西省延安市子长市中学2020-2021学年高二下学期期中理科数学试题陕西省咸阳市泾阳县2020-2021学年高二下学期期中理科数学试题(已下线)第十章 导数与数学文化 微点2 导数与数学文化(二)(已下线)模块三 大招1 拉格朗日中值定理



