名校
解题方法
1 . 设正项等比数列 的前n项和为
的前n项和为 ,若
,若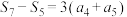 ,则
,则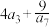 的最小值为( )
的最小值为( )
 的前n项和为
的前n项和为 ,若
,若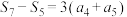 ,则
,则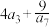 的最小值为( )
的最小值为( )| A.2 | B.4 | C.8 | D.16 |
您最近一年使用:0次
2023-02-26更新
|
1008次组卷
|
6卷引用:辽宁省铁岭市清河高级中学2022-2023学年高二下学期3月月考数学试题
辽宁省铁岭市清河高级中学2022-2023学年高二下学期3月月考数学试题辽宁省沈阳市第四十中学2022-2023学年高二下学期4月月考数学试题福建福州铜盘中学2022-2023学年高二上学期期末考试数学试题1.3等比数列 测试卷(已下线)期末真题必刷基础60题(31个考点专练)【满分全攻略】2023-2024学年高二数学同步讲义全优学案(人教A版2019选择性必修第一、二册)河南省南阳市第十中学校2023-2024学年高二下学期第一次月考数学试卷
2 . 已知数列 满足
满足 ,
,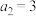 ,数列
,数列 为等比数列且公比
为等比数列且公比 ,满足
,满足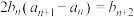 .
.
(1)求数列 的通项公式;
的通项公式;
(2)数列 的前n项和为
的前n项和为 ,若________,记数列
,若________,记数列 满足
满足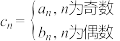 ,求数列
,求数列 的前
的前 项和
项和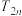 .
.
在①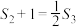 ,②
,② ,
,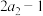 ,
, 成等差数列,③
成等差数列,③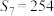 这三个条件中任选一个补充在第(2)问中,并对其求解.
这三个条件中任选一个补充在第(2)问中,并对其求解.
注:若选择多个条件分别解答,按第一个解答计分.
 满足
满足 ,
,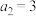 ,数列
,数列 为等比数列且公比
为等比数列且公比 ,满足
,满足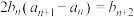 .
.(1)求数列
 的通项公式;
的通项公式;(2)数列
 的前n项和为
的前n项和为 ,若________,记数列
,若________,记数列 满足
满足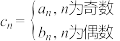 ,求数列
,求数列 的前
的前 项和
项和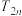 .
.在①
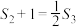 ,②
,② ,
,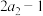 ,
, 成等差数列,③
成等差数列,③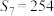 这三个条件中任选一个补充在第(2)问中,并对其求解.
这三个条件中任选一个补充在第(2)问中,并对其求解.注:若选择多个条件分别解答,按第一个解答计分.
您最近一年使用:0次
2023-02-24更新
|
615次组卷
|
4卷引用:辽宁省葫芦岛市2022-2023学年高三上学期期末数学试题
名校
3 . 已知等比数列 的公比为
的公比为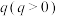 ,前
,前 项积为
项积为 ,若
,若 ,则( )
,则( )
 的公比为
的公比为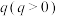 ,前
,前 项积为
项积为 ,若
,若 ,则( )
,则( )A. | B. |
C.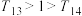 | D.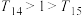 |
您最近一年使用:0次
2023-02-23更新
|
3518次组卷
|
17卷引用:辽宁省沈阳市东北育才学校2024届高三第三次模拟考试数学试题
辽宁省沈阳市东北育才学校2024届高三第三次模拟考试数学试题安徽省亳州市蒙城第一中学2023届高三下学期开学考试数学试题山西省三重教育2023届高三下学期2月联考数学试题河北省石家庄市十五中2022-2023学年高二下学期第二次月考数学试题浙江省杭州市余杭高级中学等四校2022-2023学年高二下学期3月联考数学试题河北省石家庄部分重点高中2023届高三下学期3月月考数学试题山西省朔州市怀仁市第一中学校2023届高三下学期2月月考数学试题广东省佛山市南海区2022-2023学年高二下学期期中数学试题江西省上高二中2024届高三第三次月考(10月)数学试题(已下线)河南省信阳市信阳高级中学2024届高三一模数学试题福建省莆田市第四中学2024届高三上学期第三次月考数学试题河南省许昌市禹州市高级中学2024届高三上学期12月月考数学试题湖南省长沙市长郡中学2024届高三上学期月考数学试题(五)(已下线)专题05 等比数列与数列综合求和-2023-2024学年高二数学期末复习重难培优与单元检测(人教A版2019)(已下线)专题04 数列(4)安徽省阜阳市第三中学2023-2024学年高二上学期期末数学试题河南省信阳高级中学2024届高三上学期月考(五)数学试题
4 . 已知 是等差数列,
是等差数列, 是等比数列,且
是等比数列,且 ,
, ,
, ,
, .
.
(1)求 的通项公式;
的通项公式;
(2)设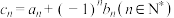 ,求数列
,求数列 的前2n项和.
的前2n项和.
 是等差数列,
是等差数列, 是等比数列,且
是等比数列,且 ,
, ,
, ,
, .
.(1)求
 的通项公式;
的通项公式;(2)设
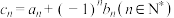 ,求数列
,求数列 的前2n项和.
的前2n项和.
您最近一年使用:0次
2023-02-21更新
|
3137次组卷
|
9卷引用:辽宁省沈阳市东北育才学校高中部2023-2024学年高三第六次模拟考试暨假期质量测试数学试题
辽宁省沈阳市东北育才学校高中部2023-2024学年高三第六次模拟考试暨假期质量测试数学试题上海市黄浦区2023届高三上学期一模数学试题江西省鹰潭市贵溪市第一中学2022-2023学年高二下学期3月第二次月考数学试题宁夏石嘴山市第三中学2023届高三第一次模拟考试数学(理)试题黑龙江省齐齐哈尔市第八中学校2022-2023学年高二下学期4月月考数学试题上海市建平中学2022-2023学年高一下学期期末数学试题上海市川沙中学2023-2024学年高一下学期数学5月月考数学试卷上海市复兴高级中学2023-2024学年高一下学期期末考试数学试卷【典例题】 4.2. 2.1 等比数列的前n项和 课堂例题-沪教版(2020)选择性必修第一册第4章 数列
5 . 设正项等比数列 的前n项和为
的前n项和为 ,且
,且 .
.
(1)求 的通项公式;
的通项公式;
(2)记 的前n项积为
的前n项积为 ,求使得
,求使得 取得最大值的n的值.
取得最大值的n的值.
 的前n项和为
的前n项和为 ,且
,且 .
.(1)求
 的通项公式;
的通项公式;(2)记
 的前n项积为
的前n项积为 ,求使得
,求使得 取得最大值的n的值.
取得最大值的n的值.
您最近一年使用:0次
名校
6 . 在等比数列 中
中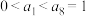 .则能使不等式
.则能使不等式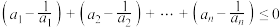 成立的正整数
成立的正整数 的最大值为( )
的最大值为( )
 中
中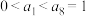 .则能使不等式
.则能使不等式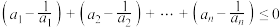 成立的正整数
成立的正整数 的最大值为( )
的最大值为( )| A.13 | B.14 | C.15 | D.16 |
您最近一年使用:0次
2023-01-18更新
|
832次组卷
|
10卷引用:辽宁省2022-2023学年高三上学期期末联考数学试题
辽宁省2022-2023学年高三上学期期末联考数学试题辽宁省朝阳市2023届高三上学期期末数学试题河南省南阳市第一中学校2022-2023学年高二下学期第一次月考数学试题青海省玉树州2023届高三第三次联考数学文科试题(已下线)专题6-1 数列函数性质与不等式放缩(讲+练)-2河南省实验中学2023届高三模拟考试四文科数学试题河南省南阳市方城县光明学校2022-2023学年高二下学期3月月考数学试题广东省佛山市顺德区华侨中学2024届高三港澳班上学期期中数学试题文科数学-【名校面对面】河南省三甲名校2023届高三校内模拟试题(四)(已下线)4.3.1等比数列的概念(第2课时)(分层作业)(4种题型)-【上好课】高二数学同步备课系列(人教A版2019选择性必修第二册)
7 . 在等比数列 中
中
(1)求 的通项公式;
的通项公式;
(2)设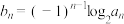 ,求
,求 的前n项和
的前n项和 .
.
 中
中
(1)求
 的通项公式;
的通项公式;(2)设
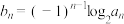 ,求
,求 的前n项和
的前n项和 .
.
您最近一年使用:0次
2023-01-18更新
|
712次组卷
|
4卷引用:辽宁省2022-2023学年高三上学期期末联考数学试题
名校
8 . 在等比数列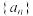 中,
中, ,
,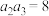 ,则
,则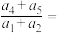 ( )
( )
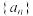 中,
中, ,
,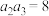 ,则
,则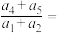 ( )
( )| A.8 | B.6 | C.4 | D.2 |
您最近一年使用:0次
2023-10-06更新
|
689次组卷
|
19卷引用:辽宁省沈阳市翔宇中学2021-2022高三上学期第二次月考数学试题
辽宁省沈阳市翔宇中学2021-2022高三上学期第二次月考数学试题河南省洛阳市2021-2022学年高三上学期期中理科数学试题河南省洛阳市2021-2022学年高三上学期期中文科数学试题(已下线)4.3.2等比数列通项公式(备作业)-【上好课】2021-2022学年高二数学同步备课系列(苏教版2019选择性必修第一册)(已下线)专题4.2 数列 章末检测2(中)-【满分计划】2021-2022学年高二数学阶段性复习测试卷(苏教版2019选择性必修第一册)(已下线)专题7.2 期末押题检测卷(考试范围:选择性必修第一册)2(中)-【满分计划】2021-2022学年高二数学阶段性复习测试卷(苏教版2019选择性必修第一册)(已下线)第17节 等比数列及前n项和(已下线)第19节 数列求和2023版 湘教版(2019) 选修第一册 过关斩将 第1章 1.3.1等比数列及其通项公式+1.3.2等比数列与指数函数(已下线)专题07 数列(测)福建省连城县第一中学2022-2023学年高二上学期第一次月考数学试题宁夏银川唐徕回民中学2022-2023学年高二上学期期中考试数学试题甘肃省兰州市第六十一中学2022-2023学年高二上学期期末数学试题福建省连城县第一中学2023-2024学年高二上学期10月月考数学试题甘肃省武威市民勤县第一中学2023-2024学年高二上学期第二次月考数学试题(已下线)4.3等比数列(1)(已下线)第4章 数列 章末题型归纳总结(1)(已下线)专题4.3 等比数列(5个考点八大题型)(1)(已下线)4.3.1 等比数列的概念——课后作业(提升版)
名校
解题方法
9 . 已知等差数列 的前n项的和为
的前n项的和为 ,
,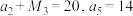 .数列
.数列 的前n项和为
的前n项和为 ,
,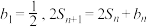 .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)若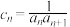 ,数列
,数列 的前n项和为
的前n项和为 ,求证:
,求证: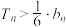 .
.
 的前n项的和为
的前n项的和为 ,
,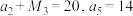 .数列
.数列 的前n项和为
的前n项和为 ,
,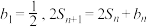 .
.(1)求数列
 和
和 的通项公式;
的通项公式;(2)若
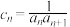 ,数列
,数列 的前n项和为
的前n项和为 ,求证:
,求证: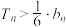 .
.
您最近一年使用:0次
2022-12-12更新
|
1081次组卷
|
3卷引用:辽宁省大连育明高级中学2022-2023学年高三下学期一模数学试题
名校
解题方法
10 . 若正项数列 满足
满足 ,则
,则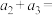 ( )
( )
 满足
满足 ,则
,则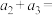 ( )
( )A.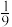 | B.1 | C.6 | D.12 |
您最近一年使用:0次
2023-04-04更新
|
719次组卷
|
6卷引用:辽宁省抚顺市重点高中2022-2023学年高三上学期12月考试数学试题
辽宁省抚顺市重点高中2022-2023学年高三上学期12月考试数学试题山东省2022-2023学年高二10月联合调考数学试题B(已下线)4.3.1 等比数列的概念(精讲)黑龙江省鹤岗市第一中学2022-2023学年高二下学期第一次月考数学试题(已下线)专题6 等比数列的判断(证明)方法 微点4 等比数列的判断(证明)综合训练人教A版(2019) 选修第二册 数学奇书 第四章 数列 阶段测评(二)(4.3)



