名校
解题方法
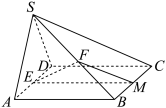
1 . 如图,在四棱锥 中,平面
中,平面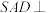 平面
平面 ,
, 为等边三角形,底面
为等边三角形,底面 是平行四边形,点
是平行四边形,点 为
为 的中点,点
的中点,点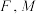 分别在
分别在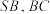 上,且平面
上,且平面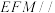 平面
平面 .
. 为线段
为线段 中点;
中点;
(2)若点 在棱
在棱 上,猜想:当
上,猜想:当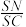 为何值时,有平面
为何值时,有平面 平面
平面 ,并证明你的猜想.
,并证明你的猜想.
 中,平面
中,平面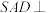 平面
平面 ,
, 为等边三角形,底面
为等边三角形,底面 是平行四边形,点
是平行四边形,点 为
为 的中点,点
的中点,点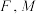 分别在
分别在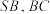 上,且平面
上,且平面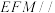 平面
平面 .
.
 为线段
为线段 中点;
中点;(2)若点
 在棱
在棱 上,猜想:当
上,猜想:当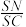 为何值时,有平面
为何值时,有平面 平面
平面 ,并证明你的猜想.
,并证明你的猜想.
您最近一年使用:0次
名校
解题方法
2 . 如图,在四棱柱 中,四边形
中,四边形 为直角梯形,
为直角梯形,

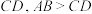 ,
, .过点
.过点 作
作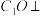 平面
平面 ,垂足为
,垂足为 是
是 的中点.
的中点. 内,过点
内,过点 作
作 ,垂足为
,垂足为 .
.
(i)求证:平面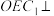 平面
平面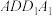 ;
;
(ii)判断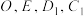 是否共面,并证明.
是否共面,并证明.
(2)在棱 上是否存在一点
上是否存在一点 ,使得
,使得
 平面
平面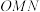 ?若存在,给出证明:若不存在,请说明理由.
?若存在,给出证明:若不存在,请说明理由.
 中,四边形
中,四边形 为直角梯形,
为直角梯形,

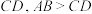 ,
, .过点
.过点 作
作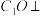 平面
平面 ,垂足为
,垂足为 是
是 的中点.
的中点.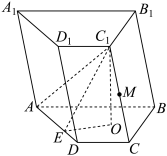
 内,过点
内,过点 作
作 ,垂足为
,垂足为 .
.(i)求证:平面
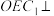 平面
平面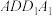 ;
;(ii)判断
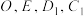 是否共面,并证明.
是否共面,并证明.(2)在棱
 上是否存在一点
上是否存在一点 ,使得
,使得
 平面
平面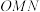 ?若存在,给出证明:若不存在,请说明理由.
?若存在,给出证明:若不存在,请说明理由.
您最近一年使用:0次
2024-07-01更新
|
219次组卷
|
3卷引用:江苏省泰州市2023-2024学年高一下学期6月期末考试数学试题
名校
解题方法
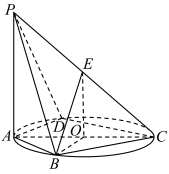
3 . 如图,已知 是圆
是圆 的直径,
的直径, 平面
平面 ,
, 是
是 的中点,
的中点, .
.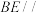 平面
平面 ;
;
(2)求证:平面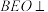 平面
平面 .
.
 是圆
是圆 的直径,
的直径, 平面
平面 ,
, 是
是 的中点,
的中点, .
.
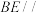 平面
平面 ;
;(2)求证:平面
 平面
平面 .
.
您最近一年使用:0次
解题方法
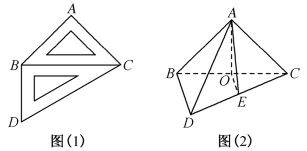
4 . 一副三角板如图(1),将其中的 沿
沿 折起,构造出如图(2)所示的三棱锥,
折起,构造出如图(2)所示的三棱锥, 为
为 的中点,连接
的中点,连接 ,使得
,使得 .
.
(1)取 中点
中点 ,连接
,连接 ,设平面
,设平面 平面
平面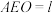 ,求证:
,求证: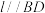 ;
;
(2)证明:平面 ⊥平面
⊥平面 ;
;
(3)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 沿
沿 折起,构造出如图(2)所示的三棱锥,
折起,构造出如图(2)所示的三棱锥, 为
为 的中点,连接
的中点,连接 ,使得
,使得 .
.
(1)取
 中点
中点 ,连接
,连接 ,设平面
,设平面 平面
平面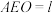 ,求证:
,求证: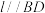 ;
;(2)证明:平面
 ⊥平面
⊥平面 ;
;(3)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
解题方法
5 . 在四棱锥 中,
中, 平面ABCD,
平面ABCD,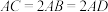 ,
,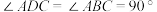 .
.
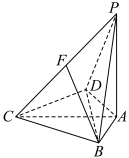
(1)证明: 平面
平面 ;
;
(2)若 是
是 的中点,求证:
的中点,求证: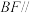 平面
平面 .
.
 中,
中, 平面ABCD,
平面ABCD,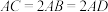 ,
,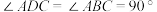 .
.
(1)证明:
 平面
平面 ;
;(2)若
 是
是 的中点,求证:
的中点,求证: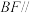 平面
平面 .
.
您最近一年使用:0次
6 . 在平面四边形 中(如图1),
中(如图1),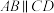 ,
, ,
, ,E是AB中点,现将△ADE沿DE翻折得到四棱锥
,E是AB中点,现将△ADE沿DE翻折得到四棱锥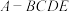 (如图2),
(如图2),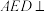 平面
平面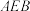 ;
;
(2)图2中,若F是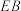 中点,试探究在平面
中点,试探究在平面 内是否存在无数多个点
内是否存在无数多个点 ,都有直线
,都有直线
 平面
平面 ,若存在,请证明.
,若存在,请证明.
 中(如图1),
中(如图1),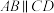 ,
, ,
, ,E是AB中点,现将△ADE沿DE翻折得到四棱锥
,E是AB中点,现将△ADE沿DE翻折得到四棱锥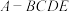 (如图2),
(如图2),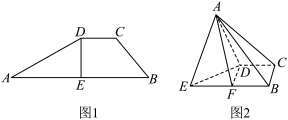
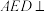 平面
平面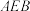 ;
;(2)图2中,若F是
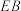 中点,试探究在平面
中点,试探究在平面 内是否存在无数多个点
内是否存在无数多个点 ,都有直线
,都有直线
 平面
平面 ,若存在,请证明.
,若存在,请证明.
您最近一年使用:0次
名校
解题方法
7 . 如图①所示,已知正三角形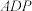 与正方形
与正方形 ,将
,将 沿
沿 翻折至
翻折至 所在的位置,连接
所在的位置,连接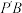 ,
,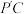 ,得到如图②所示的四棱锥.已知
,得到如图②所示的四棱锥.已知 ,
,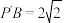 ,
, 为
为 上一点,且满足
上一点,且满足 .
.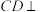 平面
平面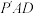 ;
;
(2)在线段 上是否存在一点
上是否存在一点 ,使得
,使得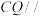 平面
平面 .若存在,指出点
.若存在,指出点 的位置,并证明你的结论;若不存在,请说明理由.
的位置,并证明你的结论;若不存在,请说明理由.
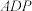 与正方形
与正方形 ,将
,将 沿
沿 翻折至
翻折至 所在的位置,连接
所在的位置,连接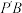 ,
,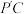 ,得到如图②所示的四棱锥.已知
,得到如图②所示的四棱锥.已知 ,
,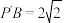 ,
, 为
为 上一点,且满足
上一点,且满足 .
.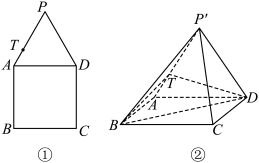
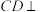 平面
平面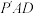 ;
;(2)在线段
 上是否存在一点
上是否存在一点 ,使得
,使得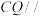 平面
平面 .若存在,指出点
.若存在,指出点 的位置,并证明你的结论;若不存在,请说明理由.
的位置,并证明你的结论;若不存在,请说明理由.
您最近一年使用:0次
2023-04-19更新
|
631次组卷
|
5卷引用:浙江省宁波市北仑中学2022-2023学年高一下学期期中数学试题
浙江省宁波市北仑中学2022-2023学年高一下学期期中数学试题(已下线)立体几何专题:立体几何探索性问题的8种考法(已下线)13.2 基本图形位置关系(分层练习)黑龙江省齐齐哈尔市第八中学校2022-2023学年高一下学期期末数学试题【课后练】专题6翻折问题 课后作业-湘教版(2019)必修(第二册) 第4章 立体几何初步
名校
解题方法
8 . 如图,在三棱柱 中,若G,H分别是线段AC,DF的中点.
中,若G,H分别是线段AC,DF的中点.

 ;
;
(2)在线段CD上是否存在一点 ,使得平面
,使得平面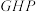
 平面BCF,若存在,指出
平面BCF,若存在,指出 的具体位置并证明;若不存在,说明理由.
的具体位置并证明;若不存在,说明理由.
 中,若G,H分别是线段AC,DF的中点.
中,若G,H分别是线段AC,DF的中点.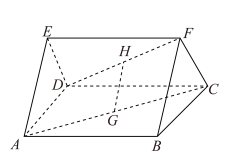


 ;
;(2)在线段CD上是否存在一点
 ,使得平面
,使得平面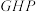
 平面BCF,若存在,指出
平面BCF,若存在,指出 的具体位置并证明;若不存在,说明理由.
的具体位置并证明;若不存在,说明理由.
您最近一年使用:0次
2023-04-13更新
|
3330次组卷
|
11卷引用:浙江省宁波市三锋教研联盟2022-2023学年高一下学期期中联考数学试题
浙江省宁波市三锋教研联盟2022-2023学年高一下学期期中联考数学试题(已下线)立体几何专题:立体几何探索性问题的8种考法(已下线)13.2.4 平面与平面的位置关系 (1)河北定州中学2022-2023学年高一下学期5月月考数学试题江西省宜春市第十中学2024届高二上学期开学检测数学试题新疆阿克苏市实验中学2022-2023学年高一下学期第三次月考数学试题(已下线)8.5.3 平面与平面平行【第三练】“上好三节课,做好三套题“高中数学素养晋级之路(已下线)11.3.3平面与平面平行-同步精品课堂(人教B版2019必修第四册)(已下线)专题突破:空间几何体的动点探究问题-同步题型分类归纳讲与练(人教A版2019必修第二册)【课后练】第4.4节综合训练 课后作业-湘教版(2019)必修(第二册) 第4章 立体几何初步(已下线)第四节直线、平面平行的判定与性质【同步课时】基础卷
名校
解题方法
9 . 如图甲,在四边形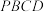 中,
中,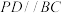 ,
, .现将
.现将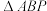 沿
沿 折起得图乙,点
折起得图乙,点 是
是 的中点,点
的中点,点 是
是 的中点.
的中点.

(1)求证: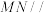 平面
平面 ;
;
(2)在图乙中,过直线 作一平面,与平面
作一平面,与平面 平行,且分别交
平行,且分别交 、
、 于点
于点 、
、 ,注明
,注明 、
、 的位置,并证明.
的位置,并证明.
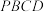 中,
中,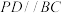 ,
, .现将
.现将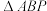 沿
沿 折起得图乙,点
折起得图乙,点 是
是 的中点,点
的中点,点 是
是 的中点.
的中点.
(1)求证:
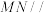 平面
平面 ;
;(2)在图乙中,过直线
 作一平面,与平面
作一平面,与平面 平行,且分别交
平行,且分别交 、
、 于点
于点 、
、 ,注明
,注明 、
、 的位置,并证明.
的位置,并证明.
您最近一年使用:0次
名校
解题方法
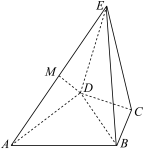
10 . 几何体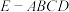 是四棱锥,
是四棱锥, 为正三角形,
为正三角形,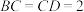 ,
,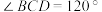 ,
, 为线段
为线段 的中点.
的中点.
(1)求证: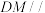 平面
平面 ;
;
(2)线段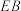 上是否存在一点
上是否存在一点 ,使得
,使得 四点共面?若存在,请找出点
四点共面?若存在,请找出点 ,并证明;若不存在,并说明理由.
,并证明;若不存在,并说明理由.
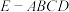 是四棱锥,
是四棱锥, 为正三角形,
为正三角形,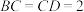 ,
,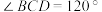 ,
, 为线段
为线段 的中点.
的中点. 
(1)求证:
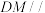 平面
平面 ;
;(2)线段
 上是否存在一点
上是否存在一点 ,使得
,使得 四点共面?若存在,请找出点
四点共面?若存在,请找出点 ,并证明;若不存在,并说明理由.
,并证明;若不存在,并说明理由.
您最近一年使用:0次
2022-11-03更新
|
1024次组卷
|
4卷引用:四川省峨眉第二中学校2022-2023学年高二上学期10月月考理科数学试题
四川省峨眉第二中学校2022-2023学年高二上学期10月月考理科数学试题黑龙江省哈尔滨市宾县第二中学2022-2023学年高三上学期期中考试数学试题(已下线)8.5.3平面与平面平行(精练)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)(已下线)第26讲 空间直线、平面的平行的判定4种常见方法



