2023高二上·全国·专题练习
1 . 如图所示,已知多面体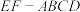 中,四边形
中,四边形 为菱形,
为菱形,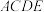 为正四面体,且
为正四面体,且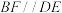 .
.

(1)证明: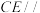 平面ABF;
平面ABF;
(2)求二面角 的余弦值.
的余弦值.
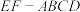 中,四边形
中,四边形 为菱形,
为菱形,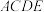 为正四面体,且
为正四面体,且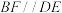 .
.
(1)证明:
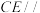 平面ABF;
平面ABF;(2)求二面角
 的余弦值.
的余弦值.
您最近一年使用:0次
名校
2 . 五棱锥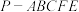 中,
中,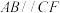 ,
,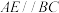 ,
, ,
, ,
,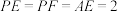 ,
,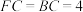 ,
, ,平面
,平面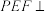 平面
平面 ,
, 为
为 的中点,
的中点,
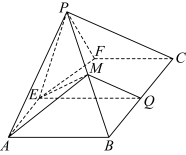
(1)求证: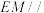 平面
平面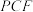 ;
;
(2)求直线 与平面
与平面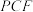 所成角的正弦值.
所成角的正弦值.
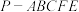 中,
中,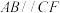 ,
,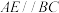 ,
, ,
, ,
,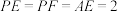 ,
,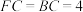 ,
, ,平面
,平面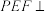 平面
平面 ,
, 为
为 的中点,
的中点,
(1)求证:
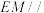 平面
平面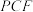 ;
;(2)求直线
 与平面
与平面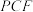 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
解题方法
3 . 如图,正方形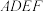 与梯形
与梯形 所在平面互相垂直,已知.
所在平面互相垂直,已知. //
// ,
, ,
,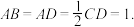 点P为线段EC的中点.
点P为线段EC的中点.

(1)求证: ∥平面CDE;
∥平面CDE;
(2)求直线DP与平面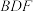 所成角的正弦值;
所成角的正弦值;
(3)求平面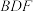 与平面
与平面 夹角的余弦值.
夹角的余弦值.
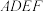 与梯形
与梯形 所在平面互相垂直,已知.
所在平面互相垂直,已知. //
// ,
, ,
,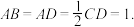 点P为线段EC的中点.
点P为线段EC的中点.
(1)求证:
 ∥平面CDE;
∥平面CDE;(2)求直线DP与平面
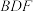 所成角的正弦值;
所成角的正弦值;(3)求平面
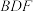 与平面
与平面 夹角的余弦值.
夹角的余弦值.
您最近一年使用:0次
2024高三·全国·专题练习
解题方法
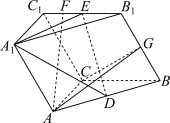
4 . 如图,在三棱柱 中,侧面
中,侧面 是矩形,侧面
是矩形,侧面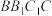 是菱形,
是菱形,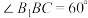 ,
, 、
、 分别为棱
分别为棱 、
、 的中点,
的中点, 为线段
为线段 的中点.证明:
的中点.证明: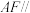 平面
平面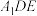 .
.
 中,侧面
中,侧面 是矩形,侧面
是矩形,侧面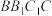 是菱形,
是菱形,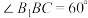 ,
, 、
、 分别为棱
分别为棱 、
、 的中点,
的中点, 为线段
为线段 的中点.证明:
的中点.证明: 平面
平面 .
.
您最近一年使用:0次
2023-11-12更新
|
674次组卷
|
7卷引用:第03讲 直线、平面平行的判定与性质(八大题型)(讲义)
(已下线)第03讲 直线、平面平行的判定与性质(八大题型)(讲义)(已下线)第10讲 8.5.3 平面与平面平行-【帮课堂】(人教A版2019必修第二册)(已下线)13.2.3 直线与平面的位置关系(1)-【帮课堂】(苏教版2019必修第二册)(已下线)11.3.3平面与平面平行-同步精品课堂(人教B版2019必修第四册)(已下线)专题3.5空间直线、平面的平行-重难点突破及混淆易错规避(人教A版2019必修第二册)(已下线)8.5.3 平面与平面平行-同步精品课堂(人教A版2019必修第二册)(已下线)11.3.3 平面与平面平行-【帮课堂】(人教B版2019必修第四册)
名校
5 . 如图,多面体 中,四边形
中,四边形 为矩形,二面角
为矩形,二面角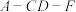 的大小为
的大小为 ,
,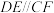 ,
, ,
,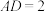 ,
,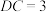 .
.
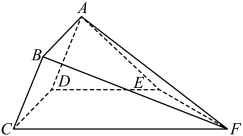
(1)求证: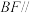 平面
平面 ;
;
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,四边形
中,四边形 为矩形,二面角
为矩形,二面角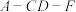 的大小为
的大小为 ,
,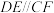 ,
, ,
,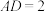 ,
,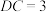 .
.
(1)求证:
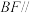 平面
平面 ;
;(2)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2023-06-12更新
|
835次组卷
|
4卷引用:湖南省长沙市第一中学2022-2023学年高一下学期第二次阶段性检测数学试题
湖南省长沙市第一中学2022-2023学年高一下学期第二次阶段性检测数学试题(已下线)第04讲 利用几何法解决空间角和距离19种常见考法归类(2)广东省深圳外国语学校2024届高三上学期第一次月考(入学考试)数学试题广东省深圳外国语学校2023届高三上学期第一次月考(入学测试)数学试题
6 . 如图,在四面体 中,
中,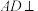 平面
平面 ,
, 是
是 的中点,
的中点, 是
是 的中点,
的中点, 是线段
是线段 上的一点,
上的一点,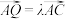 .
.

(1)若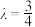 ,证明:
,证明: 平面
平面 ;
;
(2)若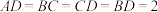 ,且二面角
,且二面角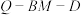 为直二面角,求实数
为直二面角,求实数 的值.
的值.
 中,
中,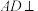 平面
平面 ,
, 是
是 的中点,
的中点, 是
是 的中点,
的中点, 是线段
是线段 上的一点,
上的一点,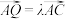 .
.
(1)若
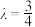 ,证明:
,证明: 平面
平面 ;
;(2)若
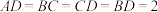 ,且二面角
,且二面角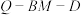 为直二面角,求实数
为直二面角,求实数 的值.
的值.
您最近一年使用:0次
2023高三·全国·专题练习
解题方法
7 . 在矩形ABCD中, ,
,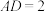 .点E,F分别在AB,CD上,点
.点E,F分别在AB,CD上,点 分别在
分别在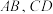 上,且
上,且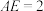 ,
,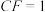 .沿EF将四边形AEFD翻折至四边形
.沿EF将四边形AEFD翻折至四边形 ,点
,点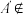 平面BCFE.
平面BCFE.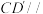 平面
平面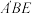 ;
;
(2)求证: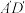 与BC是异面直线;
与BC是异面直线;
 ,
,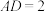 .点E,F分别在AB,CD上,点
.点E,F分别在AB,CD上,点 分别在
分别在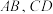 上,且
上,且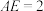 ,
,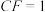 .沿EF将四边形AEFD翻折至四边形
.沿EF将四边形AEFD翻折至四边形 ,点
,点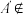 平面BCFE.
平面BCFE.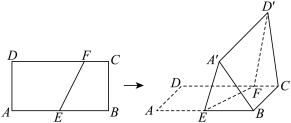
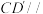 平面
平面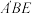 ;
;(2)求证:
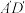 与BC是异面直线;
与BC是异面直线;
您最近一年使用:0次
名校
解题方法
8 . 如图所示,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.
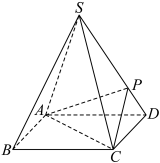
(1)求证:AC⊥SD;
(2)若SD 平面PAC,则侧棱SC上是否存在一点E,使得BE
平面PAC,则侧棱SC上是否存在一点E,使得BE 平面PAC?若存在,求SE∶EC的值;若不存在,试说明理由.
平面PAC?若存在,求SE∶EC的值;若不存在,试说明理由.
 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.
(1)求证:AC⊥SD;
(2)若SD
 平面PAC,则侧棱SC上是否存在一点E,使得BE
平面PAC,则侧棱SC上是否存在一点E,使得BE 平面PAC?若存在,求SE∶EC的值;若不存在,试说明理由.
平面PAC?若存在,求SE∶EC的值;若不存在,试说明理由.
您最近一年使用:0次
2023-06-11更新
|
354次组卷
|
2卷引用:江苏省盐城中学2022-2023学年高二下学期期中数学试题
解题方法
9 . 如图所示,在圆锥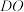 中,
中, 为圆锥的顶点,
为圆锥的顶点, 为底面圆圆心,
为底面圆圆心, 是圆
是圆 的直径,
的直径, 为底面圆周上一点,四边形
为底面圆周上一点,四边形 是矩形.
是矩形.

(1)若点 是
是 的中点,求证:
的中点,求证: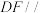 平面
平面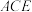 ;
;
(2)若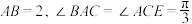 ,求三棱锥
,求三棱锥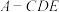 的体积.
的体积.
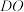 中,
中, 为圆锥的顶点,
为圆锥的顶点, 为底面圆圆心,
为底面圆圆心, 是圆
是圆 的直径,
的直径, 为底面圆周上一点,四边形
为底面圆周上一点,四边形 是矩形.
是矩形.
(1)若点
 是
是 的中点,求证:
的中点,求证: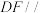 平面
平面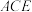 ;
;(2)若
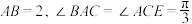 ,求三棱锥
,求三棱锥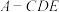 的体积.
的体积.
您最近一年使用:0次
名校
解题方法
10 . 如图, 平面
平面 ,
, ,
,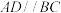 ,
, ,
,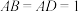 ,
, .
.

(1)求证: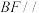 平面
平面 ;
;
(2)求平面 与平面
与平面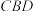 夹角的余弦值;
夹角的余弦值;
(3)若点E到平面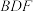 的距离为
的距离为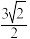 ,求三棱锥
,求三棱锥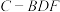 的体积.
的体积.
 平面
平面 ,
, ,
,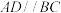 ,
, ,
,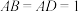 ,
, .
.
(1)求证:
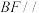 平面
平面 ;
;(2)求平面
 与平面
与平面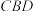 夹角的余弦值;
夹角的余弦值;(3)若点E到平面
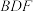 的距离为
的距离为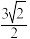 ,求三棱锥
,求三棱锥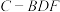 的体积.
的体积.
您最近一年使用:0次



