名校
1 . 如图,在直四棱柱 中,
中, .
.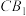
 平面
平面 ;
;
(2)求 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.
 中,
中, .
.
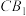
 平面
平面 ;
;(2)求
 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.
您最近一年使用:0次
名校
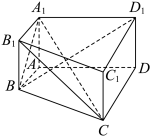
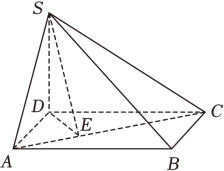
2 . “阳马”是我国古代数学名著《九章算术》中《商功》章节研究的一种几何体,即其底面为矩形,一条侧棱垂直于底面的四棱锥.如图,四边形 是边长为3的正方形,
是边长为3的正方形,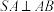 ,
, .
. 是一个“阳马”;
是一个“阳马”;
(2)已知点 在线段
在线段 上,且
上,且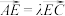 ,若二面角
,若二面角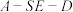 的余弦值为
的余弦值为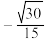 ,求
,求 的值.
的值.
 是边长为3的正方形,
是边长为3的正方形,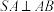 ,
, .
.
 是一个“阳马”;
是一个“阳马”;(2)已知点
 在线段
在线段 上,且
上,且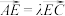 ,若二面角
,若二面角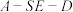 的余弦值为
的余弦值为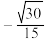 ,求
,求 的值.
的值.
您最近一年使用:0次
2024-06-20更新
|
535次组卷
|
3卷引用:山东省青岛市部分学校2023-2024学年高二下学期联合数学模拟题
名校
解题方法
3 . 在正方体 中,平面
中,平面 经过点
经过点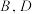 ,平面
,平面 经过点
经过点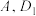 ,当平面
,当平面 分别截正方体所得截面面积最大时,平面
分别截正方体所得截面面积最大时,平面 与平面
与平面 的夹角的余弦值为( )
的夹角的余弦值为( )
 中,平面
中,平面 经过点
经过点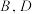 ,平面
,平面 经过点
经过点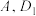 ,当平面
,当平面 分别截正方体所得截面面积最大时,平面
分别截正方体所得截面面积最大时,平面 与平面
与平面 的夹角的余弦值为( )
的夹角的余弦值为( )A. | B. | C. | D.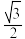 |
您最近一年使用:0次
2024-06-04更新
|
331次组卷
|
5卷引用:江西省上高二中2024届高三适应性考试数学试卷
江西省上高二中2024届高三适应性考试数学试卷(已下线)1.4.2用空间向量研究距离、夹角问题——课后作业(基础版)云南省临沧市云县2023-2024学年高二下学期期末考试数学试卷(已下线)1.2.4 二面角——课后作业(提升版)(已下线)核心考点2 空间向量的应用 B提升卷 (高二期中考试必考的核心考点)
名校
4 . 如图,已知四棱台 的上、下底面分别是边长为2和4的正方形,平面
的上、下底面分别是边长为2和4的正方形,平面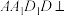 平面
平面 ,
,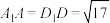 ,点
,点 是棱
是棱 的中点,点
的中点,点 在棱
在棱 上.
上. 点在什么位置时,使得
点在什么位置时,使得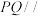 平面
平面 ;
;
(2)若面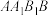 与面
与面 所成角的正弦值为
所成角的正弦值为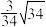 ,求
,求 的长.
的长.
 的上、下底面分别是边长为2和4的正方形,平面
的上、下底面分别是边长为2和4的正方形,平面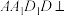 平面
平面 ,
,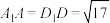 ,点
,点 是棱
是棱 的中点,点
的中点,点 在棱
在棱 上.
上.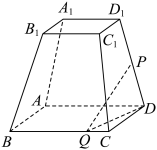
 点在什么位置时,使得
点在什么位置时,使得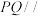 平面
平面 ;
;(2)若面
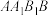 与面
与面 所成角的正弦值为
所成角的正弦值为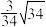 ,求
,求 的长.
的长.
您最近一年使用:0次
2024-05-08更新
|
399次组卷
|
3卷引用:四川省成都外国语学校2023-2024学年高二下学期零诊模拟数学试题
四川省成都外国语学校2023-2024学年高二下学期零诊模拟数学试题江苏省盐城市三校2023-2024学年高二下学期4月期中联考数学试题(已下线)作业01 空间向量与立体几何-【暑假分层作业】(苏教版2019选择性必修第二册)
名校
5 . 如图,在直三棱柱 中,
中,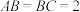 ,
, ,点
,点 ,
, 分别在棱
分别在棱 ,
, 上,
上,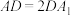 ,
, ,
, 为
为 的中点.
的中点.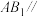 平面
平面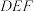 ;
;
(2)当三棱柱 的体积最大时,求平面
的体积最大时,求平面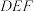 与平面
与平面 夹角的余弦值.
夹角的余弦值.
 中,
中,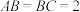 ,
, ,点
,点 ,
, 分别在棱
分别在棱 ,
, 上,
上,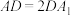 ,
, ,
, 为
为 的中点.
的中点.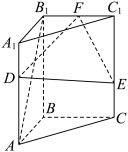
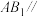 平面
平面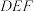 ;
;(2)当三棱柱
 的体积最大时,求平面
的体积最大时,求平面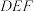 与平面
与平面 夹角的余弦值.
夹角的余弦值.
您最近一年使用:0次
2024-04-29更新
|
963次组卷
|
3卷引用:江西省上高二中2024届高三适应性考试数学试卷
江西省上高二中2024届高三适应性考试数学试卷湖南省长郡中学、浙江省杭州二中、江苏省南京师大附中三校2023-2024学年高三下学期联考数学试题(已下线)2024年高考全国甲卷数学(理)真题平行卷(提升)
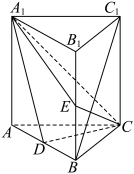
6 . 如图,直三棱柱 中,
中, ,
, 分别是
分别是 ,
, 的中点,
的中点,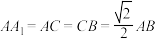 .
.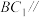 平面
平面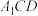 ;
;
(2)求异面直线 和
和 所成角的大小;
所成角的大小;
 中,
中, ,
, 分别是
分别是 ,
, 的中点,
的中点,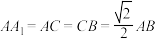 .
.
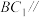 平面
平面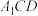 ;
;(2)求异面直线
 和
和 所成角的大小;
所成角的大小;
您最近一年使用:0次
2017-02-08更新
|
587次组卷
|
2卷引用:2024年湖南省普通高中学业水平合格性考试(压轴卷)数学试题



