1 . 抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为阿基米德三角形,该三角形以其深刻的背景、丰富的性质产生了无穷的魅力.设抛物线 (
( ),弦
),弦 过焦点
过焦点 ,
, 为其阿基米德三角形,则下列结论一定成立的是( )
为其阿基米德三角形,则下列结论一定成立的是( )
 (
( ),弦
),弦 过焦点
过焦点 ,
, 为其阿基米德三角形,则下列结论一定成立的是( )
为其阿基米德三角形,则下列结论一定成立的是( )A.点 在抛物线 在抛物线 ( ( )的准线 )的准线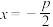 上 上 |
B.存在点 ,使得 ,使得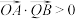 |
C.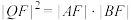 |
D. 面积的最小值为 面积的最小值为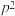 |
您最近一年使用:0次
21-22高二上·全国·单元测试
名校
解题方法
2 . 抛物线的弦与过弦的端点的两条切线所围成的三角形称为阿基米德三角形.设抛物线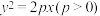 ,弦
,弦 过焦点
过焦点 为其阿基米德三角形,则下列结论一定成立的是( )
为其阿基米德三角形,则下列结论一定成立的是( )
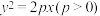 ,弦
,弦 过焦点
过焦点 为其阿基米德三角形,则下列结论一定成立的是( )
为其阿基米德三角形,则下列结论一定成立的是( )A.存在点 ,使得 ,使得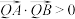 |
B.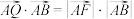 |
C.对于任意的点 ,必有向量 ,必有向量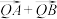 与向量 与向量 共线 共线 |
D. 面积的最小值为 面积的最小值为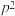 |
您最近一年使用:0次
2023-05-24更新
|
751次组卷
|
8卷引用:专题17 圆锥曲线常考压轴小题全归类(16大核心考点)(讲义)
(已下线)专题17 圆锥曲线常考压轴小题全归类(16大核心考点)(讲义)(已下线)专题1 千年古图 巧用定理 练(已下线)卷07 圆锥曲线的方程——章节重难点突破卷-【重难点突破】2021-2022学年高二数学上册常考题专练(人教A版2019选择性必修第一册)重庆市南开中学校2021-2022学年高二上学期11月月考数学试题(已下线)第十一章 圆锥曲线专练18—抛物线综合练习2-2022届高三数学一轮复习湖北省武汉市第十一中学2021-2022学年高二上学期12月月考数学试题(已下线)专题3 阿基米德三角形 微点2 阿基米德三角形综合训练山东省普通高中2023届高三模拟演练数学试题
名校
解题方法
3 . 抛物线有如下光学性质:过焦点的光线经抛物线反射后得到的光线平行于抛物线的对称轴;反之,平行于抛物线对称轴的入射光线经抛物线反射后得到的光线必过抛物线的焦点.已知抛物线 的焦点为F,一条平行于x轴的光线从点
的焦点为F,一条平行于x轴的光线从点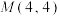 射出,经过抛物线上的点A反射后,到达抛物线上的点B,则
射出,经过抛物线上的点A反射后,到达抛物线上的点B,则
___________ .
 的焦点为F,一条平行于x轴的光线从点
的焦点为F,一条平行于x轴的光线从点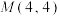 射出,经过抛物线上的点A反射后,到达抛物线上的点B,则
射出,经过抛物线上的点A反射后,到达抛物线上的点B,则
您最近一年使用:0次
2022-11-26更新
|
518次组卷
|
4卷引用:天津市滨海新区2023-2024学年高二上学期期末质量检测数学试题
名校
4 . 我们把圆锥曲线的弦 与过弦的端点
与过弦的端点 ,
, 处的两条切线所围成的三角形
处的两条切线所围成的三角形 (
( 为两切线的交点)叫做“阿基米德三角形”,抛物线有一类特殊的“阿基米德三角形”,当线段
为两切线的交点)叫做“阿基米德三角形”,抛物线有一类特殊的“阿基米德三角形”,当线段 经过抛物线的焦点
经过抛物线的焦点 时,
时, 具有以下性质:①
具有以下性质:① 点必在抛物线的准线上;②
点必在抛物线的准线上;② ;③
;③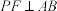 .已知直线
.已知直线 :
: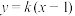 与抛物线
与抛物线 :
: 交于
交于 ,
, 点,若
点,若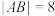 ,记此时抛物线
,记此时抛物线  的“阿基米德三角形”为
的“阿基米德三角形”为 ,则
,则 点为( )
点为( )
 与过弦的端点
与过弦的端点 ,
, 处的两条切线所围成的三角形
处的两条切线所围成的三角形 (
( 为两切线的交点)叫做“阿基米德三角形”,抛物线有一类特殊的“阿基米德三角形”,当线段
为两切线的交点)叫做“阿基米德三角形”,抛物线有一类特殊的“阿基米德三角形”,当线段 经过抛物线的焦点
经过抛物线的焦点 时,
时, 具有以下性质:①
具有以下性质:① 点必在抛物线的准线上;②
点必在抛物线的准线上;② ;③
;③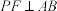 .已知直线
.已知直线 :
: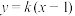 与抛物线
与抛物线 :
: 交于
交于 ,
, 点,若
点,若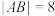 ,记此时抛物线
,记此时抛物线  的“阿基米德三角形”为
的“阿基米德三角形”为 ,则
,则 点为( )
点为( )A.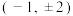 | B.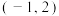 |
C.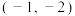 | D.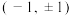 |
您最近一年使用:0次
5 . 阿基米德(公元前287年~公元前212年)是古希腊伟大的物理学家,数学家和天文学家,并享有“数学之神”的称号.他研究抛物线的求积法,得出了著名的阿基米德定理.在该定理中,抛物线的弦与过弦的端点的两切线所围成的三角形被称为“阿基米德三角形”.若抛物线上任意两点 处的切线交于点
处的切线交于点 ,则
,则 为“阿基米德三角形”,且当线段
为“阿基米德三角形”,且当线段 经过抛物线的焦点
经过抛物线的焦点 时,
时, 具有以下特征:(1)
具有以下特征:(1) 点必在抛物线的准线上;(2)
点必在抛物线的准线上;(2) ;(3)
;(3)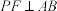 .若经过抛物线
.若经过抛物线 的焦点的一条弦为
的焦点的一条弦为 ,“阿基米德三角形”为
,“阿基米德三角形”为 ,且点
,且点 在直线
在直线 上,则直线
上,则直线 的方程为( )
的方程为( )
 处的切线交于点
处的切线交于点 ,则
,则 为“阿基米德三角形”,且当线段
为“阿基米德三角形”,且当线段 经过抛物线的焦点
经过抛物线的焦点 时,
时, 具有以下特征:(1)
具有以下特征:(1) 点必在抛物线的准线上;(2)
点必在抛物线的准线上;(2) ;(3)
;(3)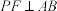 .若经过抛物线
.若经过抛物线 的焦点的一条弦为
的焦点的一条弦为 ,“阿基米德三角形”为
,“阿基米德三角形”为 ,且点
,且点 在直线
在直线 上,则直线
上,则直线 的方程为( )
的方程为( )A. | B. |
C. | D. |
您最近一年使用:0次
2022-01-22更新
|
804次组卷
|
4卷引用:四川省眉山市青神中学校2023-2024学年高二上学期期末模拟数学试题
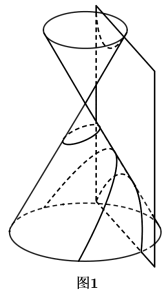
6 . 古希腊数学家阿波罗尼奥斯采用平面切割圆锥的方法来研究曲线,如图①,用一个不垂直于圆锥的轴的平面截圆锥,当圆锥与截面所成的角不同时,可以得到不同的截口曲线,它们分别是椭圆、抛物线和双曲线.图②,在底面半径和高均为 的圆锥中,
的圆锥中, 、
、 是底面圆
是底面圆 的两条互相垂直的直径,
的两条互相垂直的直径, 是母线
是母线 的中点,
的中点, 是线段
是线段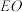 的中点,已知过
的中点,已知过 与
与 的平面与圆锥侧面的交线是以E为顶点的圆锥曲线的一部分,则该曲线为
的平面与圆锥侧面的交线是以E为顶点的圆锥曲线的一部分,则该曲线为____________ , 是该曲线上的两点且
是该曲线上的两点且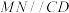 ,若
,若 经过点
经过点 ,则
,则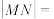
__________ .
 的圆锥中,
的圆锥中, 、
、 是底面圆
是底面圆 的两条互相垂直的直径,
的两条互相垂直的直径, 是母线
是母线 的中点,
的中点, 是线段
是线段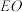 的中点,已知过
的中点,已知过 与
与 的平面与圆锥侧面的交线是以E为顶点的圆锥曲线的一部分,则该曲线为
的平面与圆锥侧面的交线是以E为顶点的圆锥曲线的一部分,则该曲线为 是该曲线上的两点且
是该曲线上的两点且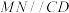 ,若
,若 经过点
经过点 ,则
,则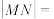

您最近一年使用:0次
2021-06-22更新
|
1401次组卷
|
7卷引用:【一题多变】圆锥曲线 缘何为此
(已下线)【一题多变】圆锥曲线 缘何为此广东省佛山市五校联盟2021届高三5月数学模拟考试试题(已下线)专题05 平面解析几何-2021年高考真题和模拟题数学(文)分项汇编(全国通用)(已下线)热点08 立体几何-2022年高考数学【热点·重点·难点】专练(新高考专用)(已下线)专题8-2 立体几何截面问题的十种题型-2022年高考数学毕业班二轮热点题型归纳与变式演练(全国通用)(已下线)NO.3 练悟专区——客观题满分练 (二)-2022年高考数学二轮复习讲练测(新教材·新高考地区专用)沪教版(2020) 选修第一册 新课改一课一练 期中测试B
名校
解题方法
7 . 过抛物线 的焦点
的焦点 作抛物线的弦与抛物线交于
作抛物线的弦与抛物线交于 、
、 两点,
两点, 为
为 的中点,分别过
的中点,分别过 、
、 两点作抛物线的切线
两点作抛物线的切线 、
、 相交于点
相交于点 .
. 又常被称作阿基米德三角形.下面关于
又常被称作阿基米德三角形.下面关于 的描述:
的描述:
① 点必在抛物线的准线上;
点必在抛物线的准线上;
② ;
;
③设 、
、 ,则
,则 的面积
的面积 的最小值为
的最小值为 ;
;
④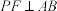 ;
;
⑤ 平行于
平行于 轴.
轴.
其中正确的个数是( )
 的焦点
的焦点 作抛物线的弦与抛物线交于
作抛物线的弦与抛物线交于 、
、 两点,
两点, 为
为 的中点,分别过
的中点,分别过 、
、 两点作抛物线的切线
两点作抛物线的切线 、
、 相交于点
相交于点 .
. 又常被称作阿基米德三角形.下面关于
又常被称作阿基米德三角形.下面关于 的描述:
的描述:①
 点必在抛物线的准线上;
点必在抛物线的准线上;②
 ;
;③设
 、
、 ,则
,则 的面积
的面积 的最小值为
的最小值为 ;
;④
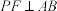 ;
;⑤
 平行于
平行于 轴.
轴.其中正确的个数是( )
A. | B. | C. | D. |
您最近一年使用:0次
2020-11-05更新
|
2071次组卷
|
4卷引用:专题1 千年古图 巧用定理 练
(已下线)专题1 千年古图 巧用定理 练云南师范大学附属中学2021届高三高考适应性月考卷(一)数学(理)试题云南师大附中2021届高三高考适应性月考卷(一)理科数学试题(已下线)专题3 阿基米德三角形 微点2 阿基米德三角形综合训练
名校
8 . 阿基米德(公元前287年~公元前212年)是古希腊伟大的物理学家、数学家和天文学家.他研究抛物线的求积法得出著名的阿基米德定理,并享有“数学之神”的称号.抛物线的弦与过弦的端点的两条切线所围成的三角形被称为阿基米德三角形.如图, 为阿基米德三角形.抛物线
为阿基米德三角形.抛物线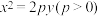 上有两个不同的点
上有两个不同的点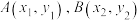 ,以A,B为切点的抛物线的切线
,以A,B为切点的抛物线的切线 相交于P.给出如下结论,其中正确的为( )
相交于P.给出如下结论,其中正确的为( )
(1)若弦 过焦点,则
过焦点,则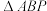 为直角三角形且
为直角三角形且 ;
;
(2)点P的坐标是 ;
;
(3) 的边
的边 所在的直线方程为
所在的直线方程为 ;
;
(4) 的边
的边 上的中线与y轴平行(或重合).
上的中线与y轴平行(或重合).
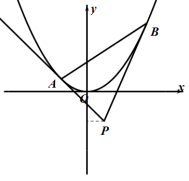
 为阿基米德三角形.抛物线
为阿基米德三角形.抛物线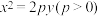 上有两个不同的点
上有两个不同的点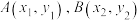 ,以A,B为切点的抛物线的切线
,以A,B为切点的抛物线的切线 相交于P.给出如下结论,其中正确的为( )
相交于P.给出如下结论,其中正确的为( )(1)若弦
 过焦点,则
过焦点,则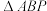 为直角三角形且
为直角三角形且 ;
;(2)点P的坐标是
 ;
;(3)
 的边
的边 所在的直线方程为
所在的直线方程为 ;
;(4)
 的边
的边 上的中线与y轴平行(或重合).
上的中线与y轴平行(或重合).
| A.(2)(3)(4) | B.(1)(2) | C.(1)(2)(3) | D.(1)(3)(4) |
您最近一年使用:0次
2020-07-23更新
|
3490次组卷
|
6卷引用:专题1 千年古图 巧用定理 练
(已下线)专题1 千年古图 巧用定理 练云南师范大学附属中学2020届高三适应性月考(九)数学(文)试题云南师范大学附属中学2020届高三适应性月考(九)数学(理)试题(已下线)专题3 阿基米德三角形 微点2 阿基米德三角形综合训练(已下线)专题9 圆锥曲线第二定义的应用 微点3 圆锥曲线第二定义的应用综合训练(已下线)专题12 圆锥曲线压轴小题常见题型全归纳(精讲精练)-1



