2024·全国·模拟预测
名校
1 . 甲、乙两人进行象棋比赛,赛前每人有3面小红旗.一局比赛后输者需给赢者一面小红旗;若是平局不需要给红旗,当其中一方无小红旗时,比赛结束,有6面小红旗者最终获胜.根据以往的两人比赛结果可知,在一局比赛中甲胜的概率为0.5,乙胜的概率为0.4.
(1)若第一局比赛后甲的红旗个数为X,求X的分布列和数学期望;
(2)若比赛一共进行五局,求第一局是乙胜的条件下,甲最终获胜的概率(结果保留两位有效数字);
(3)记甲获得红旗为 面时最终甲获胜的概率为
面时最终甲获胜的概率为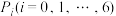 ,
,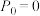 ,
,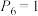 ,证明:
,证明: 为等比数列.
为等比数列.
(1)若第一局比赛后甲的红旗个数为X,求X的分布列和数学期望;
(2)若比赛一共进行五局,求第一局是乙胜的条件下,甲最终获胜的概率(结果保留两位有效数字);
(3)记甲获得红旗为
 面时最终甲获胜的概率为
面时最终甲获胜的概率为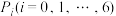 ,
,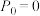 ,
,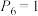 ,证明:
,证明: 为等比数列.
为等比数列.
您最近一年使用:0次
名校
解题方法
2 . 某商城进行促销活动,购买某产品的顾客可以参加一次游戏:在一个不透明箱子中放入红、蓝、黄三种颜色的小球各1个,顾客从中有放回地取出小球,直到取出的小球集齐了三种颜色则停止取球.设顾客停止取球时,取过的小球次数为 ,
,
(1)求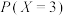 ;
;
(2)设 ,数列
,数列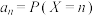 ,求
,求 的通项公式;
的通项公式;
(3)顾客停止取球时,取过的小球次数为 ,顾客可以获得对应的
,顾客可以获得对应的 元奖金,其中
元奖金,其中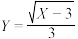 ,求证:
,求证: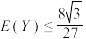 .
.
 ,
,(1)求
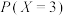 ;
;(2)设
 ,数列
,数列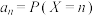 ,求
,求 的通项公式;
的通项公式;(3)顾客停止取球时,取过的小球次数为
 ,顾客可以获得对应的
,顾客可以获得对应的 元奖金,其中
元奖金,其中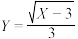 ,求证:
,求证: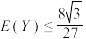 .
.
您最近一年使用:0次
3 . 某商场为促销设计了一项回馈客户的抽奖活动,抽奖规则是:有放回的从装有大小相同的6个红球和4个黑球的袋中任意抽取一个,若第一次抽到红球则奖励50元的奖券,抽到黑球则奖励25元的奖券;第二次开始,每一次抽到红球则奖券数额是上一次奖券数额的2倍,抽到黑球则奖励25元的奖券,记顾客甲第n次抽奖所得的奖券数额 的数学期望为
的数学期望为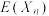 .
.
(1)求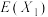 及
及 的分布列.
的分布列.
(2)写出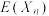 与
与 的递推关系式,并证明
的递推关系式,并证明 为等比数列;
为等比数列;
(3)若顾客甲一共有6次抽奖机会,求该顾客所得的所有奖券数额的期望值.(考数据: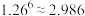 )
)
 的数学期望为
的数学期望为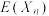 .
.(1)求
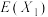 及
及 的分布列.
的分布列.(2)写出
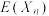 与
与 的递推关系式,并证明
的递推关系式,并证明 为等比数列;
为等比数列;(3)若顾客甲一共有6次抽奖机会,求该顾客所得的所有奖券数额的期望值.(考数据:
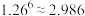 )
)
您最近一年使用:0次
2024-03-08更新
|
755次组卷
|
7卷引用:山东省实验中学2024届高三第一次诊断考试数学试题变式题19-22
(已下线)山东省实验中学2024届高三第一次诊断考试数学试题变式题19-22(已下线)【一题多变】有无放回 两类分布(已下线)微考点7-2 递推方法计算概率与一维马尔科夫过程(数列与概率结合)(已下线)第七章 概率初步(续)(压轴题专练)-2023-2024学年高二数学单元速记·巧练(沪教版2020选择性必修第二册)(已下线)8.2 离散型随机变量及其分布列(4)(已下线)大招1 创新数列交汇问题的速破策略广东省佛山市南海区狮山石门高级中学2024届高三上学期第二次统测(10月)数学试题
名校
4 . 甲、乙、丙、丁四人练习传球,每次由一人随机传给另外三人中的一人称为一次传球,已知甲首先发球,连续传球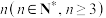 次后,记事件“乙、丙、丁三人均被传到球”的概率为
次后,记事件“乙、丙、丁三人均被传到球”的概率为 .
.
(1)当 时,求球又回到甲手中的概率;
时,求球又回到甲手中的概率;
(2)当 时,记乙、丙、丁三人中被传到球的人数为随机变量
时,记乙、丙、丁三人中被传到球的人数为随机变量 ,求
,求 的分布列与数学期望;
的分布列与数学期望;
(3)记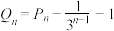 ,求证:数列
,求证:数列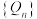 从第3项起构成等比数列,并求
从第3项起构成等比数列,并求 .
.
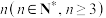 次后,记事件“乙、丙、丁三人均被传到球”的概率为
次后,记事件“乙、丙、丁三人均被传到球”的概率为 .
.(1)当
 时,求球又回到甲手中的概率;
时,求球又回到甲手中的概率;(2)当
 时,记乙、丙、丁三人中被传到球的人数为随机变量
时,记乙、丙、丁三人中被传到球的人数为随机变量 ,求
,求 的分布列与数学期望;
的分布列与数学期望;(3)记
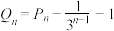 ,求证:数列
,求证:数列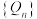 从第3项起构成等比数列,并求
从第3项起构成等比数列,并求 .
.
您最近一年使用:0次
名校
解题方法
5 . 如图是2023年11月1日到11月20日,某地区甲流疫情新增数据的走势图.

(1)从这20天中任选1天,求新增确诊和新增疑似的人数都超过100的概率;
(2)从新增确诊的人数超过100的日期中任选两天,用 表示新增确诊的人数超过140的天数,求
表示新增确诊的人数超过140的天数,求 的分布列和数学期望;
的分布列和数学期望;
(3)记每天新增确诊的人数为 ,每天新增疑似的人数
,每天新增疑似的人数 ,根据这20天统计数据,试判断
,根据这20天统计数据,试判断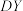 与
与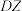 的大小关系(结论不要求证明).
的大小关系(结论不要求证明).

(1)从这20天中任选1天,求新增确诊和新增疑似的人数都超过100的概率;
(2)从新增确诊的人数超过100的日期中任选两天,用
 表示新增确诊的人数超过140的天数,求
表示新增确诊的人数超过140的天数,求 的分布列和数学期望;
的分布列和数学期望;(3)记每天新增确诊的人数为
 ,每天新增疑似的人数
,每天新增疑似的人数 ,根据这20天统计数据,试判断
,根据这20天统计数据,试判断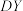 与
与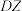 的大小关系(结论不要求证明).
的大小关系(结论不要求证明).
您最近一年使用:0次
2023-12-13更新
|
463次组卷
|
8卷引用:考点12 离散型随机变量的期望和方差 2024届高考数学考点总动员【练】
(已下线)考点12 离散型随机变量的期望和方差 2024届高考数学考点总动员【练】(已下线)7.3.2离散型随机变量的方差(分层练习,8大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)专题7.6 离散型随机变量及其分布大题专项训练【六大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)北京市第一六一中学2024届高三上学期12月阶段测试数学试题7.3.2离散型随机变量的方差(已下线)专题11 离散型随机变量的数字特征(六大考点)-【寒假自学课】2024年高二数学寒假提升学与练(人教A版2019)(已下线)6.3.2离散型随机变量的方差(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)(已下线)专题19 离散型随机变量及其分布列11种常见考法归类(3)
解题方法
6 . 有 个编号分别为
个编号分别为 的盒子,第1个盒子中有2个红球和1个白球,其余盒子中均为1个红球和1个白球,现从第1个盒子中任取一球放入第2个盒子,现从第2个盒子中任取一球放入第3个盒子,
的盒子,第1个盒子中有2个红球和1个白球,其余盒子中均为1个红球和1个白球,现从第1个盒子中任取一球放入第2个盒子,现从第2个盒子中任取一球放入第3个盒子, ,依次进行.
,依次进行.
(1)求从第2个盒子中取到红球的概率;
(2)求从第 个盒子中取到红球的概率;
个盒子中取到红球的概率;
(3)设第 个盒子中红球的个数为
个盒子中红球的个数为 ,
, 的期望值为
的期望值为 ,求证:
,求证: .
.
 个编号分别为
个编号分别为 的盒子,第1个盒子中有2个红球和1个白球,其余盒子中均为1个红球和1个白球,现从第1个盒子中任取一球放入第2个盒子,现从第2个盒子中任取一球放入第3个盒子,
的盒子,第1个盒子中有2个红球和1个白球,其余盒子中均为1个红球和1个白球,现从第1个盒子中任取一球放入第2个盒子,现从第2个盒子中任取一球放入第3个盒子, ,依次进行.
,依次进行.(1)求从第2个盒子中取到红球的概率;
(2)求从第
 个盒子中取到红球的概率;
个盒子中取到红球的概率;(3)设第
 个盒子中红球的个数为
个盒子中红球的个数为 ,
, 的期望值为
的期望值为 ,求证:
,求证: .
.
您最近一年使用:0次
名校
解题方法
7 . 某足球训练基地有编号为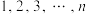 的
的 位学员,在一次射门考核比赛中,学员有两次射门机会.每人第一次射中的概率为
位学员,在一次射门考核比赛中,学员有两次射门机会.每人第一次射中的概率为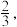 第二次射中的概率为
第二次射中的概率为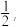 假设每位学员射门过程是相互独立的,比赛规则如下:
假设每位学员射门过程是相互独立的,比赛规则如下:
①按编号从小到大的顺序进行,第1号学员开始第1轮比赛,先第一次射门;
②若第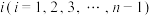 号学员第一次射门未射中,则第
号学员第一次射门未射中,则第 轮比赛失败,由第
轮比赛失败,由第 号学员继续比赛;
号学员继续比赛;
③若第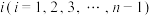 号学员第一次射门射中,再第二次射门,若该学员第二次射门射中,则比赛在第
号学员第一次射门射中,再第二次射门,若该学员第二次射门射中,则比赛在第 轮结束,该学员第二次射门未射中,则第
轮结束,该学员第二次射门未射中,则第 轮比赛失败,由第
轮比赛失败,由第 号学员继续比赛;
号学员继续比赛;
④若比赛进行到了第 轮,则不管第
轮,则不管第 号学员的射门情况,比赛结束.
号学员的射门情况,比赛结束.
(1)当 时,设随机变量
时,设随机变量 表示3名学员在第
表示3名学员在第 轮比赛结束,求随机变量
轮比赛结束,求随机变量 的分布列;
的分布列;
(2)设随机变量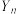 表示
表示 名学员在第
名学员在第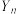 轮比赛结束.
轮比赛结束.
①求随机变量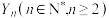 的分布列;
的分布列;
②求证: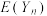 单调递增,且小于3.
单调递增,且小于3.
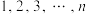 的
的 位学员,在一次射门考核比赛中,学员有两次射门机会.每人第一次射中的概率为
位学员,在一次射门考核比赛中,学员有两次射门机会.每人第一次射中的概率为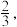 第二次射中的概率为
第二次射中的概率为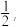 假设每位学员射门过程是相互独立的,比赛规则如下:
假设每位学员射门过程是相互独立的,比赛规则如下:①按编号从小到大的顺序进行,第1号学员开始第1轮比赛,先第一次射门;
②若第
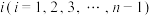 号学员第一次射门未射中,则第
号学员第一次射门未射中,则第 轮比赛失败,由第
轮比赛失败,由第 号学员继续比赛;
号学员继续比赛;③若第
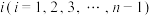 号学员第一次射门射中,再第二次射门,若该学员第二次射门射中,则比赛在第
号学员第一次射门射中,再第二次射门,若该学员第二次射门射中,则比赛在第 轮结束,该学员第二次射门未射中,则第
轮结束,该学员第二次射门未射中,则第 轮比赛失败,由第
轮比赛失败,由第 号学员继续比赛;
号学员继续比赛;④若比赛进行到了第
 轮,则不管第
轮,则不管第 号学员的射门情况,比赛结束.
号学员的射门情况,比赛结束.(1)当
 时,设随机变量
时,设随机变量 表示3名学员在第
表示3名学员在第 轮比赛结束,求随机变量
轮比赛结束,求随机变量 的分布列;
的分布列;(2)设随机变量
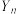 表示
表示 名学员在第
名学员在第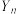 轮比赛结束.
轮比赛结束.①求随机变量
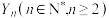 的分布列;
的分布列;②求证:
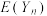 单调递增,且小于3.
单调递增,且小于3.
您最近一年使用:0次
2024高三·全国·专题练习
8 . 掷一枚质地均匀的骰子,得分规则如下:若出现的点数为1,则得1分;若出现的点数为2或3,则得2分;若出现的点数为4或5或6,则得3分.
(1)记 为连续掷这枚骰子2次的总得分,求
为连续掷这枚骰子2次的总得分,求 的数学期望;
的数学期望;
(2)现在将得分规则变更如下:若出现的点数为1或2,则得2分,其他情况都得1分.反复掷这枚骰子,设总得分为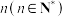 的概率为
的概率为 ,证明:数列
,证明:数列 为等比数列.
为等比数列.
(1)记
 为连续掷这枚骰子2次的总得分,求
为连续掷这枚骰子2次的总得分,求 的数学期望;
的数学期望;(2)现在将得分规则变更如下:若出现的点数为1或2,则得2分,其他情况都得1分.反复掷这枚骰子,设总得分为
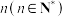 的概率为
的概率为 ,证明:数列
,证明:数列 为等比数列.
为等比数列.
您最近一年使用:0次
解题方法
9 . 某中学为了解本校高二年级学生阅读水平现状,从该年级学生中随机抽取100人进行一般现代文阅读速度的测试,以每位学生平均每分钟阅读的字数作为该学生的阅读速度,将测试结果整理得到如下频率分布直方图:
(2)用频率估计概率,从该校高二学生中随机抽取3人,设这3人中阅读速度达到540字/分钟及以上的人数为 ,求
,求 的分布列与数学期望
的分布列与数学期望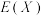 ;
;
(3)若某班有10名学生参加测试,他们的阅读速度如下:506,516,553,592,617,632,667,693,723,776,从这10名学生中随机抽取3人,设这3人中阅读速度达到540字/分钟及以上的人数为 ,试判断数学期望
,试判断数学期望 与(2)中的
与(2)中的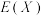 的大小.(结论不要求证明)
的大小.(结论不要求证明)
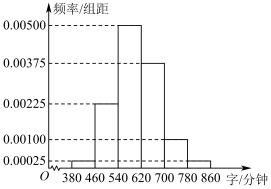
(2)用频率估计概率,从该校高二学生中随机抽取3人,设这3人中阅读速度达到540字/分钟及以上的人数为
 ,求
,求 的分布列与数学期望
的分布列与数学期望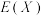 ;
;(3)若某班有10名学生参加测试,他们的阅读速度如下:506,516,553,592,617,632,667,693,723,776,从这10名学生中随机抽取3人,设这3人中阅读速度达到540字/分钟及以上的人数为
 ,试判断数学期望
,试判断数学期望 与(2)中的
与(2)中的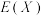 的大小.(结论不要求证明)
的大小.(结论不要求证明)
您最近一年使用:0次
名校
10 . 某单位有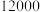 名职工,通过抽验筛查一种疾病的患者.假设患疾病的人在当地人群中的比例为
名职工,通过抽验筛查一种疾病的患者.假设患疾病的人在当地人群中的比例为 .专家建议随机地按
.专家建议随机地按 (
( 且为
且为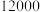 的正因数)人一组分组,然后将各组
的正因数)人一组分组,然后将各组 个人的血样混合再化验. 如果混管血样呈阴性,说明这
个人的血样混合再化验. 如果混管血样呈阴性,说明这 个人全部阴性;如果混管血样呈阳性,说明其中至少有一人的血样呈阳性,就需要对每个人再分别化验一次.设该种方法需要化验的总次数为
个人全部阴性;如果混管血样呈阳性,说明其中至少有一人的血样呈阳性,就需要对每个人再分别化验一次.设该种方法需要化验的总次数为 .
.
(1)当 时,求
时,求 的取值范围并解释其实际意义;
的取值范围并解释其实际意义;
(2)现对混管血样逐一化验,至化验出阳性样本时停止,最多化验 次.记
次.记 为混管的化验次数,当
为混管的化验次数,当 足够大时,证明:
足够大时,证明: ;
;
(3)根据经验预测本次检测时个人患病的概率 ,当
,当 时,按照
时,按照 计算得混管数量
计算得混管数量 的期望
的期望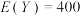 ;某次检验中
;某次检验中 ,试判断个人患病的概率为
,试判断个人患病的概率为 是否合理.(如果
是否合理.(如果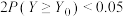 ,则说明假设不合理).
,则说明假设不合理).
附:若 ,则
,则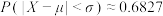 ,
,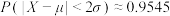 ,
, .
.
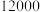 名职工,通过抽验筛查一种疾病的患者.假设患疾病的人在当地人群中的比例为
名职工,通过抽验筛查一种疾病的患者.假设患疾病的人在当地人群中的比例为 .专家建议随机地按
.专家建议随机地按 (
( 且为
且为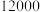 的正因数)人一组分组,然后将各组
的正因数)人一组分组,然后将各组 个人的血样混合再化验. 如果混管血样呈阴性,说明这
个人的血样混合再化验. 如果混管血样呈阴性,说明这 个人全部阴性;如果混管血样呈阳性,说明其中至少有一人的血样呈阳性,就需要对每个人再分别化验一次.设该种方法需要化验的总次数为
个人全部阴性;如果混管血样呈阳性,说明其中至少有一人的血样呈阳性,就需要对每个人再分别化验一次.设该种方法需要化验的总次数为 .
.(1)当
 时,求
时,求 的取值范围并解释其实际意义;
的取值范围并解释其实际意义;(2)现对混管血样逐一化验,至化验出阳性样本时停止,最多化验
 次.记
次.记 为混管的化验次数,当
为混管的化验次数,当 足够大时,证明:
足够大时,证明: ;
;(3)根据经验预测本次检测时个人患病的概率
 ,当
,当 时,按照
时,按照 计算得混管数量
计算得混管数量 的期望
的期望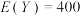 ;某次检验中
;某次检验中 ,试判断个人患病的概率为
,试判断个人患病的概率为 是否合理.(如果
是否合理.(如果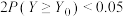 ,则说明假设不合理).
,则说明假设不合理). 附:若
 ,则
,则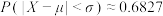 ,
,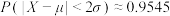 ,
, .
.
您最近一年使用:0次



