名校
解题方法
1 . 如图圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等, ,
, 为圆柱上下底面的圆心,O为球心,EF为底面圆
为圆柱上下底面的圆心,O为球心,EF为底面圆 的一条直径,若球的半径
的一条直径,若球的半径 ,则( )
,则( )
 ,
, 为圆柱上下底面的圆心,O为球心,EF为底面圆
为圆柱上下底面的圆心,O为球心,EF为底面圆 的一条直径,若球的半径
的一条直径,若球的半径 ,则( )
,则( )
A.球与圆柱的体积之比为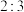 |
B.四面体CDEF的体积的取值范围为 |
C.平面DEF截得球的截面面积最小值为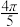 |
D.若P为球面和圆柱侧面的交线上一点,则 的取值范围为 的取值范围为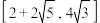 |
您最近一年使用:0次
2023-04-06更新
|
5836次组卷
|
16卷引用:专题05 立体几何
(已下线)专题05 立体几何(已下线)押新高考第11题 立体几何综合(已下线)专题15 球体外接内切综合问题小题(已下线)第四章 立体几何解题通法 专题三 参数法 微点3 参数法综合训练【培优版】浙江省杭州市2023届高三下学期教学质量检测(二模)数学试题江西省景德镇一中2022-2023学年高二(19班)下学期期中考试数学试题重庆市第一中学教育共同体2022-2023学年高一下学期期中数学试题福建省”德化一中、永安一中、漳平一中“三校协作2023届高三适应性考试数学试题福建省安溪一中、养正中学、惠安一中、泉州实验中学2022-2023学年高二下学期期末联考数学试题福建省宁德市福安市阳光国际集团福建区域联考2022-2023学年高一下学期期中数学试题广东省佛山市南海区第一中学2024届高三上学期10月月考数学试题安徽省芜湖市第一中学2022-2023学年高三下学期4月统测数学试卷湖南省长沙市雅礼中学2024届高三4月综合测试数学试题江苏省苏州市南京航空航天大学苏州附属中学2024届高三下学期五月阳光测试数学试题山东省泰安市泰山国际学校2023-2024学年高一下学期期中联考数学试题陕西省陕西师范大学附属中学2024-2025学年高二上学期期初考试数学试卷
名校
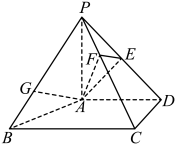
2 . 如图所示,有一个棱长为4的正四面体 容器,
容器, 是
是 的中点,
的中点, 是
是 上的动点,则下列说法正确的是( )
上的动点,则下列说法正确的是( )
 容器,
容器, 是
是 的中点,
的中点, 是
是 上的动点,则下列说法正确的是( )
上的动点,则下列说法正确的是( )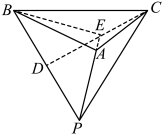
A.直线 与 与 所成的角为 所成的角为 |
B.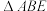 的周长最小值为 的周长最小值为 |
C.如果在这个容器中放入1个小球(全部进入),则小球半径的最大值为 |
D.如果在这个容器中放入4个完全相同的小球(全部进入),则小球半径的最大值为 |
您最近一年使用:0次
2023-09-01更新
|
4890次组卷
|
12卷引用:专题04 立体几何
(已下线)专题04 立体几何(已下线)第15题 立体几何中整体放入问题(压轴小题)安徽省六校教育研究会2024届高三上学期入学素质测试数学试题山西省山西大学附属中学2024届高三上学期9月月考(总第三次)数学试题安徽省合肥一六八中学等学校2024届高三上学期名校期末联合测试数学试题安徽“耀正优+”2024届高三名校上学期期末测试数学试题湖南省长沙市雅礼中学2024届高三一模数学试卷2024届河北省承德市部分高中二模数学试题河北省衡水市部分学校2024届高三下学期二模考试数学试题河南省信阳市新县高级中学2024届高三考前第三次适应性考试数学试题河北省重点高中2024届高三下学期5月模拟考试数学试题(二)安徽省2024届新高考预测数学模拟卷(四)
名校
3 . 如图,在四棱锥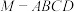 中,
中,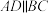 ,
,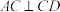 ,
,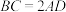 ,△MAD为等边三角形,平面
,△MAD为等边三角形,平面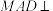 平面ABCD,点N在棱MD上,直线
平面ABCD,点N在棱MD上,直线 平面ACN.
平面ACN. .
.
(2)设二面角 的平面角为
的平面角为 ,直线CN与平面ABCD所成的角为
,直线CN与平面ABCD所成的角为 ,若
,若 的取值范围是
的取值范围是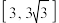 ,求
,求 的取值范围.
的取值范围.
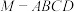 中,
中,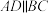 ,
,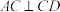 ,
,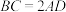 ,△MAD为等边三角形,平面
,△MAD为等边三角形,平面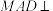 平面ABCD,点N在棱MD上,直线
平面ABCD,点N在棱MD上,直线 平面ACN.
平面ACN.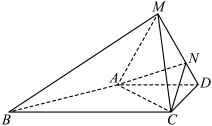
 .
.(2)设二面角
 的平面角为
的平面角为 ,直线CN与平面ABCD所成的角为
,直线CN与平面ABCD所成的角为 ,若
,若 的取值范围是
的取值范围是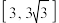 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2023-06-30更新
|
3663次组卷
|
8卷引用:第二章 立体几何中的计算 专题一 空间角 微点12 三正弦定理与三余弦定理(二)【培优版】
名校
解题方法
4 . 已知正四棱锥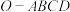 的底面边长为
的底面边长为 ,高为3.以点
,高为3.以点 为球心,
为球心, 为半径的球
为半径的球 与过点
与过点 的球
的球 相交,相交圆的面积为
相交,相交圆的面积为 ,则球
,则球 的半径为( )
的半径为( )
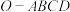 的底面边长为
的底面边长为 ,高为3.以点
,高为3.以点 为球心,
为球心, 为半径的球
为半径的球 与过点
与过点 的球
的球 相交,相交圆的面积为
相交,相交圆的面积为 ,则球
,则球 的半径为( )
的半径为( )A.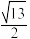 或 或 | B.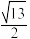 或 或 |
C. 或 或 | D. 或 或 |
您最近一年使用:0次
2023-03-26更新
|
3825次组卷
|
4卷引用:专题05 立体几何
名校
解题方法
5 . 如图,在四棱锥 中,平面
中,平面 平面
平面 ,
, ,
, ,
,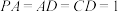 ,
, ,
,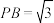 .
. 为
为 的中点,点
的中点,点 在
在 上,且
上,且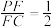 .
. 平面
平面 ;
;
(2)在棱 上是否存在点
上是否存在点 ,使得点
,使得点 到平面
到平面 的距离为
的距离为 ,若存在求出点
,若存在求出点 的位置,不存在请说明理由.
的位置,不存在请说明理由.
 中,平面
中,平面 平面
平面 ,
, ,
, ,
,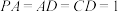 ,
, ,
,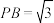 .
. 为
为 的中点,点
的中点,点 在
在 上,且
上,且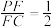 .
.
 平面
平面 ;
;(2)在棱
 上是否存在点
上是否存在点 ,使得点
,使得点 到平面
到平面 的距离为
的距离为 ,若存在求出点
,若存在求出点 的位置,不存在请说明理由.
的位置,不存在请说明理由.
您最近一年使用:0次
2023-07-18更新
|
3176次组卷
|
9卷引用:第11章 简单几何体(压轴必刷30题专项训练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(沪教版2020必修第三册)
(已下线)第11章 简单几何体(压轴必刷30题专项训练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(沪教版2020必修第三册)(已下线)第二章 立体几何中的计算 专题二 空间距离 微点3 点到平面的距离(二)【培优版】(已下线)高一下学期期末复习解答题压轴题二十四大题型专练(2)-举一反三系列(人教A版2019必修第二册)黑龙江省哈尔滨市第三中学校2022-2023学年高一下学期期末数学试题辽宁省本溪市高级中学2023-2024学年高三上学期高考适应性测试(一)数学试题辽宁省部分名校2023-2024学年高二上学期联考数学试题浙江省台州市温岭市新河中学2023-2024学年高一下学期6月阶段性考试数学试题山东省济宁市北大新世纪邹城实验学校2023-2024学年高一下学期期末考试数学试题福建省福州第八中学2024-2025学年高二上学期10月月考数学试题
名校
6 . 已知实数 ,则
,则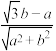 的取值范围是
的取值范围是______ .
 ,则
,则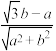 的取值范围是
的取值范围是
您最近一年使用:0次
2023-02-10更新
|
2704次组卷
|
15卷引用:2.3 直线的交点及距离公式(精练)-2023-2024学年高二数学《一隅三反》系列(人教A版2019选择性必修第一册)
(已下线)2.3 直线的交点及距离公式(精练)-2023-2024学年高二数学《一隅三反》系列(人教A版2019选择性必修第一册)(已下线)专题04 直线方程综合应用难题(12题型)-【巅峰课堂】2023-2024学年高二数学上学期期中期末复习讲练测(人教A版2019选择性必修第一册)(已下线)2.3.2 点到直线的距离公式、两条平行直线间的距离【第三课】(已下线)专题02 直线和圆的方程(1)(已下线)直线与方程(已下线)专题05 平面上的距离12种常见考法归类(1)浙江省绍兴市2022-2023学年高三上学期期末数学试题上海交通大学附属中学闵行分校2022-2023学年高二下学期3月月考数学试题上海市交通大学附属中学2022-2023学年高二下学期3月卓越考试数学试题浙江省杭州学军中学(紫金港校区)2022-2023学年高二下学期5月检测数学试题(已下线)高二上学期第一次月考填空题压轴题50题专练-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)(已下线)高二上学期期中考试填空题压轴题50题专练-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)浙江省杭州第二中学2023-2024学年高二下学期期中考试数学试题安徽省蚌埠市五河第一中学2024-2025学年高二上学期第二次月考检测数学试题陕西省师范大学附属中学2024-2025学年高二上学期期中考试数学试卷
名校
7 . 北京大兴国际机场的显著特点之一是各种弯曲空间的运用.刻画空间的弯曲性是几何研究的重要内容.用曲率刻画空间弯曲性,规定:多面体顶点的曲率等于 与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和.例如:正四面体在每个顶点有3个面角,每个面角是
与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和.例如:正四面体在每个顶点有3个面角,每个面角是 ,所以正四面体在各顶点的曲率为
,所以正四面体在各顶点的曲率为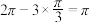 ,故其总曲率为
,故其总曲率为 .
.
(2)若多面体满足:顶点数-棱数+面数 ,证明:这类多面体的总曲率是常数.
,证明:这类多面体的总曲率是常数.
 与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和.例如:正四面体在每个顶点有3个面角,每个面角是
与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和.例如:正四面体在每个顶点有3个面角,每个面角是 ,所以正四面体在各顶点的曲率为
,所以正四面体在各顶点的曲率为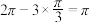 ,故其总曲率为
,故其总曲率为 .
.
(2)若多面体满足:顶点数-棱数+面数
 ,证明:这类多面体的总曲率是常数.
,证明:这类多面体的总曲率是常数.
您最近一年使用:0次
2021-01-23更新
|
9000次组卷
|
15卷引用:专题20 空间几何解答题(文科)-2
(已下线)专题20 空间几何解答题(文科)-2(已下线)专题19 空间几何解答题(理科)-2(已下线)第五篇 向量与几何 专题21 曲率与曲率圆 微点1 曲率与曲率圆(一)(已下线)重难点突破06 立体几何解答题最全归纳总结(九大题型)-3(已下线)立体几何新定义(已下线)专题15 立体几何解答题全归类(9大核心考点)(讲义)-2(已下线)11.1.2 构成空间几何体的基本元素-【帮课堂】(人教B版2019必修第四册)(已下线)专题4 立体几何中的新定义压轴大题(过关集训)(已下线)重组1 高二期中真题重组卷(河北卷)A基础卷2021年1月普通高等学校招生全国统一考试适应性测试(八省联考)数学试题(已下线)专题11.4《立体几何初步》(B卷提升篇)-2020-2021学年高一数学必修第四册同步单元AB卷(新教材人教B版)浙江省温州市永嘉中学2020-2021学年高一下学期期中数学试题(已下线)第8章 立体几何初步(压轴30题专练)-2021-2022学年高一数学考试满分全攻略(人教A版2019必修第二册)浙江省杭州学军中学2022-2023学年高二上学期期中模拟数学试题福建省福州外国语学校2023-2024学年高一下学期期中考试数学试卷
解题方法
8 . 已知正方体 的棱长为
的棱长为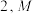 为空间中任一点,则下列结论中正确的是( )
为空间中任一点,则下列结论中正确的是( )
 的棱长为
的棱长为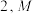 为空间中任一点,则下列结论中正确的是( )
为空间中任一点,则下列结论中正确的是( )A.若 为线段 为线段 上任一点,则 上任一点,则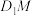 与 与 所成角的范围为 所成角的范围为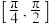 |
B.若 为正方形 为正方形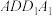 的中心,则三棱锥 的中心,则三棱锥 外接球的体积为 外接球的体积为 |
C.若 在正方形 在正方形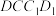 内部,且 内部,且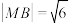 ,则点 ,则点 轨迹的长度为 轨迹的长度为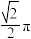 |
D.若三棱锥 的体积为 的体积为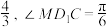 恒成立,点 恒成立,点 轨迹的为椭圆的一部分 轨迹的为椭圆的一部分 |
您最近一年使用:0次
2023-04-28更新
|
2865次组卷
|
6卷引用:模块九 第6套 1单选 2多选 2填空 2解答题(解析几何 导数)
(已下线)模块九 第6套 1单选 2多选 2填空 2解答题(解析几何 导数)(已下线)模块六 专题2 易错题目重组卷(山东卷)(已下线)第八章立体几何初步(单元测试)-【上好课】-(人教A版2019必修第二册)山东省济宁市2023届高三二模拟数学试题福建省福州市鼓山中学2023届高三适应性练习数学试题广东省阳江市2024届高三上学期开学适应性考试数学试题
名校
解题方法
9 . 底边和腰长之比为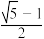 的等腰三角形被称为“黄金三角形”,四个面都为“黄金三角形”的四面体被称为“黄金四面体”.“黄金四面体”的外接球与内切球表面积之比为
的等腰三角形被称为“黄金三角形”,四个面都为“黄金三角形”的四面体被称为“黄金四面体”.“黄金四面体”的外接球与内切球表面积之比为______ .
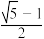 的等腰三角形被称为“黄金三角形”,四个面都为“黄金三角形”的四面体被称为“黄金四面体”.“黄金四面体”的外接球与内切球表面积之比为
的等腰三角形被称为“黄金三角形”,四个面都为“黄金三角形”的四面体被称为“黄金四面体”.“黄金四面体”的外接球与内切球表面积之比为
您最近一年使用:0次
2023-01-03更新
|
2724次组卷
|
7卷引用:“8+4+4”小题强化训练(20)
(已下线)“8+4+4”小题强化训练(20)(已下线)第八章立体几何初步章末题型大总结(精讲)(1)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)(已下线)专题7-1 立体几何压轴小题:截面与球(讲+练)-2(已下线)8.3.2 圆柱、圆锥、圆台、球的表面积和体积(2)-2022-2023学年高一数学《考点·题型·技巧》精讲与精练高分突破系列(人教A版2019必修第二册)(已下线)专题强化三 多面体与球有关的内切、外接问题-2022-2023学年高一数学《考点·题型·技巧》精讲与精练高分突破系列(苏教版2019必修第二册)(已下线)专题强化二 与球有关的内切、外接问题-2022-2023学年高一数学《考点·题型·技巧》精讲与精练高分突破系列(人教A版2019必修第二册)河北衡水中学2023届高三模拟数学试题
真题
名校
10 . 设三棱锥 的底面是正三角形,侧棱长均相等,
的底面是正三角形,侧棱长均相等, 是棱
是棱 上的点(不含端点),记直线
上的点(不含端点),记直线 与直线
与直线 所成角为
所成角为 ,直线
,直线 与平面
与平面 所成角为
所成角为 ,二面角
,二面角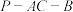 的平面角为
的平面角为 ,则
,则
 的底面是正三角形,侧棱长均相等,
的底面是正三角形,侧棱长均相等, 是棱
是棱 上的点(不含端点),记直线
上的点(不含端点),记直线 与直线
与直线 所成角为
所成角为 ,直线
,直线 与平面
与平面 所成角为
所成角为 ,二面角
,二面角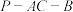 的平面角为
的平面角为 ,则
,则A.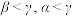 | B.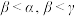 |
C.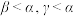 | D. |
您最近一年使用:0次
2019-06-09更新
|
14034次组卷
|
61卷引用:专题04 立体几何——2019年高考真题和模拟题理科数学分项汇编
(已下线)专题04 立体几何——2019年高考真题和模拟题理科数学分项汇编(已下线)专题04 立体几何——2019年高考真题和模拟题文科数学分项汇编(已下线)专题8.3 空间点、直线、平面之间的位置关系(练)-浙江版《2020年高考一轮复习讲练测》(已下线)狂刷39 立体几何的综合-学易试题君之小题狂刷2020年高考数学(理)(已下线)专题05 立体几何(选择题、填空题)——三年(2018-2020)高考真题文科数学分项汇编(已下线)专题05 立体几何(选择题、填空题)——三年(2018-2020)高考真题理科数学分项汇编(已下线)专题04 立体几何-五年(2016-2020)高考数学(文)真题分项(已下线)专题04 立体几何-五年(2016-2020)高考数学(理)真题分项(已下线)专题8.3 空间点、直线、平面之间的位置关系(练)-2021年新高考数学一轮复习讲练测(已下线)考点31 直线、平面垂直的判定及其性质-备战2021年高考数学(文)一轮复习考点一遍过(已下线)考点32 直线、平面垂直的判定及其性质-备战2021年高考数学(理)一轮复习考点一遍过(已下线)第32练 直线、平面垂直的判定与性质-2021年高考数学(理)一轮复习小题必刷(已下线)专题12 点线面的位置关系与空间的角-2021年浙江省高考数学命题规律大揭秘【学科网名师堂】(已下线)技巧01 选择题解法与技巧 第二篇 解题技巧篇(讲)-2021年高考数学二轮复习讲练测(浙江专用)(已下线)专题5.3 运用空间向量解决立体几何中的角与距离-备战2021年高考数学精选考点专项突破题集(新高考地区)(已下线)专题10 立体几何线面位置关系及空间角的计算 第一篇 热点、难点突破篇(讲)-2021年高考数学二轮复习讲练测(浙江专用)(已下线)押第12题立体几何-备战2021年高考数学临考题号押题(浙江专用)(已下线)考点30 空间线面位置关系的判定及其性质-备战2022年高考数学一轮复习考点帮(浙江专用)(已下线)考点32 直线、平面垂直的判定及其性质-备战2022年高考数学一轮复习考点帮(浙江专用)(已下线)考点21 直线、平面垂直的判定及其性质-备战2022年高考数学(文)一轮复习考点微专题(已下线)专题10 立体几何-五年(2017-2021)高考数学真题分项(新高考地区专用)(已下线)专题8.3 空间点、直线、平面之间的位置关系(练)- 2022年高考数学一轮复习讲练测(新教材新高考)(已下线)专题04 立体几何-五年(2017-2021)高考数学真题分项汇编(文科+理科)(已下线)考点33 直线与平面所成的角【理】-备战2022年高考数学典型试题解读与变式(已下线)专题10 立体几何线面位置关系及空间角的计算(讲)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(浙江专用)》(已下线)技巧01 选择题解法与技巧(讲)--第二篇 解题技巧篇-《2022年高考数学二轮复习讲练测(浙江专用)》(已下线)理科数学-2022年高考押题预测卷01(全国乙卷)(已下线)第09讲 空间点、直线、平面之间的关系(核心考点讲与练)-2021-2022学年高一数学考试满分全攻略(人教A版2019必修第二册)(已下线)第03讲 直线、平面平行垂直的判定与性质(练)(已下线)专题9 立体几何(已下线)重难点01 线线角、线面角、二面角问题(重难点突破解题技巧与方法)-2022-2023学年高二数学考试满分全攻略(沪教版2020必修第三册)(已下线)专题7 2022年高考“立体几何”专题命题分析(已下线)狂刷37 空间角与距离-学易试题君之小题狂刷2020年高考数学(理)(已下线)专题7-2 立体几何压轴小题:角度与动点、体积(讲+练)-1(已下线)专题18 空间几何题综合问题(体积、面积、角度、距离、轨迹等)(选填题)-3(已下线)第3章 空间向量及其应用(基础、常考、易错、压轴)分类专项训练(已下线)第五篇 向量与几何 专题17 三正弦定理、三余弦定理 微点1 三正弦定理、三余弦定理(已下线)重难点突破05 立体几何中的常考压轴小题(七大题型)-2(已下线)点线面之间的位置关系(已下线)通关练05 空间向量与立体几何近五年高考真题4考点精练(30题)- 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教A版2019选择性必修第一册)(已下线)专题14 立体几何选择题(理科)-2(已下线)专题13 立体几何选择题(文科)-2(已下线)拔高点突破03 立体几何中的常考压轴小题(七大题型)(已下线)专题24 2个二级结论速解二面角问题2019年浙江省高考数学试卷人教A版(2019) 必修第二册 逆袭之路 第八章 立体几何初步 专题五 高考中的直线、平面之间的位置关系人教A版(2019) 必修第二册 过关斩将 第八章 8.4~8.6 综合拔高练人教B版(2019) 必修第四册 过关斩将 第十一章 立体几何初步 11.3~11.4 综合拔高练人教A版(2019) 必修第二册 突围者 第八章 模拟高考检测2019年普通高等学校招生全国统一考试浙江卷(已下线)【新教材精创】1.2.4+二面角(2)A基础练-人教B版高中数学选择性必修第一册浙江省金华市曙光学校2020-2021学年高二下学期期中数学试题浙江省2021届高三高考数学预测卷(一)上海市曹杨二中2019-2020学年高二上学期期末数学试题河北省石家庄市十五中2021-2022学年高一下学期期中数学试题黑龙江省哈尔滨德强学校2021-2022学年高一下学期期末数学试题苏教版(2019) 必修第二册 过关斩将 第13章 13.2 综合拔高练沪教版(2020) 选修第一册 精准辅导 第3章 3.4(4)求角的大小(第2课时)沪教版(2020) 一轮复习 堂堂清 第八单元 8.4 平面与平面的位置关系辽宁省大连市滨城高中联盟2023-2024学年高二上学期10月月考数学试题辽宁省实验中学2023-2024学年高二上学期期中数学试题



