名校
解题方法
1 . 如图,在四棱锥 中,平面
中,平面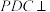 平面
平面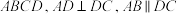 ,
,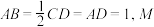 为棱
为棱 的中点.
的中点. 平面
平面 ;
;
(2)若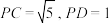 ,
,
(i)求二面角 的余弦值;
的余弦值;
(ii)在线段 上是否存在点Q,使得点Q到平面
上是否存在点Q,使得点Q到平面 的距离是
的距离是 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
 中,平面
中,平面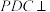 平面
平面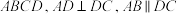 ,
,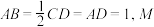 为棱
为棱 的中点.
的中点.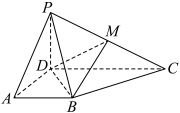
 平面
平面 ;
;(2)若
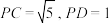 ,
,(i)求二面角
 的余弦值;
的余弦值;(ii)在线段
 上是否存在点Q,使得点Q到平面
上是否存在点Q,使得点Q到平面 的距离是
的距离是 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
您最近一年使用:0次
昨日更新
|
1855次组卷
|
20卷引用:江苏省盐城市五校联考2023-2024学年高二下学期第一次学情调研检测(3月)数学试题
江苏省盐城市五校联考2023-2024学年高二下学期第一次学情调研检测(3月)数学试题湖南省常德市汉寿县第一中学2023-2024学年高二下学期3月月考数学试题上海市格致中学2023-2024学年高二下学期期中考试数学试题福建省莆田第二十五中学2023-2024学年高二下学期期中考试数学试题(已下线)专题03 空间向量及其应用全章复习攻略--高二期末考点大串讲(沪教版2020选修)(已下线)专题02 空间向量与立体几何--高二期末考点大串讲(苏教版2019选择性必修第二册)(已下线)专题03空间向量及其应用--高二期末考点大串讲(沪教版2020选修)(已下线)第06讲 空间向量的应用(二)-【暑假预科讲义】(人教A版2019选择性必修第一册)宁夏银川市第九中学2023-2024学年高一下学期期末考试数学试卷黑龙江省哈尔滨市第六中学校2023-2024学年高一下学期期末测试数学试题山东省泰安市肥城市慈明学校2023-2024学年高一下学期期末检测数学试卷福建省三明第一中学2024-2025学年高二上学期8月月考数学试题(已下线)专题5 空间向量求值及范围问题【练】(高二期中压轴专项)福建省泉州市晋江市侨声中学2024-2025学年高二上学期教学质量监测(一)数学试卷福建省莆田第十中学2024-2025学年高二上学期10月月考数学试卷内蒙古自治区通辽市第一中学2024-2025学年高二上学期10月月考数学试题河北省石家庄精英未来高级中学2024-2025学年高二上学期第一次月考数学试题山东省新泰市紫光实验中学2024-2025学年高二上学期开学考试数学试题山东省济宁市嘉祥县第一中学2024-2025学年高二上学期第一次月考数学试题河北省邯郸市武安市第一中学2024-2025学年高二上学期10月期中考试数学试题
2 . 如图,在四棱锥 中,侧棱
中,侧棱 底面
底面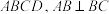 ,且
,且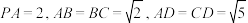 .
. 平面
平面 ;
;
(2)求平面 与平面
与平面 夹角的正弦值.
夹角的正弦值.
 中,侧棱
中,侧棱 底面
底面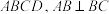 ,且
,且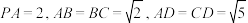 .
.
 平面
平面 ;
;(2)求平面
 与平面
与平面 夹角的正弦值.
夹角的正弦值.
您最近一年使用:0次
7日内更新
|
364次组卷
|
2卷引用:山东省齐鲁名校联盟·天一大联考2024-2025学年高三上学期第二次联考(10月)数学试题
名校
3 . 设等比数列 的前
的前 项和为
项和为 ,则“数列
,则“数列 为递增数列”是“
为递增数列”是“ ”的( )
”的( )
 的前
的前 项和为
项和为 ,则“数列
,则“数列 为递增数列”是“
为递增数列”是“ ”的( )
”的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
您最近一年使用:0次
7日内更新
|
609次组卷
|
3卷引用:山东省齐鲁名校联盟·天一大联考2024-2025学年高三上学期第二次联考(10月)数学试题
解题方法
4 . 过双曲线 的左焦点
的左焦点 作直线与它的两条渐近线分别交于
作直线与它的两条渐近线分别交于 两点,且
两点,且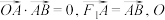 是坐标原点,则双曲线的离心率是( )
是坐标原点,则双曲线的离心率是( )
 的左焦点
的左焦点 作直线与它的两条渐近线分别交于
作直线与它的两条渐近线分别交于 两点,且
两点,且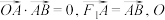 是坐标原点,则双曲线的离心率是( )
是坐标原点,则双曲线的离心率是( )| A.2 | B. | C. | D.3 |
您最近一年使用:0次
7日内更新
|
566次组卷
|
2卷引用:河南省南阳市六校2024-2025学年高二上学期第一次联考(10月)数学试题
名校
5 . 已知双曲线 的左焦点为
的左焦点为 ,
, 为坐标原点,若在
为坐标原点,若在 的右支上存在关于
的右支上存在关于 轴对称的两点
轴对称的两点 ,使得
,使得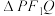 为正三角形,且
为正三角形,且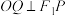 ,则
,则 的离心率为( )
的离心率为( )
 的左焦点为
的左焦点为 ,
, 为坐标原点,若在
为坐标原点,若在 的右支上存在关于
的右支上存在关于 轴对称的两点
轴对称的两点 ,使得
,使得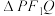 为正三角形,且
为正三角形,且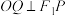 ,则
,则 的离心率为( )
的离心率为( )A. | B.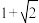 | C. | D. |
您最近一年使用:0次
7日内更新
|
1725次组卷
|
4卷引用:浙江省浙南名校联盟2024-2025学年高三上学期第一次联考(10月)数学试题
浙江省浙南名校联盟2024-2025学年高三上学期第一次联考(10月)数学试题(已下线)2.6.2 双曲线的几何性质——课后作业(提升版)四川省成都市树德中学2024-2025学年高三上学期数学综合测试四山东省新泰市弘文中学2025届高三上学期开学考试数学试题
名校
6 . (1)已知集合 ,若“
,若“ ”是“
”是“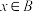 ”的充分不必要条件,求实数
”的充分不必要条件,求实数 的取值范围.
的取值范围.
(2)命题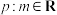 且
且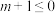 ,命题
,命题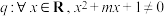 ,若
,若 与
与 不同时为真命题,求
不同时为真命题,求 的取值范围.
的取值范围.
 ,若“
,若“ ”是“
”是“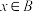 ”的充分不必要条件,求实数
”的充分不必要条件,求实数 的取值范围.
的取值范围.(2)命题
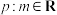 且
且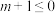 ,命题
,命题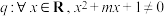 ,若
,若 与
与 不同时为真命题,求
不同时为真命题,求 的取值范围.
的取值范围.
您最近一年使用:0次
7日内更新
|
809次组卷
|
8卷引用:湖北省新高考联考协作体2024-2025学年高一上学期9月月考数学试题
湖北省新高考联考协作体2024-2025学年高一上学期9月月考数学试题江苏省扬州市扬州中学2024-2025学年高一上学期10月自主学习评估数学试题广西壮族自治区南宁市青秀区南宁沛鸿民族中学2024-2025学年高一上学期10月月考数学试题福建省安溪第八中学2024-2025学年高一上学期第一次质量检测数学试题内蒙古赤峰市赤峰二中2024-2025学年高一上学期第一次月考数学试题河南省驻马店市新蔡县第一高级中学2024-2025学年高一上学期10月月考数学试题湖北省武汉市武钢三中2024-2025学年高一上学期10月月考数学试题山东省新泰市紫光实验中学2024-2025学年高一上学期开学考试数学试题
7 . 已知椭圆 的右焦点为
的右焦点为 ,斜率不为0的直线
,斜率不为0的直线 与
与 交于
交于 两点.
两点.
(1)若 是线段
是线段 的中点,求直线
的中点,求直线 的方程;
的方程;
(2)若直线 经过点
经过点 (点
(点 在点
在点 之间),直线
之间),直线 与直线
与直线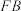 的斜率分别为
的斜率分别为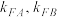 ,求证:
,求证: 为定值.
为定值.
 的右焦点为
的右焦点为 ,斜率不为0的直线
,斜率不为0的直线 与
与 交于
交于 两点.
两点.(1)若
 是线段
是线段 的中点,求直线
的中点,求直线 的方程;
的方程;(2)若直线
 经过点
经过点 (点
(点 在点
在点 之间),直线
之间),直线 与直线
与直线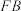 的斜率分别为
的斜率分别为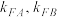 ,求证:
,求证: 为定值.
为定值.
您最近一年使用:0次
7日内更新
|
1332次组卷
|
3卷引用:江苏省南通市海安市实验中学2024-2025学年高二上学期第一次学情检测(10月)数学试题
名校
8 . 如图,正方体 的棱长为1,
的棱长为1, 分别是棱
分别是棱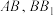 的中点,点P在对角线
的中点,点P在对角线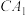 上运动,则
上运动,则 的面积的最小值为
的面积的最小值为______ .
 的棱长为1,
的棱长为1, 分别是棱
分别是棱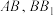 的中点,点P在对角线
的中点,点P在对角线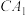 上运动,则
上运动,则 的面积的最小值为
的面积的最小值为
您最近一年使用:0次
名校
解题方法
9 . 在①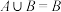 ;②“
;②“ ”是“
”是“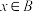 ”的充分不必要条件;③
”的充分不必要条件;③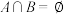 ,这三个条件中任选一个,补充到下面的问题中,并解答.
,这三个条件中任选一个,补充到下面的问题中,并解答.
问题:已知集合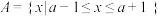 ,
,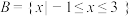 .
.
(1)当 时,求
时,求 ;
;
(2)若______,求实数 的取值范围.
的取值范围.
注:如果选择多个条件分别解答,按第一个解答计分.
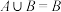 ;②“
;②“ ”是“
”是“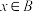 ”的充分不必要条件;③
”的充分不必要条件;③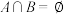 ,这三个条件中任选一个,补充到下面的问题中,并解答.
,这三个条件中任选一个,补充到下面的问题中,并解答.问题:已知集合
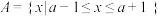 ,
,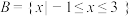 .
.(1)当
 时,求
时,求 ;
;(2)若______,求实数
 的取值范围.
的取值范围.注:如果选择多个条件分别解答,按第一个解答计分.
您最近一年使用:0次
2024-10-21更新
|
348次组卷
|
47卷引用:山东省济宁市2020-2021学年高一上学期期末数学试题
山东省济宁市2020-2021学年高一上学期期末数学试题浙江省湖州市德清县第三中学2020-2021学年高一下学期返校考试数学试题江苏省吴江中学明伦书院创新班2020-2021学年高一下学期期中数学试题(已下线)专题2.1 充分条件、必要条件、充要条件-重难点题型精讲-2021-2022学年高一数学举一反三系列(苏教版2019必修第一册)(已下线)专题1.7 充分条件与必要条件-重难点题型精讲-2021-2022学年高一数学举一反三系列(人教A版2019必修第一册)(已下线)第一章 (基础过关)集合与常用逻辑用语 A卷-【双基双测】2021-2022学年高一数学同步AB卷(浙江专用)(人教A版2019必修第一册)(已下线)专题01 充分条件与必要条件-2021-2022学年高一《新题速递·数学》(人教A版2019)山西省实验中学2021-2022学年高一上学期第一次月考数学试题(已下线)专题1.7 必要条件与充分条件-重难点题型精讲-2021-2022学年高一数学举一反三系列(北师大版2019必修第一册)(已下线)专题1.9 充分条件、必要条件-重难点题型精讲-2021-2022学年高一数学举一反三系列(人教B版2019必修第一册)湖北省武汉中学2021-2022学年高一上学期第一次月考数学试题辽宁省辽东南协作体2021-2022学年高一上学期第一次月考数学试题江苏省南通市如皋市第一中学2021-2022学年高一上学期10月月考数学试题广东省广州市培英中学2021-2022学年高一上学期10月月考数学试题安徽省阜阳市第一中学2021-2022学年高一上学期第一次月考数学试题江苏省盐城市阜宁中学2021-2022学年高一上学期第一次月考数学试题海南省海口市第一中学2020-2021学年高一9月质量检测数学试题重庆市杨家坪中学2021-2022学年高一上学期第一次月考数学试题 河北省石家庄市四十四中2021-2022学年高一上学期第一次月考(10月)数学试题湖南省邵阳市武冈市第二中学2021-2022学年高一上学期10月月考数学试题江苏省盐城市伍佑中学2021-2022学年高一上学期学情调研(一)数学试题吉林省白城市第一中学2021-2022学年高一上学期期中数学试题江苏省连云港市赣榆第一中学2021-2022学年高一上学期10月月考数学试题甘肃省兰州市第五十九中学2021-2022学年高一上学期期中数学试题(已下线)第一章 集合与常用逻辑用语章末测试(章末测试)-【上好课】2021-2022学年高一数学同步备课系列(人教A版2019必修第一册)河北省博野中学2021-2022学年高一上学期10月月考数学试题湖南省邵阳市新邵县2021-2022学年高一上学期期末质量检测数学试题云南省昆明市第十中学2021-2022学年高一上学期第二次阶段考试数学试题第2章 常用逻辑用语 单元综合检测(难点)(已下线)突破1.4充分条件与必要条件(重难点突破)2023版 湘教版(2019) 必修第一册 过关斩将 第1章 综合拔高练江苏省南通市如皋中学2022-2023学年高一上学期质量检测(一)数学试题四川省南充市营山县营山中学校2022-2023学年高一上学期10月月考数学试题四川省成都市成都市第七中学2022-2023学年高一上学期10月月考数学试题江苏省徐州市沛县2022-2023学年高一上学期第一次学情调研数学试题浙江省金华市东阳市横店高中2022-2023学年高一上学期10月检测数学试题河北省高碑店市崇德实验中学2022-2023学年高一上学期9月月考数学试题河北省承德市双滦区实验中学2022-2023学年高一上学期期中数学试题安徽省合肥市庐江第五中学2022-2023学年高一上学期期中数学试题山东省淄博第五中学2022-2023学年高一下学期3月月考数学试题云南省腾冲市2022-2023学年高一上学期期中教育教学质量监测数学试卷云南省保山市腾冲市第八中学2022-2023学年高一上学期期中数学试题江西省南昌市知行中学2022-2023学年高一上学期10月月考数学试题江西省赣州市赣州中学2024-2025学年高一上学期第一次月考数学试题江苏省木渎高级中学2024-2025学年高一上学期十月调研测试数学试题江苏省苏州实验中学2024-2025学年高一上学期10月月考数学试题江苏省昆山市陆家中学2024-2025学年高一上学期10月月考数学试题
10 . 已知抛物线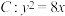 的焦点为
的焦点为 ,准线为
,准线为 ,点
,点 在
在 上,点
上,点 在
在 上.若
上.若 ,
,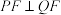 ,则
,则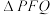 的面积为( )
的面积为( )
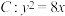 的焦点为
的焦点为 ,准线为
,准线为 ,点
,点 在
在 上,点
上,点 在
在 上.若
上.若 ,
,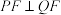 ,则
,则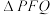 的面积为( )
的面积为( )A.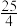 | B.25 | C.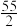 | D.55 |
您最近一年使用:0次



