名校
解题方法
1 . 已知椭圆 的左、右焦点分别为
的左、右焦点分别为 、
、 ,经过
,经过 的直线交椭圆于
的直线交椭圆于 ,
, ,
, 的内切圆的圆心为
的内切圆的圆心为 ,若
,若 ,则该椭圆的离心率是( )
,则该椭圆的离心率是( )
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,经过
,经过 的直线交椭圆于
的直线交椭圆于 ,
, ,
, 的内切圆的圆心为
的内切圆的圆心为 ,若
,若 ,则该椭圆的离心率是( )
,则该椭圆的离心率是( )A.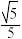 | B. | C. | D. |
您最近一年使用:0次
2022-05-27更新
|
11166次组卷
|
28卷引用:江苏省盐城市第一中学2022-2023学年高二上学期第二次学情调研考试数学试题
江苏省盐城市第一中学2022-2023学年高二上学期第二次学情调研考试数学试题陕西省西北工业大学附属中学2022届高三下学期第十三次适应性训练理科数学试题(已下线)考点8-2 椭圆及其性质(文理)浙江省名校协作体2022-2023学年高三上学期适应性联合考试数学试题(已下线)专题15 圆锥曲线焦点三角形 微点3 圆锥曲线焦点三角形内切圆问题湖南省长沙市长郡中学2022-2023学年高二上学期第一次月考数学试题(已下线)专题38 椭圆及其性质-4四川省树德中学(宁夏街校区)2022-2023学年高三上学期10月阶段性测试数学(文)试题(已下线)专题28 轻松搞定圆锥曲线离心率十九大模型-2(已下线)专题9-3 求椭圆双曲线离心率题型归类-2江西省上饶市第四中学2022-2023学年高二上学期第三次月考数学试题山东省枣庄市滕州市2022-2023学年高二上学期期末数学试题(已下线)第14讲 椭圆离心率6种常考题型四川省蓬溪中学校2022-2023学年高二下学期第二次质量检测数学(理)试题四川省蓬溪中学校2022-2023学年高二下学期第二次质量检测数学(文)试题黑龙江省哈尔滨市兆麟中学2023-2024学年高二上学期期中考试数学试题(已下线)四川省成都市第七中学2023-2024学年高二上学期12月月考数学试题新疆维吾尔自治区阿克苏地库车市第二中学2023-2024学年高二上学期第二次月考(12月)数学广东省广州市广东实验中学2024届高三上学期第二次调研数学试题(已下线)圆锥 曲线2024届高三新改革适应性模拟训练数学试卷七(九省联考题型)山东省青岛第二中学2023-2024学年高二下学期3月月考数学试卷辽宁省名校联盟2023-2024学年高二下学期4月联合考试数学试卷浙江省宁波市鄞州中学2023-2024学年高二上学期期中考试数学试题浙江省杭州第二中学2023-2024学年高二下学期期中考试数学试题浙江省宁波市鄞州中学2023-2024学年高二上学期9月月考数学试题专题07椭圆问题(选择填空题)安徽省蚌埠市五河第一中学2024-2025学年高二上学期期中考试数学试题
名校
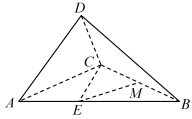
2 . 如图,在三棱锥 中,
中, ,
, ,记二面角
,记二面角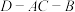 的平面角为
的平面角为 .
.
(1)若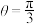 ,
, ,求三棱锥
,求三棱锥 的体积;
的体积;
(2)若M为BC的中点,求直线AD与EM所成角的取值范围.
 中,
中, ,
, ,记二面角
,记二面角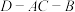 的平面角为
的平面角为 .
.
(1)若
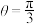 ,
, ,求三棱锥
,求三棱锥 的体积;
的体积;(2)若M为BC的中点,求直线AD与EM所成角的取值范围.
您最近一年使用:0次
2022-01-24更新
|
4998次组卷
|
10卷引用:江苏省盐城市五校联考2022-2023学年高二下学期5月阶段性测试数学试题
江苏省盐城市五校联考2022-2023学年高二下学期5月阶段性测试数学试题广东省佛山市2021-2022学年高二上学期期末数学试题浙江省金华十校2021-2022学年高一下学期期末模拟数学试题吉林省东北师范大学附属中学2022-2023学年高二上学期第一次月考数学试题江西省上饶市广丰区重点高中2022-2023学年高二上学期第三次月考数学试题湖北省襄阳市第五中学2023-2024学年高二上学期新起点考试数学试题(已下线)高二数学上学期期中模拟卷02(原卷版)(已下线)难关必刷01 空间向量的综合应用-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(人教A版2019选择性必修第一册)(已下线)第一章 空间向量与立体几何(压轴题专练,精选20题)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第一册)(已下线)专题08 空间向量基底法在立体几何问题中的应用4种常见考法归类 - 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教A版2019选择性必修第一册)
名校
解题方法
3 . 在平面直角坐标系 中,已知椭圆
中,已知椭圆 的长轴为4,过坐标原点的直线交
的长轴为4,过坐标原点的直线交 于
于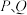 两点,若
两点,若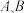 分别为椭圆
分别为椭圆 的左、右顶点,且直线
的左、右顶点,且直线 与直线
与直线 的斜率之积为
的斜率之积为 .
.
(1)求椭圆的标准方程;
(2)若点 在第一象限,
在第一象限, 轴,垂足为
轴,垂足为 ,连
,连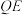 并延长交
并延长交 于点
于点 ,
,
(i)证明: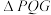 为直角三角形;
为直角三角形;
(ii)若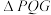 的面积为
的面积为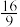 ,求直线
,求直线 的斜率.
的斜率.
 中,已知椭圆
中,已知椭圆 的长轴为4,过坐标原点的直线交
的长轴为4,过坐标原点的直线交 于
于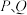 两点,若
两点,若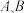 分别为椭圆
分别为椭圆 的左、右顶点,且直线
的左、右顶点,且直线 与直线
与直线 的斜率之积为
的斜率之积为 .
.(1)求椭圆的标准方程;
(2)若点
 在第一象限,
在第一象限, 轴,垂足为
轴,垂足为 ,连
,连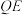 并延长交
并延长交 于点
于点 ,
,(i)证明:
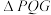 为直角三角形;
为直角三角形;(ii)若
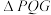 的面积为
的面积为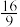 ,求直线
,求直线 的斜率.
的斜率.
您最近一年使用:0次
2023-05-28更新
|
1110次组卷
|
2卷引用:江苏省建湖高级中学2023-2024学年高二下学期期初测试(2月)数学试题
名校
解题方法
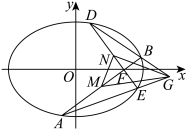
4 . 已知椭圆C: ,过右焦点F的直线l交C于A,B两点,过点F与l垂直的直线交C于D,E两点,其中B,D在x轴上方,M,N分别为AB,DE的中点.当
,过右焦点F的直线l交C于A,B两点,过点F与l垂直的直线交C于D,E两点,其中B,D在x轴上方,M,N分别为AB,DE的中点.当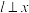 轴时,
轴时,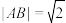 ,椭圆C的离心率为
,椭圆C的离心率为 .
.
(2)证明:直线MN过定点,并求定点坐标;
(3)设G为直线AE与直线BD的交点,求△GMN面积的最小值.
 ,过右焦点F的直线l交C于A,B两点,过点F与l垂直的直线交C于D,E两点,其中B,D在x轴上方,M,N分别为AB,DE的中点.当
,过右焦点F的直线l交C于A,B两点,过点F与l垂直的直线交C于D,E两点,其中B,D在x轴上方,M,N分别为AB,DE的中点.当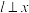 轴时,
轴时,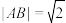 ,椭圆C的离心率为
,椭圆C的离心率为 .
.
(2)证明:直线MN过定点,并求定点坐标;
(3)设G为直线AE与直线BD的交点,求△GMN面积的最小值.
您最近一年使用:0次
2024-06-11更新
|
832次组卷
|
5卷引用:江苏省盐城市五校联盟2023-2024学年高二下学期第七次考试(5月)数学试题
江苏省盐城市五校联盟2023-2024学年高二下学期第七次考试(5月)数学试题浙江省丽水市五校高中发展共同体2023-2024学年高二下学期5月期中考试数学试题江苏省前黄高级中学2024届高三下学期三模适应性考试数学试题(已下线)专题7 圆锥曲线硬解定理【练】(已下线)专题14 圆锥曲线中的蝴蝶模型(高三压轴题)【练】
名校
解题方法
5 . 已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
, 是椭圆上任意一点,直线
是椭圆上任意一点,直线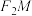 垂直于
垂直于 且交线段
且交线段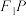 于点
于点 ,若
,若 ,则该椭圆的离心率的取值范围是
,则该椭圆的离心率的取值范围是______ .
 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
, 是椭圆上任意一点,直线
是椭圆上任意一点,直线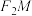 垂直于
垂直于 且交线段
且交线段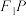 于点
于点 ,若
,若 ,则该椭圆的离心率的取值范围是
,则该椭圆的离心率的取值范围是
您最近一年使用:0次
2020-04-10更新
|
3719次组卷
|
10卷引用:江苏省盐城市伍佑中学2021-2022学年高二上学期期中数学试题
江苏省盐城市伍佑中学2021-2022学年高二上学期期中数学试题2019届浙江省绍兴市柯桥区高三上学期期末数学试题河南省许昌高级中学2020-2021学年第一学期第二次调研考试高二数学文科试题浙江省宁波市北仑中学2021-2022学年高二上学期期中数学试题(已下线)3.1 椭圆吉林省长春市第二实验中学2022-2023学年高二上学期第一次月考数学试题(已下线)专题9-3 求椭圆双曲线离心率题型归类-3吉林省长春市实验中学2022-2023学年高二上学期期中数学试题(已下线)专题22 圆锥曲线的离心率问题-3(已下线)专题7-3圆锥曲线离心率归类-2
名校
6 . 在平面直角坐标系 中,已知
中,已知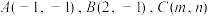 为三个不同的定点,且A,B,C不共线,.以原点
为三个不同的定点,且A,B,C不共线,.以原点 为圆心的圆与线段
为圆心的圆与线段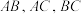 都相切.
都相切.
(Ⅰ)求圆 的方程及
的方程及 的值;
的值;
(Ⅱ)若直线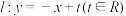 与圆
与圆 相交于
相交于 两点,且
两点,且 ,求
,求 的值;
的值;
(Ⅲ)在直线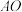 上是否存在异于
上是否存在异于 的定点
的定点 ,使得对圆
,使得对圆 上任意一点
上任意一点 ,都有
,都有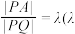 为常数
为常数 ?若存在,求出点
?若存在,求出点 的坐标及
的坐标及 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 中,已知
中,已知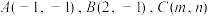 为三个不同的定点,且A,B,C不共线,.以原点
为三个不同的定点,且A,B,C不共线,.以原点 为圆心的圆与线段
为圆心的圆与线段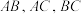 都相切.
都相切.(Ⅰ)求圆
 的方程及
的方程及 的值;
的值;(Ⅱ)若直线
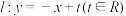 与圆
与圆 相交于
相交于 两点,且
两点,且 ,求
,求 的值;
的值;(Ⅲ)在直线
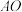 上是否存在异于
上是否存在异于 的定点
的定点 ,使得对圆
,使得对圆 上任意一点
上任意一点 ,都有
,都有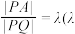 为常数
为常数 ?若存在,求出点
?若存在,求出点 的坐标及
的坐标及 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
2019-07-08更新
|
3663次组卷
|
11卷引用:江苏省盐城市响水中学2019-2020学年高一下学期学情分析考试(二)数学试题
江苏省盐城市响水中学2019-2020学年高一下学期学情分析考试(二)数学试题北京市朝阳区2018-2019学年高一下学期期末数学试题上海交通大学附属中学2019-2020学年高二上学期期中数学试题安徽省卓越县中联盟2020-2021学年高二上学期期中联考数学(理)试题上海市金山中学2021届高三上学期期中数学试题黑龙江省哈尔滨市第三中学2021-2022学年高二上学期10月月考数学(普通班)试题(已下线)2.4 圆的方程-2021-2022学年高二数学尖子生同步培优题典(人教A版2019选择性必修第一册)广东省佛山市南海区南海执信中学2021-2022学年高二上学期第二次段测数学试题吉林省长春市东北师范大学附属中学2021-2022学年高二上学期10月阶段考试数学(理)试题第二章 直线与圆的方程单元测试(巅峰版)-【新教材优创】突破满分数学之2022-2023学年高二数学重难点突破+课时训练 (人教A版2019选择性必修第一册)山东省德州市夏津县第一中学2023-2024学年高二上学期10月月考数学试题
名校
解题方法
7 . 已知抛物线 :
: 的焦点
的焦点 到其准线的距离为
到其准线的距离为 ,椭圆
,椭圆 :
: 经过抛物线
经过抛物线 的焦点
的焦点 .
.
(1)椭圆 的离心率
的离心率 ,求椭圆短轴的取值范围;
,求椭圆短轴的取值范围;
(2)已知 为坐标原点,过点
为坐标原点,过点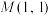 的直线
的直线 与椭圆
与椭圆 相交于
相交于 ,
, 两点.若
两点.若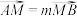 ,点
,点 满足
满足 ,且
,且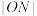 的最小值为
的最小值为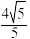 ,求椭圆
,求椭圆 的离心率.
的离心率.
 :
: 的焦点
的焦点 到其准线的距离为
到其准线的距离为 ,椭圆
,椭圆 :
: 经过抛物线
经过抛物线 的焦点
的焦点 .
.(1)椭圆
 的离心率
的离心率 ,求椭圆短轴的取值范围;
,求椭圆短轴的取值范围;(2)已知
 为坐标原点,过点
为坐标原点,过点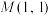 的直线
的直线 与椭圆
与椭圆 相交于
相交于 ,
, 两点.若
两点.若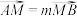 ,点
,点 满足
满足 ,且
,且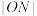 的最小值为
的最小值为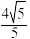 ,求椭圆
,求椭圆 的离心率.
的离心率.
您最近一年使用:0次
名校
解题方法
8 . 已知椭圆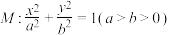 经过
经过 和
和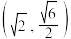 ,
,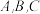 分别为椭圆的左顶点、右顶点、上顶点.
分别为椭圆的左顶点、右顶点、上顶点.
(1)求椭圆 的标准方程;
的标准方程;
(2)过 轴上点
轴上点 (点
(点 在椭圆
在椭圆 长轴上)作直线交椭圆
长轴上)作直线交椭圆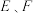 两点,且
两点,且 ,若
,若 ,求
,求 点的坐标;
点的坐标;
(3)过点 作直线交椭圆
作直线交椭圆 于
于 点,交直线
点,交直线 于
于 ,直线
,直线 于
于 轴相交于
轴相交于 ,求证:
,求证: 为定值,并求此定值.(其中
为定值,并求此定值.(其中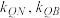 分别为直线
分别为直线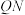 和直线l,
和直线l,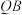 的斜率).
的斜率).
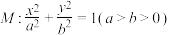 经过
经过 和
和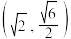 ,
, 分别为椭圆的左顶点、右顶点、上顶点.
分别为椭圆的左顶点、右顶点、上顶点.(1)求椭圆
 的标准方程;
的标准方程;(2)过
 轴上点
轴上点 (点
(点 在椭圆
在椭圆 长轴上)作直线交椭圆
长轴上)作直线交椭圆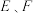 两点,且
两点,且 ,若
,若 ,求
,求 点的坐标;
点的坐标;(3)过点
 作直线交椭圆
作直线交椭圆 于
于 点,交直线
点,交直线 于
于 ,直线
,直线 于
于 轴相交于
轴相交于 ,求证:
,求证: 为定值,并求此定值.(其中
为定值,并求此定值.(其中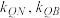 分别为直线
分别为直线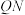 和直线l,
和直线l,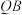 的斜率).
的斜率).
您最近一年使用:0次
名校
解题方法
9 . 已知椭圆 的两个焦点坐标分别是(-2,0),(2,0),并且经过点
的两个焦点坐标分别是(-2,0),(2,0),并且经过点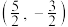 ,
, ,
, 是椭圆
是椭圆 上的不同两点,且以
上的不同两点,且以 为直径的圆经过原点
为直径的圆经过原点 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)是否存在圆心在原点的圆恒与直线 相切,若存在,求出该圆的方程,若不存在,说明理由;
相切,若存在,求出该圆的方程,若不存在,说明理由;
(3)求 的最小值.
的最小值.
 的两个焦点坐标分别是(-2,0),(2,0),并且经过点
的两个焦点坐标分别是(-2,0),(2,0),并且经过点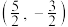 ,
, ,
, 是椭圆
是椭圆 上的不同两点,且以
上的不同两点,且以 为直径的圆经过原点
为直径的圆经过原点 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)是否存在圆心在原点的圆恒与直线
 相切,若存在,求出该圆的方程,若不存在,说明理由;
相切,若存在,求出该圆的方程,若不存在,说明理由;(3)求
 的最小值.
的最小值.
您最近一年使用:0次
2020-10-22更新
|
1392次组卷
|
3卷引用:江苏省盐城市2021-2022学年高三上学期第二次大联考数学试题
名校
10 . 已知椭圆 :
: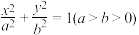 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线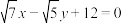 相切.
相切.
(1)求椭圆 的方程;
的方程;
(2)设 ,过点
,过点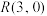 作与
作与 轴不重合的直线
轴不重合的直线 交椭圆
交椭圆 于
于 ,
, 两点,连接
两点,连接 ,
, 分别交直线
分别交直线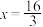 于
于 ,
, 两点,若直线
两点,若直线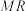 、
、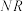 的斜率分别为
的斜率分别为 、
、 ,试问:
,试问: 是否为定值?若是,求出该定值,若不是,请说明理由.
是否为定值?若是,求出该定值,若不是,请说明理由.
 :
: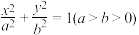 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线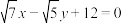 相切.
相切.(1)求椭圆
 的方程;
的方程;(2)设
 ,过点
,过点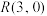 作与
作与 轴不重合的直线
轴不重合的直线 交椭圆
交椭圆 于
于 ,
, 两点,连接
两点,连接 ,
, 分别交直线
分别交直线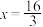 于
于 ,
, 两点,若直线
两点,若直线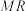 、
、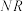 的斜率分别为
的斜率分别为 、
、 ,试问:
,试问: 是否为定值?若是,求出该定值,若不是,请说明理由.
是否为定值?若是,求出该定值,若不是,请说明理由.
您最近一年使用:0次
2016-12-04更新
|
2861次组卷
|
13卷引用:江苏省盐城市阜宁中学2021-2022学年高二上学期第一次阶段检测数学试题
江苏省盐城市阜宁中学2021-2022学年高二上学期第一次阶段检测数学试题2016届重庆市巴蜀中学高三上学期第三次月考理科数学试卷2016届安徽省六安一中高三下学期综合训练一理科数学试卷2016届黑龙江哈尔滨六中高三下四模考试文科数学试卷2019年四川省仁寿一中等西南四省八校高三9月份联考数学(文)试题四川省仁寿一中等西南四省八校2020届高三9月份联考数学(理)试题重庆市江津中学、实验中学等七校2020届高三下学期6月联考(三诊)数学(文)试题湖北省武汉襄阳荆门宜昌四地六校考试联盟2020-2021学年高三上学期起点联考数学试题广东省深圳市菁华学校2020-2021学年高二上学期12月月考数学试题湖北省华中师大一附中等六校2020-2021学年高三上学期联考数学试题(已下线)第64讲 章末检测九(已下线)专题32 一类与斜率和、差、商、积问题的探究-2海南省文昌市文昌中学、华迈实验中学2023-2024学年高二上学期期中段考数学试题



