名校
解题方法
1 . 已知椭圆 的离心率为
的离心率为 ,上顶点为
,上顶点为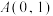 .
.
(1)求椭圆 的方程;
的方程;
(2)过点 且斜率为
且斜率为 的直线与椭圆
的直线与椭圆 交于不同的两点
交于不同的两点 ,
, ,且
,且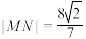 ,求
,求 的值.
的值.
 的离心率为
的离心率为 ,上顶点为
,上顶点为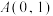 .
.(1)求椭圆
 的方程;
的方程;(2)过点
 且斜率为
且斜率为 的直线与椭圆
的直线与椭圆 交于不同的两点
交于不同的两点 ,
, ,且
,且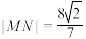 ,求
,求 的值.
的值.
您最近一年使用:0次
2022-03-05更新
|
3908次组卷
|
18卷引用:天津市军粮城中学2022-2023学年高三上学期期中数学试题
天津市军粮城中学2022-2023学年高三上学期期中数学试题天津市天津中学2022-2023学年高二上学期期中数学试题天津市武清区南蔡村中学2023-2024学年高二上学期第二次月考数学试题江苏省镇江市丹阳高级中学2021-2022学年高二(1-16,20班)下学期期初考试数学试题重庆市西南大学附属中学校2021-2022学年高二(广延班)下学期第三次月考数学试题广东省信宜市第二中学2021-2022学年高二下学期月考一数学试题河南省濮阳市2021-2022学年高二下学期学业质量监测(升级)考试文科数学试题(已下线)2022年新高考北京数学高考真题变式题9-12题河南省濮阳市2021-2022学年高二下学期学业质量监测(升级)考试理科数学试题四川省内江市第六中学2021-2022学年高二下学期第一次月考数学(文科)试题四川省内江市第六中学2021-2022学年高二下学期第一次月考数学(理科)试题(已下线)2022年新高考北京数学高考真题变式题19-21题黑龙江省哈尔滨市哈尔滨德强高级中学2022-2023学年高二上学期10月月考数学试题湖北省黄冈市黄梅国际育才高级中学2022-2023学年高二上学期期中数学试题江苏省连云港市赣榆区赣马高级中学2022-2023学年高二上学期10月第一次检测数学试题(已下线)3.1.2椭圆的简单几何性质(第1课时)(分层作业)(3种题型分类基础练+能力提升练)-【上好课】高二数学同步备课系列(人教A版2019选择性必修第一册)湖北省黄冈市黄梅国际育才高级中学2023-2024学年高二上学期期中数学试题(已下线) 第3章 圆锥曲线的方程单元测试能力卷-2023-2024学年高二数学上学期人教A版(2019)选择性必修第一册
名校
解题方法
2 . 已知椭圆 过点
过点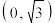 ,且离心率为
,且离心率为 .设
.设 ,
, 为椭圆
为椭圆 的左、右顶点,
的左、右顶点, 为椭圆上异于
为椭圆上异于 ,
, 的一点,直线
的一点,直线 ,
, 分别与直线
分别与直线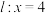 相交于
相交于 ,
, 两点,且直线
两点,且直线 与椭圆
与椭圆 交于另一点
交于另一点 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)求证:直线 与
与 的斜率之积为定值;
的斜率之积为定值;
(3)判断三点 ,
, ,
, 是否共线:并证明你的结论.
是否共线:并证明你的结论.
 过点
过点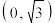 ,且离心率为
,且离心率为 .设
.设 ,
, 为椭圆
为椭圆 的左、右顶点,
的左、右顶点, 为椭圆上异于
为椭圆上异于 ,
, 的一点,直线
的一点,直线 ,
, 分别与直线
分别与直线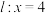 相交于
相交于 ,
, 两点,且直线
两点,且直线 与椭圆
与椭圆 交于另一点
交于另一点 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)求证:直线
 与
与 的斜率之积为定值;
的斜率之积为定值;(3)判断三点
 ,
, ,
, 是否共线:并证明你的结论.
是否共线:并证明你的结论.
您最近一年使用:0次
2022-10-11更新
|
1675次组卷
|
9卷引用:天津市滨海新区塘沽紫云中学2024届高三上学期期末模拟数学试题(六)
名校
解题方法
3 . 如图,在三棱柱 中,
中, 平面
平面 ,
,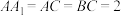 ,
, ,
, 分别是
分别是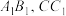 的中点
的中点
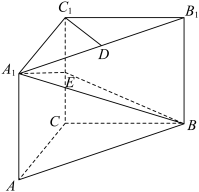
(1)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(2)在棱 上是否存在一点
上是否存在一点 ,使得平面
,使得平面 与平面
与平面 的夹角的余弦值为
的夹角的余弦值为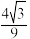 ?若存在,求出
?若存在,求出 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
 中,
中, 平面
平面 ,
,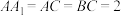 ,
, ,
, 分别是
分别是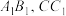 的中点
的中点
(1)求直线
 与平面
与平面 所成角的正弦值;
所成角的正弦值;(2)在棱
 上是否存在一点
上是否存在一点 ,使得平面
,使得平面 与平面
与平面 的夹角的余弦值为
的夹角的余弦值为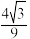 ?若存在,求出
?若存在,求出 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
您最近一年使用:0次
2021-11-12更新
|
975次组卷
|
3卷引用:天津市静海一中、杨村一中等五校2021-2022学年高二上学期期中联考数学试题
名校
4 . 如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
,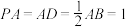 ,点E、M分别在线段
,点E、M分别在线段 、
、 上,且
上,且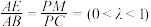 ,连接
,连接 ,延长
,延长 与
与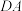 的延长线交于点F,连接
的延长线交于点F,连接 ,
, .
.

(1)求证: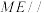 平面
平面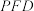 ;
;
(2)若 时,求平面
时,求平面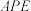 与平面
与平面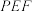 所成角的正弦值;
所成角的正弦值;
(3)若直线 与平面
与平面 所成角的正切值为
所成角的正切值为 ,求
,求 值.
值.
 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
,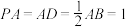 ,点E、M分别在线段
,点E、M分别在线段 、
、 上,且
上,且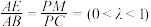 ,连接
,连接 ,延长
,延长 与
与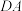 的延长线交于点F,连接
的延长线交于点F,连接 ,
, .
.
(1)求证:
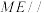 平面
平面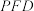 ;
;(2)若
 时,求平面
时,求平面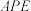 与平面
与平面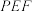 所成角的正弦值;
所成角的正弦值;(3)若直线
 与平面
与平面 所成角的正切值为
所成角的正切值为 ,求
,求 值.
值.
您最近一年使用:0次
5 . 四棱锥 中,底面
中,底面 为矩形
为矩形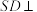 底面
底面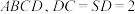 ,点M是侧棱
,点M是侧棱 的中点,
的中点,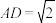 .
.
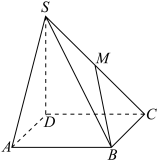
(1)求异面直线 与
与 所成角的大小;
所成角的大小;
(2)求二面角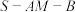 的正弦值.
的正弦值.
 中,底面
中,底面 为矩形
为矩形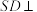 底面
底面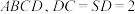 ,点M是侧棱
,点M是侧棱 的中点,
的中点,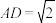 .
.
(1)求异面直线
 与
与 所成角的大小;
所成角的大小;(2)求二面角
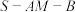 的正弦值.
的正弦值.
您最近一年使用:0次
名校
6 . 如图,在四棱锥 中,平面
中,平面 平面
平面 ,
, ,
, ,
, ,
, ,
,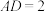 ,
,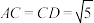 .
.
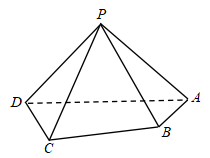
(1)求证: 平面
平面 ;
;
(2)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3)在棱 上是否存在点
上是否存在点 ,使得平面
,使得平面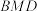 与平面
与平面 所成的锐二面角余弦值为
所成的锐二面角余弦值为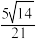 ?若存在,求
?若存在,求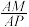 的值;若不存在、说明理由.
的值;若不存在、说明理由.
 中,平面
中,平面 平面
平面 ,
, ,
, ,
, ,
, ,
,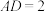 ,
,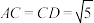 .
.
(1)求证:
 平面
平面 ;
;(2)求直线
 与平面
与平面 所成角的正弦值;
所成角的正弦值;(3)在棱
 上是否存在点
上是否存在点 ,使得平面
,使得平面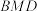 与平面
与平面 所成的锐二面角余弦值为
所成的锐二面角余弦值为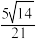 ?若存在,求
?若存在,求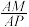 的值;若不存在、说明理由.
的值;若不存在、说明理由.
您最近一年使用:0次
7 . 已知椭圆 :
: (
( )的长轴长为4,离心率为
)的长轴长为4,离心率为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设椭圆 的左焦点为
的左焦点为 ,右顶点为
,右顶点为 ,过点
,过点 的直线与
的直线与 轴正半轴交于点
轴正半轴交于点 ,与椭圆交于点
,与椭圆交于点 ,且
,且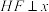 轴,过点
轴,过点 的另一直线与椭圆交于
的另一直线与椭圆交于 ,
, 两点,若
两点,若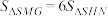 ,求直线
,求直线 的方程.
的方程.
 :
: (
( )的长轴长为4,离心率为
)的长轴长为4,离心率为 .
.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)设椭圆
 的左焦点为
的左焦点为 ,右顶点为
,右顶点为 ,过点
,过点 的直线与
的直线与 轴正半轴交于点
轴正半轴交于点 ,与椭圆交于点
,与椭圆交于点 ,且
,且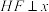 轴,过点
轴,过点 的另一直线与椭圆交于
的另一直线与椭圆交于 ,
, 两点,若
两点,若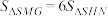 ,求直线
,求直线 的方程.
的方程.
您最近一年使用:0次
2021-05-06更新
|
1976次组卷
|
6卷引用:天津市河北区2021届高三一模数学试题
天津市河北区2021届高三一模数学试题天津市耀华中学2021-2022学年高三上学期第一次月考数学试题天津市静海区第一中学2021-2022学年高三上学期第四次阶段检测数学试题天津市九校2024届高三下学期联合模拟考试(一)数学试卷广西玉林市育才中学2021届高三5月三模数学(文)试题(已下线)专题42 盘点圆锥曲线中的面积问题——备战2022年高考数学二轮复习常考点专题突破
名校
解题方法
8 . 如图,在三棱柱 中,
中, 平面
平面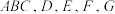 分别为
分别为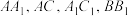 的中点,
的中点,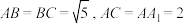
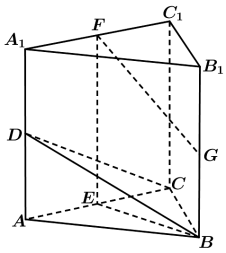
(1)求证: 平面
平面 ;
;
(2)求二面角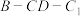 的正弦值;
的正弦值;
(3)求直线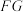 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,
中, 平面
平面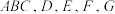 分别为
分别为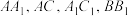 的中点,
的中点,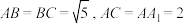

(1)求证:
 平面
平面 ;
;(2)求二面角
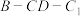 的正弦值;
的正弦值;(3)求直线
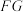 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2021-05-03更新
|
1591次组卷
|
3卷引用:天津市河西区2021届高三下学期总复习质量调查(二)数学试题
名校
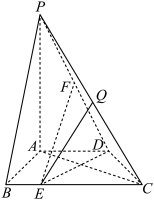
9 . 如图,在四棱锥 中,
中, 平面
平面 ,底面
,底面 是直角梯形,其中
是直角梯形,其中 ,
, ,
,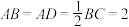 ,
, ,E为棱
,E为棱 上的点,且
上的点,且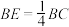 .
.
(1)若F为棱 的中点,求证:
的中点,求证: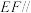 平面
平面 ;
;
(2)(i)求证 平面
平面 ;
;
(ii)设Q为棱 上的点(不与C,P重合),且直线
上的点(不与C,P重合),且直线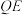 与平面
与平面 所成角的正弦值为
所成角的正弦值为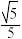 ,求
,求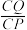 的值.
的值.
 中,
中, 平面
平面 ,底面
,底面 是直角梯形,其中
是直角梯形,其中 ,
, ,
,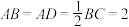 ,
, ,E为棱
,E为棱 上的点,且
上的点,且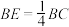 .
.
(1)若F为棱
 的中点,求证:
的中点,求证: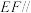 平面
平面 ;
;(2)(i)求证
 平面
平面 ;
;(ii)设Q为棱
 上的点(不与C,P重合),且直线
上的点(不与C,P重合),且直线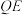 与平面
与平面 所成角的正弦值为
所成角的正弦值为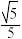 ,求
,求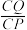 的值.
的值.
您最近一年使用:0次
2021-04-11更新
|
1098次组卷
|
4卷引用:天津市耀华中学2022届高三暑假线上调研数学试题
天津市耀华中学2022届高三暑假线上调研数学试题北京市清华大学附属中学2020-2021学年高二上学期期末考试数学试题(已下线)专题02 空间向量与立体几何的典型题(二)-【尖子生专用】2021-2022学年高二数学考点培优训练(人教A版2019选择性必修第一册)(已下线)一轮复习大题专练50—立体几何(线面角2)—2022届高三数学一轮复习
解题方法
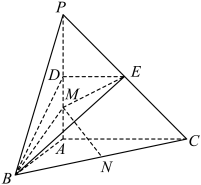
10 . 如图,在三棱锥 中,
中, 底面
底面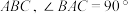 .点D,E,N分别为棱
.点D,E,N分别为棱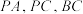 的中点,M是线段
的中点,M是线段 的中点,
的中点,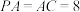 ,
, .
.
(Ⅰ)求证: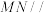 平面
平面 ;
;
(Ⅱ)求二面角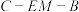 的正弦值;
的正弦值;
(Ⅲ)已知点H在棱 上,且直线
上,且直线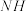 与直线
与直线 所成角的余弦值为
所成角的余弦值为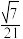 ,求线段
,求线段 的长.
的长.
 中,
中, 底面
底面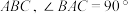 .点D,E,N分别为棱
.点D,E,N分别为棱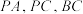 的中点,M是线段
的中点,M是线段 的中点,
的中点,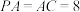 ,
, .
.
(Ⅰ)求证:
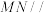 平面
平面 ;
;(Ⅱ)求二面角
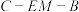 的正弦值;
的正弦值;(Ⅲ)已知点H在棱
 上,且直线
上,且直线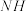 与直线
与直线 所成角的余弦值为
所成角的余弦值为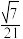 ,求线段
,求线段 的长.
的长.
您最近一年使用:0次



