名校
解题方法
1 . 若一个椭圆的焦距为质数,且离心率的倒数也为质数,则称这样的椭圆为“质朴椭圆”.
(1)证明:椭圆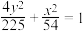 为“质朴椭圆”.
为“质朴椭圆”.
(2)是否存在实数 ,使得椭圆
,使得椭圆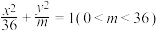 为“质朴椭圆”?若存在,求
为“质朴椭圆”?若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(3)设斜率为 的直线
的直线 经过椭圆
经过椭圆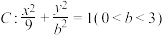 的右焦点,且与
的右焦点,且与 交于
交于 ,
, 两点,
两点,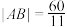 ,试问
,试问 是否为“质朴椭圆”,说明你的理由.
是否为“质朴椭圆”,说明你的理由.
(1)证明:椭圆
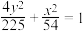 为“质朴椭圆”.
为“质朴椭圆”.(2)是否存在实数
 ,使得椭圆
,使得椭圆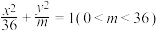 为“质朴椭圆”?若存在,求
为“质朴椭圆”?若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.(3)设斜率为
 的直线
的直线 经过椭圆
经过椭圆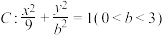 的右焦点,且与
的右焦点,且与 交于
交于 ,
, 两点,
两点,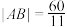 ,试问
,试问 是否为“质朴椭圆”,说明你的理由.
是否为“质朴椭圆”,说明你的理由.
您最近一年使用:0次
2 . 已知双曲线 的左、右焦点分别为
的左、右焦点分别为 ,
, ,且焦距为4,左顶点为E,过右焦点
,且焦距为4,左顶点为E,过右焦点 的动直线l交C于A,B两点,当l垂直于x轴时,
的动直线l交C于A,B两点,当l垂直于x轴时, .
.
(1)求C的方程;
(2)若动直线l与C的左支交于点A,右支交于点B,求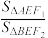 的取值范围.
的取值范围.
 的左、右焦点分别为
的左、右焦点分别为 ,
, ,且焦距为4,左顶点为E,过右焦点
,且焦距为4,左顶点为E,过右焦点 的动直线l交C于A,B两点,当l垂直于x轴时,
的动直线l交C于A,B两点,当l垂直于x轴时, .
.(1)求C的方程;
(2)若动直线l与C的左支交于点A,右支交于点B,求
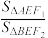 的取值范围.
的取值范围.
您最近一年使用:0次
3 . 已知点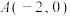 ,
, ,动点
,动点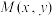 满足直线
满足直线 与
与 的斜率之积为
的斜率之积为 .记
.记 的轨迹为曲线
的轨迹为曲线 .
.
(1)求 的方程,并说明
的方程,并说明 是什么曲线;
是什么曲线;
(2)过坐标原点的直线 交
交 于
于 ,
, 两点,点
两点,点 在第一象限,
在第一象限, 轴,垂足为
轴,垂足为 ,连结
,连结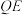 并延长交
并延长交 于点
于点 .
.
(ⅰ)证明:以 为直径的圆必然经过点
为直径的圆必然经过点 .
.
(ⅱ)求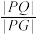 的取值范围,并求当
的取值范围,并求当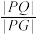 取得最小值时的直线
取得最小值时的直线 的方程.
的方程.
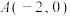 ,
, ,动点
,动点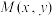 满足直线
满足直线 与
与 的斜率之积为
的斜率之积为 .记
.记 的轨迹为曲线
的轨迹为曲线 .
.(1)求
 的方程,并说明
的方程,并说明 是什么曲线;
是什么曲线;(2)过坐标原点的直线
 交
交 于
于 ,
, 两点,点
两点,点 在第一象限,
在第一象限, 轴,垂足为
轴,垂足为 ,连结
,连结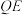 并延长交
并延长交 于点
于点 .
.(ⅰ)证明:以
 为直径的圆必然经过点
为直径的圆必然经过点 .
.(ⅱ)求
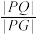 的取值范围,并求当
的取值范围,并求当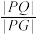 取得最小值时的直线
取得最小值时的直线 的方程.
的方程.
您最近一年使用:0次
名校
解题方法
4 . 已知动圆 经过点
经过点 且与直线
且与直线 相切,记圆心
相切,记圆心 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线 的方程;
的方程;
(2)设过点 且斜率为正的直线
且斜率为正的直线 交曲线
交曲线 于
于 两点(点
两点(点 在点
在点 的上方),
的上方), 的中点为
的中点为 ,
,
①过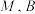 作直线
作直线 的垂线,垂足分别为
的垂线,垂足分别为 ,试证明:
,试证明: ;
;
②设线段 的垂直平分线交
的垂直平分线交 轴于点
轴于点 ,若
,若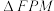 的面积为4,求直线
的面积为4,求直线 的方程.
的方程.
 经过点
经过点 且与直线
且与直线 相切,记圆心
相切,记圆心 的轨迹为曲线
的轨迹为曲线 .
.(1)求曲线
 的方程;
的方程;(2)设过点
 且斜率为正的直线
且斜率为正的直线 交曲线
交曲线 于
于 两点(点
两点(点 在点
在点 的上方),
的上方), 的中点为
的中点为 ,
,①过
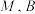 作直线
作直线 的垂线,垂足分别为
的垂线,垂足分别为 ,试证明:
,试证明: ;
;②设线段
 的垂直平分线交
的垂直平分线交 轴于点
轴于点 ,若
,若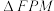 的面积为4,求直线
的面积为4,求直线 的方程.
的方程.
您最近一年使用:0次
2024-10-17更新
|
838次组卷
|
2卷引用:四川省巴中市2025届高三上学期“零诊”考试数学试题
名校
解题方法
5 . 已知 是椭圆
是椭圆 的右焦点,过点
的右焦点,过点 作两条相互垂直的动直线
作两条相互垂直的动直线 和
和 ,
, 与
与 交于
交于 ,
, 两点,
两点, 与
与 交于
交于 ,
, 两点.
两点.
(1)若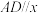 轴,求
轴,求 ;
;
(2)设 ,
, 分别为线段
分别为线段 ,
, 的中点,求证:直线
的中点,求证:直线 过定点
过定点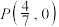 .
.
 是椭圆
是椭圆 的右焦点,过点
的右焦点,过点 作两条相互垂直的动直线
作两条相互垂直的动直线 和
和 ,
, 与
与 交于
交于 ,
, 两点,
两点, 与
与 交于
交于 ,
, 两点.
两点.(1)若
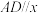 轴,求
轴,求 ;
;(2)设
 ,
, 分别为线段
分别为线段 ,
, 的中点,求证:直线
的中点,求证:直线 过定点
过定点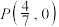 .
.
您最近一年使用:0次
2024-09-28更新
|
352次组卷
|
2卷引用:湖南省常德市西洞庭管理区第一中学等多校2025届高三上学期9月联考数学试题
名校
解题方法
6 . 抛物线 的焦点为
的焦点为 ,准线为
,准线为 ,斜率分别为
,斜率分别为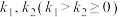 的直线
的直线 均过点
均过点 ,且分别与
,且分别与 交于
交于 和
和 (其中
(其中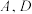 在第一象限),
在第一象限),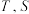 分别为
分别为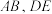 的中点,直线
的中点,直线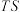 与
与 交于点
交于点 ,
,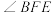 的角平分线与
的角平分线与 交于点
交于点 .
.
(1)求直线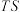 的斜率(用
的斜率(用 表示);
表示);
(2)证明: 的面积大于
的面积大于 .
.
 的焦点为
的焦点为 ,准线为
,准线为 ,斜率分别为
,斜率分别为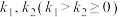 的直线
的直线 均过点
均过点 ,且分别与
,且分别与 交于
交于 和
和 (其中
(其中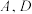 在第一象限),
在第一象限),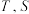 分别为
分别为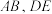 的中点,直线
的中点,直线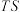 与
与 交于点
交于点 ,
,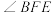 的角平分线与
的角平分线与 交于点
交于点 .
.(1)求直线
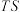 的斜率(用
的斜率(用 表示);
表示);(2)证明:
 的面积大于
的面积大于 .
.
您最近一年使用:0次
2024-09-23更新
|
385次组卷
|
3卷引用:山东省烟台市招远市第二中学等校2025届高三上学期摸底联考数学试题
2025高三·全国·专题练习
解题方法
7 . 已知椭圆 的左、右焦点分别为
的左、右焦点分别为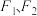 ,且
,且 在抛物线
在抛物线 的准线上,点
的准线上,点 是
是 上的一个动点,
上的一个动点, 面积的最大值为
面积的最大值为 .
.
(1)求 的方程;
的方程;
(2)设经过 右焦点
右焦点 且斜率不为0的直线交
且斜率不为0的直线交 于
于 两点,线段
两点,线段 的垂直平分线交
的垂直平分线交 轴于点
轴于点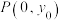 ,求
,求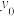 的取值范围.
的取值范围.
 的左、右焦点分别为
的左、右焦点分别为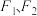 ,且
,且 在抛物线
在抛物线 的准线上,点
的准线上,点 是
是 上的一个动点,
上的一个动点, 面积的最大值为
面积的最大值为 .
.(1)求
 的方程;
的方程;(2)设经过
 右焦点
右焦点 且斜率不为0的直线交
且斜率不为0的直线交 于
于 两点,线段
两点,线段 的垂直平分线交
的垂直平分线交 轴于点
轴于点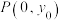 ,求
,求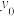 的取值范围.
的取值范围.
您最近一年使用:0次
解题方法
8 . 已知P为双曲线C: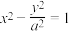 上一点,O为坐标原点,线段OP的垂直平分线与双曲线C相切.
上一点,O为坐标原点,线段OP的垂直平分线与双曲线C相切.
(1)若点P是直线 与圆
与圆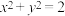 的交点,求a;
的交点,求a;
(2)求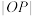 的取值范围.
的取值范围.
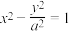 上一点,O为坐标原点,线段OP的垂直平分线与双曲线C相切.
上一点,O为坐标原点,线段OP的垂直平分线与双曲线C相切.(1)若点P是直线
 与圆
与圆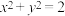 的交点,求a;
的交点,求a;(2)求
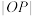 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
9 . 已知  为抛物线
为抛物线 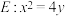 的焦点, 过点
的焦点, 过点 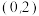 的直线
的直线  与抛物线
与抛物线  交于
交于  两点, 抛物线
两点, 抛物线  在
在  两点处的切线交于点
两点处的切线交于点  .
.
(1)设 是抛物线
是抛物线  上一点, 证明: 抛物线
上一点, 证明: 抛物线  在点
在点  处的切线方程为
处的切线方程为 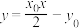 , 并利用切线方程求点
, 并利用切线方程求点  的纵坐标的值;
的纵坐标的值;
(2)点 为抛物线
为抛物线  上异于
上异于  的点, 过点
的点, 过点  作抛物线
作抛物线  的切线, 分别与线段
的切线, 分别与线段 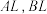 交于
交于  .
.
(i)若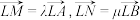 ,求
,求  的值;
的值;
(ii)证明: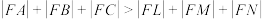
 为抛物线
为抛物线 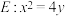 的焦点, 过点
的焦点, 过点 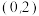 的直线
的直线  与抛物线
与抛物线  交于
交于  两点, 抛物线
两点, 抛物线  在
在  两点处的切线交于点
两点处的切线交于点  .
.(1)设
 是抛物线
是抛物线  上一点, 证明: 抛物线
上一点, 证明: 抛物线  在点
在点  处的切线方程为
处的切线方程为 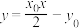 , 并利用切线方程求点
, 并利用切线方程求点  的纵坐标的值;
的纵坐标的值;(2)点
 为抛物线
为抛物线  上异于
上异于  的点, 过点
的点, 过点  作抛物线
作抛物线  的切线, 分别与线段
的切线, 分别与线段 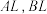 交于
交于  .
.(i)若
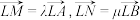 ,求
,求  的值;
的值;(ii)证明:
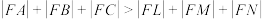
您最近一年使用:0次
名校
解题方法
10 . 在平面直角坐标系 中,抛物线
中,抛物线 的焦点到准线的距离等于椭圆
的焦点到准线的距离等于椭圆 的短轴长,点
的短轴长,点 在抛物线
在抛物线 上,圆
上,圆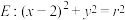 (其中
(其中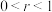 ).
).
(1)若 为圆
为圆 上的动点,求线段
上的动点,求线段 长度的最小值;
长度的最小值;
(2)设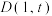 是抛物线
是抛物线 上位于第一象限的一点,过
上位于第一象限的一点,过 作圆
作圆 的两条切线,分别交抛物线
的两条切线,分别交抛物线 于点
于点 .证明:直线
.证明:直线 经过定点.
经过定点.
 中,抛物线
中,抛物线 的焦点到准线的距离等于椭圆
的焦点到准线的距离等于椭圆 的短轴长,点
的短轴长,点 在抛物线
在抛物线 上,圆
上,圆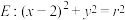 (其中
(其中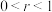 ).
).(1)若
 为圆
为圆 上的动点,求线段
上的动点,求线段 长度的最小值;
长度的最小值;(2)设
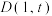 是抛物线
是抛物线 上位于第一象限的一点,过
上位于第一象限的一点,过 作圆
作圆 的两条切线,分别交抛物线
的两条切线,分别交抛物线 于点
于点 .证明:直线
.证明:直线 经过定点.
经过定点.
您最近一年使用:0次



