1 . 空间向量的叉乘是三维欧几里得空间中定义的一种新运算,它可以用来描述空间向量之间的垂直关系.设空间向量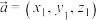 ,
, ,则
,则 叉乘
叉乘 的运算公式为
的运算公式为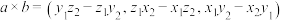
(1)证明: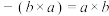 .
.
(2)设 ,
, ,
, 是平面
是平面 内不共线的三个不同的点.
内不共线的三个不同的点.
①证明: 是平面
是平面 的一个法向量.
的一个法向量.
②说明 的几何意义(即说明
的几何意义(即说明 的长度与方向的几何意义).
的长度与方向的几何意义).
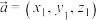 ,
, ,则
,则 叉乘
叉乘 的运算公式为
的运算公式为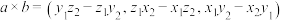
(1)证明:
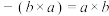 .
.(2)设
 ,
, ,
, 是平面
是平面 内不共线的三个不同的点.
内不共线的三个不同的点.①证明:
 是平面
是平面 的一个法向量.
的一个法向量.②说明
 的几何意义(即说明
的几何意义(即说明 的长度与方向的几何意义).
的长度与方向的几何意义).
您最近一年使用:0次
名校
解题方法
2 . 球面三角学是研究球面三角形的边、角关系的一门学科.如图一,球 的半径为
的半径为 ,
, 为球面上三点,劣弧
为球面上三点,劣弧 的弧长记为
的弧长记为 ,设
,设 表示以
表示以 为圆心,且过
为圆心,且过 的圆,同理,圆
的圆,同理,圆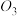 ,
, 的劣弧
的劣弧 的弧长分别记为
的弧长分别记为 ,曲面
,曲面 (阴影部分)叫做球面三角形,若设二面角
(阴影部分)叫做球面三角形,若设二面角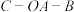 ,
,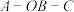 ,
, 分别为
分别为 ,
, ,
, ,则球面三角形的面积为
,则球面三角形的面积为 .
. ,平面
,平面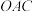 ,平面
,平面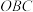 两两垂直,求球面三角形
两两垂直,求球面三角形 的面积;
的面积;
(2)若将图一中四面体 截出得到图二,若平面三角形
截出得到图二,若平面三角形 为直角三角形,
为直角三角形,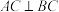 ,设
,设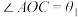 ,
, ,
,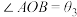 .
.
①求证: ;
;
②延长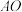 与球
与球 交于点
交于点 ,连接
,连接 ,若直线
,若直线 与平面
与平面 所成的角分别为
所成的角分别为 ,
, ,
, ,
,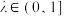 ,
, 为
为 中点,
中点, 为
为 中点,设平面
中点,设平面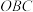 与平面
与平面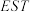 的夹角为
的夹角为 ,求
,求 的最小值.
的最小值.
 的半径为
的半径为 ,
, 为球面上三点,劣弧
为球面上三点,劣弧 的弧长记为
的弧长记为 ,设
,设 表示以
表示以 为圆心,且过
为圆心,且过 的圆,同理,圆
的圆,同理,圆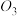 ,
, 的劣弧
的劣弧 的弧长分别记为
的弧长分别记为 ,曲面
,曲面 (阴影部分)叫做球面三角形,若设二面角
(阴影部分)叫做球面三角形,若设二面角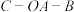 ,
,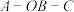 ,
, 分别为
分别为 ,
, ,
, ,则球面三角形的面积为
,则球面三角形的面积为 .
.
 ,平面
,平面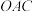 ,平面
,平面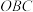 两两垂直,求球面三角形
两两垂直,求球面三角形 的面积;
的面积;(2)若将图一中四面体
 截出得到图二,若平面三角形
截出得到图二,若平面三角形 为直角三角形,
为直角三角形,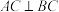 ,设
,设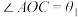 ,
, ,
,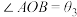 .
.①求证:
 ;
;②延长
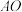 与球
与球 交于点
交于点 ,连接
,连接 ,若直线
,若直线 与平面
与平面 所成的角分别为
所成的角分别为 ,
, ,
, ,
,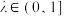 ,
, 为
为 中点,
中点, 为
为 中点,设平面
中点,设平面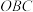 与平面
与平面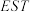 的夹角为
的夹角为 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
2024-10-16更新
|
253次组卷
|
4卷引用:河北省沧州市2024-2025学年高二上学期9月月考数学试题
解题方法
3 . 定义:由椭圆的一个焦点和长轴的一个顶点(焦点与顶点在同一边)和短轴的一个顶点组成的三角形称为该椭圆的“焦顶三角形”,如果两个椭圆的”焦顶三角形”相似,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比,下列问题中( 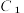 对应图1,
对应图1, 对应图2).
对应图2).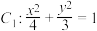 与椭圆
与椭圆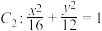 是否是“相似椭圆”? 若是,求出相似比;若不是,请说明理由;
是否是“相似椭圆”? 若是,求出相似比;若不是,请说明理由;
(2)证明:两个椭圆是“相似椭圆”的充要条件是离心率相等;
(3)已知椭圆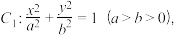 椭圆
椭圆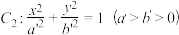 的离心率为
的离心率为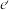 ,
,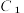 与
与
是 “相似椭圆 ”,且 与
与 的相似比为
的相似比为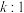 ,若
,若 的面积为
的面积为 ,求
,求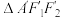 的面积(用
的面积(用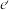 ,
, ,
, 表示).
表示).
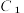 对应图1,
对应图1, 对应图2).
对应图2).
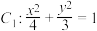 与椭圆
与椭圆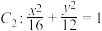 是否是“相似椭圆”? 若是,求出相似比;若不是,请说明理由;
是否是“相似椭圆”? 若是,求出相似比;若不是,请说明理由;(2)证明:两个椭圆是“相似椭圆”的充要条件是离心率相等;
(3)已知椭圆
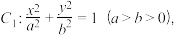 椭圆
椭圆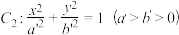 的离心率为
的离心率为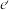 ,
,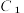 与
与
 与
与 的相似比为
的相似比为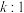 ,若
,若 的面积为
的面积为 ,求
,求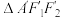 的面积(用
的面积(用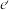 ,
, ,
, 表示).
表示).
您最近一年使用:0次
2024-10-13更新
|
256次组卷
|
2卷引用:江西省赣州市2024-2025学年高二上学期10月检测数学试卷
解题方法
4 . 阿波罗尼斯是古希腊著名数学家,他的主要研究成果集中在他的代表作《圆锥曲线论》一书中,阿波罗尼斯圆是他的研究成果之一,指的是平面内动点 与两定点
与两定点 的距离的比值
的距离的比值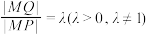 是个常数,那么动点
是个常数,那么动点 的轨迹就是阿波罗尼斯圆,圆心在直线
的轨迹就是阿波罗尼斯圆,圆心在直线 上.已知动点
上.已知动点 的轨迹是阿波罗尼斯圆,其方程为
的轨迹是阿波罗尼斯圆,其方程为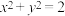 ,定点分别为椭圆
,定点分别为椭圆 的右焦点
的右焦点 与右顶点
与右顶点 ,且椭圆
,且椭圆 的离心率为
的离心率为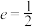 .
. 的标准方程;
的标准方程;
(2)如图,过点 斜率为
斜率为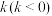 的直线
的直线 与椭圆
与椭圆 相交于
相交于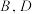 (点
(点 在
在 轴上方)两点,点
轴上方)两点,点 是椭圆
是椭圆 上异于
上异于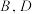 的两点,
的两点,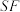 平分
平分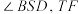 平分
平分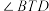 .
.
①求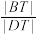 的取值范围;
的取值范围;
②将点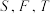 看作一个阿波罗尼斯圆上的三点,若
看作一个阿波罗尼斯圆上的三点,若 外接圆的周长为
外接圆的周长为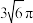 ,求直线
,求直线 的方程.
的方程.
 与两定点
与两定点 的距离的比值
的距离的比值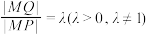 是个常数,那么动点
是个常数,那么动点 的轨迹就是阿波罗尼斯圆,圆心在直线
的轨迹就是阿波罗尼斯圆,圆心在直线 上.已知动点
上.已知动点 的轨迹是阿波罗尼斯圆,其方程为
的轨迹是阿波罗尼斯圆,其方程为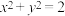 ,定点分别为椭圆
,定点分别为椭圆 的右焦点
的右焦点 与右顶点
与右顶点 ,且椭圆
,且椭圆 的离心率为
的离心率为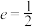 .
.
 的标准方程;
的标准方程;(2)如图,过点
 斜率为
斜率为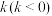 的直线
的直线 与椭圆
与椭圆 相交于
相交于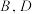 (点
(点 在
在 轴上方)两点,点
轴上方)两点,点 是椭圆
是椭圆 上异于
上异于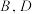 的两点,
的两点,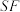 平分
平分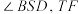 平分
平分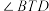 .
.①求
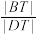 的取值范围;
的取值范围;②将点
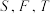 看作一个阿波罗尼斯圆上的三点,若
看作一个阿波罗尼斯圆上的三点,若 外接圆的周长为
外接圆的周长为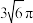 ,求直线
,求直线 的方程.
的方程.
您最近一年使用:0次
2024-05-16更新
|
794次组卷
|
3卷引用:安徽省皖南八校2024届高三4月第三次联考数学试卷
名校
解题方法
5 . 三等分角是古希腊几何尺规作图的三大问题之一,如今数学上已经证明三等分任意角是尺规作图不可能问题,如果不局限于尺规,三等分任意角是可能的.下面是数学家帕普斯给出的一种三等分角的方法:已知角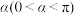 的顶点为
的顶点为 ,在
,在 的两边上截取
的两边上截取 ,连接
,连接 ,在线段
,在线段 上取一点
上取一点 ,使得
,使得 ,记
,记 的中点为
的中点为 ,以
,以 为中心,
为中心, 为顶点作离心率为2的双曲线
为顶点作离心率为2的双曲线 ,以
,以 为圆心,
为圆心, 为半径作圆,与双曲线
为半径作圆,与双曲线 左支交于点
左支交于点 (射线
(射线 在
在 内部),则
内部),则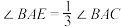 .在上述作法中,以
.在上述作法中,以 为原点,直线
为原点,直线 为
为 轴建立如图所示的平面直角坐标系,若
轴建立如图所示的平面直角坐标系,若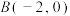 ,点
,点 在
在 轴的上方.
轴的上方. 的方程;
的方程;
(2)若过点 且与
且与 轴垂直的直线交
轴垂直的直线交 轴于点
轴于点 ,点
,点 到直线
到直线 的距离为
的距离为 .
.
证明:①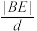 为定值;
为定值;
②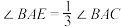 .
.
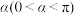 的顶点为
的顶点为 ,在
,在 的两边上截取
的两边上截取 ,连接
,连接 ,在线段
,在线段 上取一点
上取一点 ,使得
,使得 ,记
,记 的中点为
的中点为 ,以
,以 为中心,
为中心, 为顶点作离心率为2的双曲线
为顶点作离心率为2的双曲线 ,以
,以 为圆心,
为圆心, 为半径作圆,与双曲线
为半径作圆,与双曲线 左支交于点
左支交于点 (射线
(射线 在
在 内部),则
内部),则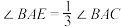 .在上述作法中,以
.在上述作法中,以 为原点,直线
为原点,直线 为
为 轴建立如图所示的平面直角坐标系,若
轴建立如图所示的平面直角坐标系,若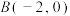 ,点
,点 在
在 轴的上方.
轴的上方.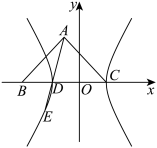
 的方程;
的方程;(2)若过点
 且与
且与 轴垂直的直线交
轴垂直的直线交 轴于点
轴于点 ,点
,点 到直线
到直线 的距离为
的距离为 .
.证明:①
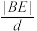 为定值;
为定值;②
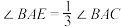 .
.
您最近一年使用:0次
名校
解题方法
6 . 已知平面内的动点M的轨迹是阿波罗尼斯圆(动点M与两定点A,B的距离之比 (
( ,
,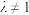 ,且
,且 是一个常数),其方程为
是一个常数),其方程为 ,定点分别为椭圆
,定点分别为椭圆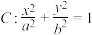
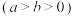 的右焦点F与右顶点A,且椭圆C的长轴长为
的右焦点F与右顶点A,且椭圆C的长轴长为 .
.
(1)求椭圆C的标准方程;
(2)设椭圆C的左焦点为E,过点A作直线l交圆 于点S,T,求
于点S,T,求 面积的最大值.
面积的最大值.
 (
( ,
,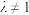 ,且
,且 是一个常数),其方程为
是一个常数),其方程为 ,定点分别为椭圆
,定点分别为椭圆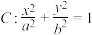
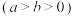 的右焦点F与右顶点A,且椭圆C的长轴长为
的右焦点F与右顶点A,且椭圆C的长轴长为 .
.(1)求椭圆C的标准方程;
(2)设椭圆C的左焦点为E,过点A作直线l交圆
 于点S,T,求
于点S,T,求 面积的最大值.
面积的最大值.
您最近一年使用:0次
2023-12-02更新
|
244次组卷
|
2卷引用:广东省东莞市东华高级中学2023-2024学年高二上学期期中考试数学试卷
名校
解题方法
7 . “工艺折纸”是一种把纸张折成各种不同形状物品的艺术活动,在我国源远流长.某些折纸活动蕴含丰富的数学内容,例如:用一张圆形纸片,按如下步骤折纸(如图)
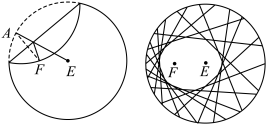
步骤1:设圆心是E,在圆内异于圆心处取一点,标记为F;
步骤2:把纸片折叠,使圆周正好通过点F;
步骤3:把纸片展开,并留下一道折痕;
步骤4:不停重复步骤2和3,就能得到越来越多的折痕.
已知这些折痕所围成的图形是一个椭圆.若取半径为4的圆形纸片,设定点F到圆心E的距离为 ,按上述方法折纸.
,按上述方法折纸.
(1)以点F、E所在的直线为x轴,建立适当的坐标系,求折痕围成的椭圆C的标准方程;
(2)设椭圆C的下顶点为D,过点D作两条互相垂直的直线 ,
, ,这两条直线与椭圆C的另一个交点分别为M,N.设
,这两条直线与椭圆C的另一个交点分别为M,N.设 的斜率为
的斜率为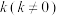 ,△DMN的面积为S,当
,△DMN的面积为S,当 时,求k的取值范围.
时,求k的取值范围.

步骤1:设圆心是E,在圆内异于圆心处取一点,标记为F;
步骤2:把纸片折叠,使圆周正好通过点F;
步骤3:把纸片展开,并留下一道折痕;
步骤4:不停重复步骤2和3,就能得到越来越多的折痕.
已知这些折痕所围成的图形是一个椭圆.若取半径为4的圆形纸片,设定点F到圆心E的距离为
 ,按上述方法折纸.
,按上述方法折纸.(1)以点F、E所在的直线为x轴,建立适当的坐标系,求折痕围成的椭圆C的标准方程;
(2)设椭圆C的下顶点为D,过点D作两条互相垂直的直线
 ,
, ,这两条直线与椭圆C的另一个交点分别为M,N.设
,这两条直线与椭圆C的另一个交点分别为M,N.设 的斜率为
的斜率为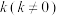 ,△DMN的面积为S,当
,△DMN的面积为S,当 时,求k的取值范围.
时,求k的取值范围.
您最近一年使用:0次
2023-05-01更新
|
901次组卷
|
4卷引用:江西省南昌市南昌县莲塘第一中学等2校2023届高三二模数学(文)试题
江西省南昌市南昌县莲塘第一中学等2校2023届高三二模数学(文)试题江西省南昌市2023届高三三模数学(文)试题(已下线)第五篇 向量与几何 专题8 帕斯卡定理、布列安桑定理、笛沙格定理、彭塞列闭合定理 微点3 笛沙格定理、彭塞列闭合定理江苏省江苏省南京人民中学、南通海安市实验中学2023-2024学年高二上学期10月月考数学试题
名校
解题方法
8 . “工艺折纸”是一种把纸张折成各种不同形状物品的艺术活动,在我国源远流长,某些折纸活动蕴含丰富的数学内容,例如:用一张纸片,按如下步骤折纸:
步骤1:在纸上画一个圆 ,并在圆外取一定点
,并在圆外取一定点 ;
;
步骤2:把纸片折叠,使得点 折叠后与圆
折叠后与圆 上某一点重合;
上某一点重合;
步骤3:把纸片展开,并得到一条折痕;
步骤4:不断重复步骤2和3,得到越来越多的折痕.
你会发现,当折痕足够密时,这些折痕会呈现出一个双曲线的轮廓.
若取一张足够大的纸,画一个半径为2的圆 ,并在圆外取一定点
,并在圆外取一定点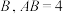 ,按照上述方法折纸,点
,按照上述方法折纸,点 折叠后与圆
折叠后与圆 上的点
上的点 重合,折痕与直线
重合,折痕与直线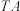 交于点
交于点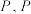 的轨迹为曲线
的轨迹为曲线 .
.
(1)以 所在直线为
所在直线为 轴建立适当的坐标系,求
轴建立适当的坐标系,求 的方程;
的方程;
(2)设 的中点为
的中点为 ,若存在一个定圆
,若存在一个定圆 ,使得当
,使得当 的弦
的弦 与圆
与圆 相切时,
相切时, 上存在异于
上存在异于 的点
的点 使得
使得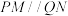 ,且直线
,且直线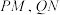 均与圆
均与圆 相切.
相切.
(i)求证: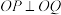 ;
;
(ii)求四边形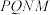 面积的取值范围.
面积的取值范围.
步骤1:在纸上画一个圆
 ,并在圆外取一定点
,并在圆外取一定点 ;
;步骤2:把纸片折叠,使得点
 折叠后与圆
折叠后与圆 上某一点重合;
上某一点重合;步骤3:把纸片展开,并得到一条折痕;
步骤4:不断重复步骤2和3,得到越来越多的折痕.
你会发现,当折痕足够密时,这些折痕会呈现出一个双曲线的轮廓.
若取一张足够大的纸,画一个半径为2的圆
 ,并在圆外取一定点
,并在圆外取一定点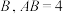 ,按照上述方法折纸,点
,按照上述方法折纸,点 折叠后与圆
折叠后与圆 上的点
上的点 重合,折痕与直线
重合,折痕与直线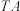 交于点
交于点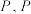 的轨迹为曲线
的轨迹为曲线 .
.(1)以
 所在直线为
所在直线为 轴建立适当的坐标系,求
轴建立适当的坐标系,求 的方程;
的方程;(2)设
 的中点为
的中点为 ,若存在一个定圆
,若存在一个定圆 ,使得当
,使得当 的弦
的弦 与圆
与圆 相切时,
相切时, 上存在异于
上存在异于 的点
的点 使得
使得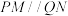 ,且直线
,且直线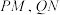 均与圆
均与圆 相切.
相切.(i)求证:
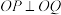 ;
;(ii)求四边形
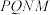 面积的取值范围.
面积的取值范围.
您最近一年使用:0次
名校
解题方法
9 . 法国数学家加斯帕尔·蒙日是19世纪著名的几何学家,他创立了画法几何学,推动了空间解析几何学的独立发展,奠定了空间微分几何学的宽厚基础,根据他的研究成果,我们定义:给定椭圆 :
: ,则称圆心在原点
,则称圆心在原点 ,半径是
,半径是 的圆为“椭圆
的圆为“椭圆 的伴随圆”,已知椭圆
的伴随圆”,已知椭圆 的一个焦点为
的一个焦点为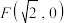 ,其短轴的一个端点到焦点
,其短轴的一个端点到焦点 的距离为
的距离为 .
. 为椭圆
为椭圆 的“伴随圆”与
的“伴随圆”与 轴正半轴的交点,
轴正半轴的交点, ,
, 是椭圆
是椭圆 的两相异点,且
的两相异点,且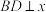 轴,求
轴,求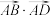 的取值范围.
的取值范围.
(2)在椭圆 的“伴随圆”上任取一点
的“伴随圆”上任取一点 ,过点
,过点 作直线
作直线 ,
, ,使得
,使得 ,
, 与椭圆
与椭圆 都只有一个交点,试判断
都只有一个交点,试判断 ,
, 是否垂直?并说明理由.
是否垂直?并说明理由.
 :
: ,则称圆心在原点
,则称圆心在原点 ,半径是
,半径是 的圆为“椭圆
的圆为“椭圆 的伴随圆”,已知椭圆
的伴随圆”,已知椭圆 的一个焦点为
的一个焦点为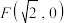 ,其短轴的一个端点到焦点
,其短轴的一个端点到焦点 的距离为
的距离为 .
.
 为椭圆
为椭圆 的“伴随圆”与
的“伴随圆”与 轴正半轴的交点,
轴正半轴的交点, ,
, 是椭圆
是椭圆 的两相异点,且
的两相异点,且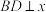 轴,求
轴,求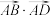 的取值范围.
的取值范围.(2)在椭圆
 的“伴随圆”上任取一点
的“伴随圆”上任取一点 ,过点
,过点 作直线
作直线 ,
, ,使得
,使得 ,
, 与椭圆
与椭圆 都只有一个交点,试判断
都只有一个交点,试判断 ,
, 是否垂直?并说明理由.
是否垂直?并说明理由.
您最近一年使用:0次
2023-03-25更新
|
819次组卷
|
5卷引用:内蒙古赤峰市八校2023届高三第三次统一模拟考试联考文科数学试题
内蒙古赤峰市八校2023届高三第三次统一模拟考试联考文科数学试题(已下线)第五篇 向量与几何 专题1 蒙日圆与阿氏圆 微点9 阿波罗尼斯圆综合训练重庆市乌江新高考协作体2023-2024学年高二下学期开学学业质量联合调研抽测数学试题2024届广东省高三毕业班综合能力测试(华娇教育摸底测试)数学试题 广东省普宁二中实验学校2023-2024学年高二下学期第一次月考数学试题
名校
解题方法
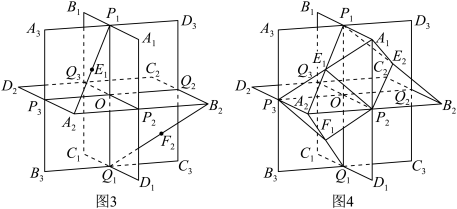
10 . 《瀑布》(图1)是最为人所知的作品之一,图中的瀑布会源源不断地落下,落下的水又逆流而上,荒唐至极,但又会让你百看不腻,画面下方还有一位饶有兴致的观察者,似乎他没发现什么不对劲.此时,他既是画外的观看者,也是埃舍尔自己.画面两座高塔各有一个几何体,左塔上方是著名的“三立方体合体”由三个正方体构成,右塔上的几何体是首次出现,后称“埃舍尔多面体”(图2)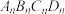 ,
,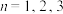 的顶点为“框架点”,定义两正方形交线为“极轴”,其端点为“极点”,记为
的顶点为“框架点”,定义两正方形交线为“极轴”,其端点为“极点”,记为 ,将极点
,将极点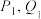 ,分别与正方形
,分别与正方形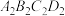 的顶点连线,取其中点记为
的顶点连线,取其中点记为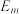 ,
,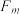 ,
,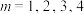 ,如(图3).埃舍尔多面体可视部分是由12个四棱锥构成,这些四棱锥顶点均为“框架点”,底面四边形由两个“极点”与两个“中点”构成,为了便于理解,图4我们构造了其中两个四棱锥
,如(图3).埃舍尔多面体可视部分是由12个四棱锥构成,这些四棱锥顶点均为“框架点”,底面四边形由两个“极点”与两个“中点”构成,为了便于理解,图4我们构造了其中两个四棱锥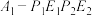 与
与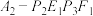
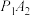 与
与 成角余弦值;
成角余弦值;
(2)求平面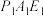 与平面
与平面 的夹角正弦值;
的夹角正弦值;
(3)求埃舍尔体的表面积与体积(直接写出答案).
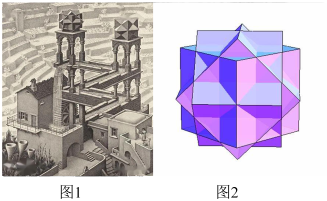
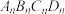 ,
,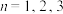 的顶点为“框架点”,定义两正方形交线为“极轴”,其端点为“极点”,记为
的顶点为“框架点”,定义两正方形交线为“极轴”,其端点为“极点”,记为 ,将极点
,将极点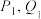 ,分别与正方形
,分别与正方形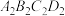 的顶点连线,取其中点记为
的顶点连线,取其中点记为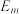 ,
,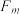 ,
,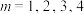 ,如(图3).埃舍尔多面体可视部分是由12个四棱锥构成,这些四棱锥顶点均为“框架点”,底面四边形由两个“极点”与两个“中点”构成,为了便于理解,图4我们构造了其中两个四棱锥
,如(图3).埃舍尔多面体可视部分是由12个四棱锥构成,这些四棱锥顶点均为“框架点”,底面四边形由两个“极点”与两个“中点”构成,为了便于理解,图4我们构造了其中两个四棱锥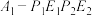 与
与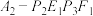
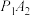 与
与 成角余弦值;
成角余弦值;(2)求平面
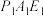 与平面
与平面 的夹角正弦值;
的夹角正弦值;(3)求埃舍尔体的表面积与体积(直接写出答案).
您最近一年使用:0次
2023-01-18更新
|
1594次组卷
|
17卷引用:上海市南洋模范中学2022-2023学年高二上学期期末数学试题
上海市南洋模范中学2022-2023学年高二上学期期末数学试题(已下线)第3章 空间向量及其应用(基础、常考、易错、压轴)分类专项训练(已下线)期末真题必刷压轴60题(23个考点专练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(人教A版2019选择性必修第一册)(已下线)期末真题必刷压轴60题(22个考点专练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(沪教版2020必修第三册)山东省青岛第五十八中学2023-2024学年高二上学期9月月考检测数学试题(已下线)压轴题立体几何新定义题(九省联考第19题模式)练重庆市缙云教育联盟2023-2024学年高二下学期2月月度质量检测数学试题(已下线)微考点8-1 新高考新题型19题新定义题型精选(已下线)第二章 立体几何中的计算 专题三 空间体积的计算 微点6 空间交叉图形公共部分体积的计算【培优版】(已下线)第六章 突破立体几何创新问题 专题一 跨学科交汇问题 微点3 跨学科交汇问题综合训练【培优版】(已下线)专题07 空间向量与立体几何(九大题型+优选提升题)-【好题汇编】备战2023-2024学年高二数学下学期期末真题分类汇编(沪教版2020选择性必修,上海专用)(已下线)上海市高二下学期期末真题必刷04(压轴题)--高二期末考点大串讲(沪教版2020选修)(已下线)重难点突破03 立体几何解答题常考模型归纳总结(九大题型)-2(已下线)专题4 立体几何中的新定义压轴大题(过关集训)福建省部分优质高中2024~2025学年高二上学期入学质量检测数学试卷山东省青岛市即墨区第一中学2024-2025学年高二上学期第一次阶段检测数学试题重庆市第七中学校2024-2025学年高二上学期第一次月考数学试卷



