2024高三·全国·专题练习
解题方法
1 . 长为3的线段 的两个端点
的两个端点 分别在
分别在 轴上移动,点
轴上移动,点 在直线
在直线 上且满足
上且满足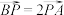 .
.
(1)求点 的轨迹方程.
的轨迹方程.
(2)记点 的轨迹为曲线
的轨迹为曲线 ,过点
,过点 任作直线
任作直线 交曲线
交曲线 于
于 两点,过
两点,过 作斜率为
作斜率为 的直线
的直线 交曲线
交曲线 于另一点
于另一点 .求证:直线
.求证:直线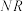 与直线
与直线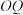 的交点为定点(
的交点为定点( 为坐标原点),并求出该定点.
为坐标原点),并求出该定点.
 的两个端点
的两个端点 分别在
分别在 轴上移动,点
轴上移动,点 在直线
在直线 上且满足
上且满足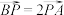 .
.(1)求点
 的轨迹方程.
的轨迹方程.(2)记点
 的轨迹为曲线
的轨迹为曲线 ,过点
,过点 任作直线
任作直线 交曲线
交曲线 于
于 两点,过
两点,过 作斜率为
作斜率为 的直线
的直线 交曲线
交曲线 于另一点
于另一点 .求证:直线
.求证:直线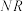 与直线
与直线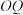 的交点为定点(
的交点为定点( 为坐标原点),并求出该定点.
为坐标原点),并求出该定点.
您最近一年使用:0次
名校
解题方法
2 . 已知结论:椭圆 上一点
上一点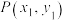 处切线方程为
处切线方程为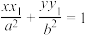 .试用此结论解答下列问题.如图,已知椭圆
.试用此结论解答下列问题.如图,已知椭圆 :
: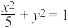 的右焦点为
的右焦点为 ,原点为
,原点为 ,椭圆的动弦AB过焦点
,椭圆的动弦AB过焦点 且不垂直于坐标轴,弦
且不垂直于坐标轴,弦 的中点为
的中点为 ,椭圆
,椭圆 在点A,B处的两切线的交点为
在点A,B处的两切线的交点为 .
.
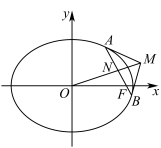
(1)试判断:O,M,N三点是否共线若三点共线,请给出证明;若三点不共线,请说明理由;
(2)求 的最小值.
的最小值.
 上一点
上一点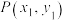 处切线方程为
处切线方程为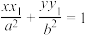 .试用此结论解答下列问题.如图,已知椭圆
.试用此结论解答下列问题.如图,已知椭圆 :
: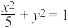 的右焦点为
的右焦点为 ,原点为
,原点为 ,椭圆的动弦AB过焦点
,椭圆的动弦AB过焦点 且不垂直于坐标轴,弦
且不垂直于坐标轴,弦 的中点为
的中点为 ,椭圆
,椭圆 在点A,B处的两切线的交点为
在点A,B处的两切线的交点为 .
.
(1)试判断:O,M,N三点是否共线若三点共线,请给出证明;若三点不共线,请说明理由;
(2)求
 的最小值.
的最小值.
您最近一年使用:0次
3 . 已知椭圆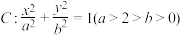 的上顶点为
的上顶点为 ,右焦点为
,右焦点为 ,原点
,原点 到直线
到直线 的距离为
的距离为 的面积为1.
的面积为1.
(1)求椭圆 的方程;
的方程;
(2)过点 的直线
的直线 与
与 交于
交于 两点,过点
两点,过点 作
作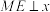 轴于点
轴于点 ,过点
,过点 作
作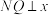 轴于点
轴于点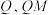 与
与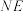 交于点
交于点 .
.
①求证:点 在定直线上,
在定直线上,
②求 的面积的最大值.
的面积的最大值.
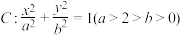 的上顶点为
的上顶点为 ,右焦点为
,右焦点为 ,原点
,原点 到直线
到直线 的距离为
的距离为 的面积为1.
的面积为1.(1)求椭圆
 的方程;
的方程;(2)过点
 的直线
的直线 与
与 交于
交于 两点,过点
两点,过点 作
作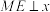 轴于点
轴于点 ,过点
,过点 作
作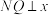 轴于点
轴于点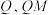 与
与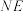 交于点
交于点 .
.①求证:点
 在定直线上,
在定直线上,②求
 的面积的最大值.
的面积的最大值.
您最近一年使用:0次
名校
解题方法
4 . 已知双曲线 的离心率为
的离心率为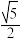 ,左、右顶点分别为
,左、右顶点分别为 ,点
,点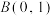 ,且
,且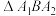 的面积为2.
的面积为2.
(1)求 的方程;
的方程;
(2)若过点 的直线
的直线 与
与 的左、右两支分别交于
的左、右两支分别交于 两点,直线
两点,直线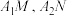 交于点
交于点 ,直线
,直线 与
与 轴交于点
轴交于点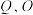 为坐标原点,证明:
为坐标原点,证明: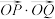 为定值.
为定值.
 的离心率为
的离心率为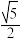 ,左、右顶点分别为
,左、右顶点分别为 ,点
,点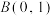 ,且
,且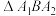 的面积为2.
的面积为2.(1)求
 的方程;
的方程;(2)若过点
 的直线
的直线 与
与 的左、右两支分别交于
的左、右两支分别交于 两点,直线
两点,直线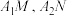 交于点
交于点 ,直线
,直线 与
与 轴交于点
轴交于点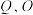 为坐标原点,证明:
为坐标原点,证明: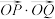 为定值.
为定值.
您最近一年使用:0次
解题方法
5 . 已知椭圆 过点
过点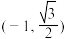 ,且离心率为
,且离心率为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)设椭圆 的左顶点为
的左顶点为 ,上顶点为
,上顶点为 ,已知直线
,已知直线 平行于直线
平行于直线 ,且交椭圆
,且交椭圆 于
于 两点,若
两点,若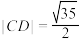 ,求直线
,求直线 的方程.
的方程.
 过点
过点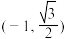 ,且离心率为
,且离心率为 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)设椭圆
 的左顶点为
的左顶点为 ,上顶点为
,上顶点为 ,已知直线
,已知直线 平行于直线
平行于直线 ,且交椭圆
,且交椭圆 于
于 两点,若
两点,若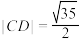 ,求直线
,求直线 的方程.
的方程.
您最近一年使用:0次
解题方法
6 . 如图,已知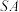 垂直于梯形
垂直于梯形 所在的平面,矩形
所在的平面,矩形 的对角线交于点
的对角线交于点 为
为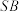 的中点,
的中点, .
.
(1)求证:
 平面
平面 ;
;
(2)在线段 上是否存在一点
上是否存在一点 ,使得
,使得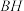 与平面
与平面 所成角的大小为
所成角的大小为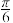 ?若存在,求出
?若存在,求出 的长;若不存在,说明理由.
的长;若不存在,说明理由.
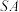 垂直于梯形
垂直于梯形 所在的平面,矩形
所在的平面,矩形 的对角线交于点
的对角线交于点 为
为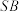 的中点,
的中点, .
.
(1)求证:

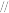 平面
平面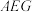 ;
;(2)在线段
 上是否存在一点
上是否存在一点 ,使得
,使得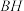 与平面
与平面 所成角的大小为
所成角的大小为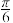 ?若存在,求出
?若存在,求出 的长;若不存在,说明理由.
的长;若不存在,说明理由.
您最近一年使用:0次
名校
解题方法
7 . 如图所示,在四棱锥 中,底面
中,底面 为直角梯形,
为直角梯形, ∥
∥ 、
、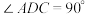 、
、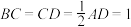 、
、 ,
, 、
、 分别为
分别为 、
、 的中点,
的中点,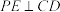 .
. 平面
平面 ;
;
(2)若 与
与 所成角为
所成角为 ,求二面角
,求二面角 的余弦值.
的余弦值.
 中,底面
中,底面 为直角梯形,
为直角梯形, ∥
∥ 、
、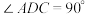 、
、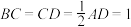 、
、 ,
, 、
、 分别为
分别为 、
、 的中点,
的中点,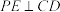 .
.
 平面
平面 ;
;(2)若
 与
与 所成角为
所成角为 ,求二面角
,求二面角 的余弦值.
的余弦值.
您最近一年使用:0次
2023-11-05更新
|
3478次组卷
|
16卷引用:新疆克拉玛依市2022届高三下学期第三次模拟检测数学(理)试题
新疆克拉玛依市2022届高三下学期第三次模拟检测数学(理)试题广东省广州市奥林匹克中学2021-2022学年高二下学期6月月考数学试题辽宁省铁岭市昌图县第一高级中学2021-2022学年高一下学期期末数学试题(已下线)1.2.4 二面角(已下线)第4讲 空间向量的应用 (3)(已下线)第07讲 空间向量的应用 (2)山西省运城市稷山县稷山中学2023-2024学年高二上学期11月月考数学试题重庆市北碚区缙云教育联盟2024届高考零诊数学试题(已下线)四川省成都市第七中学2023-2024学年高二上学期12月月考数学试题北京市丰台区2023-2024学年高二上学期期末模拟数学试题江西省上饶市广丰区南山中学2023-2024学年高二上学期期末模拟数学试题河南省郑州市第十八中学2023-2024学年高二上学期期末模拟数学试题(三)新疆维吾尔自治区阿克苏地库车市第二中学2023-2024学年高二上学期第二次月考(12月)数学黑龙江省鹤岗市萝北县高级中学2023-2024学年高一下学期7月份考试数学试题云南省大理白族自治州祥云祥华中学2023-2024学年高一下学期6月月考数学试题广东省汕尾市部分学校2023-2024学年高一下学期5月月考数学试卷
名校
解题方法
8 . 定义椭圆C: 上的点
上的点 的“圆化点”为
的“圆化点”为 .已知椭圆C的离心率为
.已知椭圆C的离心率为 ,“圆化点”D在圆
,“圆化点”D在圆 上.
上.
(1)求椭圆C的方程;
(2)设椭圆C的左顶点为A,不过点A的直线l交椭圆C于M,N两点,点M,N的“圆化点”分别为点P,Q.记直线l,AP,AQ的斜率分别为k, ,
, ,若
,若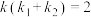 ,则直线l是否过定点?若直线l过定点,求定点的坐标;若直线l不过定点,说明理由.
,则直线l是否过定点?若直线l过定点,求定点的坐标;若直线l不过定点,说明理由.
 上的点
上的点 的“圆化点”为
的“圆化点”为 .已知椭圆C的离心率为
.已知椭圆C的离心率为 ,“圆化点”D在圆
,“圆化点”D在圆 上.
上.(1)求椭圆C的方程;
(2)设椭圆C的左顶点为A,不过点A的直线l交椭圆C于M,N两点,点M,N的“圆化点”分别为点P,Q.记直线l,AP,AQ的斜率分别为k,
 ,
, ,若
,若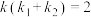 ,则直线l是否过定点?若直线l过定点,求定点的坐标;若直线l不过定点,说明理由.
,则直线l是否过定点?若直线l过定点,求定点的坐标;若直线l不过定点,说明理由.
您最近一年使用:0次
2023-03-02更新
|
852次组卷
|
4卷引用:福建省南平市2022-2023学年高二上学期期末质量检测数学试题
9 . 已知双曲线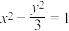 ,点A,B在双曲线右支上,O为坐标原点.
,点A,B在双曲线右支上,O为坐标原点.
(1)若过点A作双曲线的两条渐近线的平行线,分别交两条渐近线于点M,N,证明:平行四边形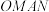 的面积为定值;
的面积为定值;
(2)若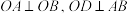 ,D为垂足,求点D的轨迹的长度.
,D为垂足,求点D的轨迹的长度.
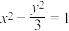 ,点A,B在双曲线右支上,O为坐标原点.
,点A,B在双曲线右支上,O为坐标原点.(1)若过点A作双曲线的两条渐近线的平行线,分别交两条渐近线于点M,N,证明:平行四边形
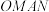 的面积为定值;
的面积为定值;(2)若
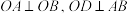 ,D为垂足,求点D的轨迹的长度.
,D为垂足,求点D的轨迹的长度.
您最近一年使用:0次
2023-02-27更新
|
549次组卷
|
3卷引用:浙江省台州市2022-2023学年高二上学期2月期末数学试题
2023高三·全国·专题练习
10 . 已知双曲线 的焦距为4,以原点为圆心,实半轴长为半径的圆和直线
的焦距为4,以原点为圆心,实半轴长为半径的圆和直线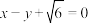 相切.
相切.
(1)求双曲线 的方程;
的方程;
(2)已知点 为双曲线
为双曲线 的左焦点,试问在
的左焦点,试问在 轴上是否存在一定点
轴上是否存在一定点 ,过点
,过点 任意作一条直线
任意作一条直线 交双曲线
交双曲线 于
于 ,
, 两点,使
两点,使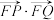 为定值?若存在,求出此定值和所有的定点
为定值?若存在,求出此定值和所有的定点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 的焦距为4,以原点为圆心,实半轴长为半径的圆和直线
的焦距为4,以原点为圆心,实半轴长为半径的圆和直线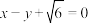 相切.
相切.(1)求双曲线
 的方程;
的方程;(2)已知点
 为双曲线
为双曲线 的左焦点,试问在
的左焦点,试问在 轴上是否存在一定点
轴上是否存在一定点 ,过点
,过点 任意作一条直线
任意作一条直线 交双曲线
交双曲线 于
于 ,
, 两点,使
两点,使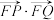 为定值?若存在,求出此定值和所有的定点
为定值?若存在,求出此定值和所有的定点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
您最近一年使用:0次
2022-11-22更新
|
1502次组卷
|
6卷引用:专题34 圆锥曲线存在性问题的探究
(已下线)专题34 圆锥曲线存在性问题的探究江西省余干中学2022-2023学年高二上学期(3—26班)第三次半月考(网课)数学试题山西大学附属中学校2022-2023学年高二上学期12月月考数学试题安徽省安庆市2023届安庆第一中学高考三模数学试题广东省梅州市五华县2023届高三上学期12月质检数学试题(已下线)专题15 圆锥曲线综合



