名校
解题方法
1 . 在棱长为2的正方体 中,
中, 为
为 的中点.
的中点. 与
与 所成角的余弦值;
所成角的余弦值;
(2)求三棱锥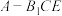 的体积.
的体积.
 中,
中, 为
为 的中点.
的中点.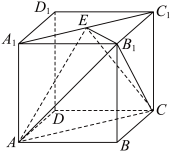
 与
与 所成角的余弦值;
所成角的余弦值;(2)求三棱锥
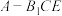 的体积.
的体积.
您最近一年使用:0次
2024-09-06更新
|
1197次组卷
|
6卷引用:广西柳州市柳城县中学等部分校联考2024-2025学年高二上学期入学检测数学试题
名校
2 . 如图(1),在 中,
中,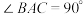 ,
,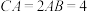 ,
, ,
, 分别是
分别是 ,
, 的中点,将
的中点,将 和
和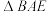 分别沿着
分别沿着 ,
, 翻折,形成三棱锥
翻折,形成三棱锥 ,
, 是
是 中点,如图(2).
中点,如图(2).
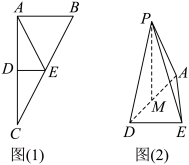
(1)求证: 平面
平面 ;
;
(2)若直线 上存在一点
上存在一点 ,使得
,使得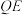 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,求
,求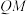 的值.
的值.
 中,
中,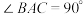 ,
,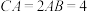 ,
, ,
, 分别是
分别是 ,
, 的中点,将
的中点,将 和
和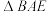 分别沿着
分别沿着 ,
, 翻折,形成三棱锥
翻折,形成三棱锥 ,
, 是
是 中点,如图(2).
中点,如图(2).
(1)求证:
 平面
平面 ;
;(2)若直线
 上存在一点
上存在一点 ,使得
,使得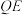 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,求
,求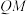 的值.
的值.
您最近一年使用:0次
2024-02-04更新
|
295次组卷
|
2卷引用:广西柳州市柳州高级中学2023-2024学年高二上学期开学考试数学试卷
名校
3 . 如图,四棱柱ABCD— 的侧棱
的侧棱 ⊥底面ABCD,四边形ABCD为菱形,E,F分别为
⊥底面ABCD,四边形ABCD为菱形,E,F分别为 ,AA1的中点.
,AA1的中点.
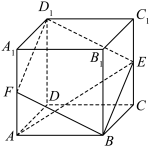
(1)证明:B,E,D1,F四点共面;
(2)若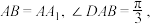 求直线AE与平面BED1F所成角的正弦值.
求直线AE与平面BED1F所成角的正弦值.
 的侧棱
的侧棱 ⊥底面ABCD,四边形ABCD为菱形,E,F分别为
⊥底面ABCD,四边形ABCD为菱形,E,F分别为 ,AA1的中点.
,AA1的中点.
(1)证明:B,E,D1,F四点共面;
(2)若
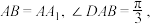 求直线AE与平面BED1F所成角的正弦值.
求直线AE与平面BED1F所成角的正弦值.
您最近一年使用:0次
2023-01-22更新
|
507次组卷
|
8卷引用:广西柳州市第三中学2023届高三下学期2月开学考数学(理)试题
广西柳州市第三中学2023届高三下学期2月开学考数学(理)试题云南省昆明市2021届“三诊一模”高三复习教学质量检测数学(理)试题(已下线)理科数学-学科网2021年高三5月大联考考后强化卷(新课标Ⅲ卷)(已下线)押第18题 立体几何-备战2021年高考数学(理)临考题号押题(全国卷1)河北省衡水市第十四中学(西校区)2021-2022学年高二上学期二调数学试题广西南宁市第二中学2023届高三上学期1月月考(期末)数学(理)试题四川省成都市成华区某重点校2023届高三阶段性考试(三)暨高考模拟考试数学(理)试题四川省德阳市第五中学2022-2023学年高二下学期6月月考数学(理)试题
名校
解题方法
4 . 如图,在多面体 中,平面
中,平面 平面
平面 ,
, ,
, ,
,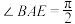 ,
,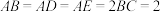 ,
, 是
是 的中点.
的中点.
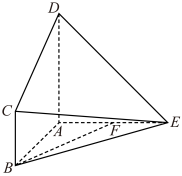
(1)证明: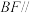 平面
平面 ;
;
(2)求点 到平面
到平面 的距离.
的距离.
 中,平面
中,平面 平面
平面 ,
, ,
, ,
,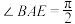 ,
,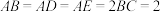 ,
, 是
是 的中点.
的中点.
(1)证明:
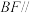 平面
平面 ;
;(2)求点
 到平面
到平面 的距离.
的距离.
您最近一年使用:0次
2022-12-17更新
|
843次组卷
|
7卷引用:广西柳州市第三中学2023届高三下学期2月开学考数学(文)试题
解题方法
5 . 如图,直四棱柱 中,
中,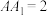 ,E为
,E为 的中点,底面
的中点,底面 是边长为4的菱形,
是边长为4的菱形,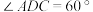 .
.
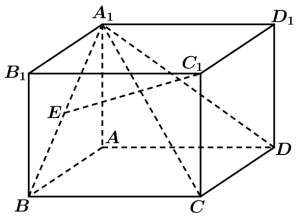
(1)证明:E, ,A,D四点共面;
,A,D四点共面;
(2)求直线 与平面
与平面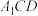 所成角的正弦值.
所成角的正弦值.
 中,
中,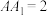 ,E为
,E为 的中点,底面
的中点,底面 是边长为4的菱形,
是边长为4的菱形,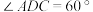 .
.
(1)证明:E,
 ,A,D四点共面;
,A,D四点共面;(2)求直线
 与平面
与平面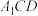 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
名校
6 . 在长方体 中,
中, ,
, ,
,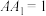 ,
, 分别为棱
分别为棱 ,
, 的中点,则异面直线
的中点,则异面直线 与
与 所成角的余弦值为
所成角的余弦值为
 中,
中, ,
, ,
,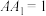 ,
, 分别为棱
分别为棱 ,
, 的中点,则异面直线
的中点,则异面直线 与
与 所成角的余弦值为
所成角的余弦值为| A.0 | B.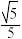 | C. | D.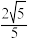 |
您最近一年使用:0次
2019-01-21更新
|
159次组卷
|
3卷引用:2020届广西柳州高级中学高三下学期开学考试数学(文)试题
7 . 如图,三棱锥 中,
中, 平面
平面
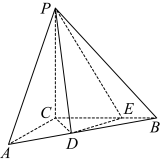
 ,
, ,
, .
. 分别为线段
分别为线段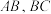 上的点,且
上的点,且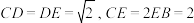 .
.
(1)证明: 平面
平面 ;
;
(2)求二面角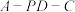 的余弦值.
的余弦值.
 中,
中, 平面
平面
 ,
, ,
, .
. 分别为线段
分别为线段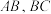 上的点,且
上的点,且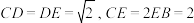 .
. (1)证明:
 平面
平面 ;
;(2)求二面角
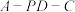 的余弦值.
的余弦值.
您最近一年使用:0次
2016-12-03更新
|
7958次组卷
|
30卷引用:2020届广西柳州高级中学高三下学期开学考试数学(理)试题
2020届广西柳州高级中学高三下学期开学考试数学(理)试题2015年全国普通高等学校招生统一考试理科数学(重庆卷)2015-2016学年吉林省扶余市一中高二上学期期末考试理科数学试卷陕西省西安市长安区第一中学2017-2018学年高二上学期第一次月考数学(重点、平行班)试题河北省阜城中学 2017-2018学年高二上学期期末考试数学试题第二章 高考链接(二)湖南省长沙市天心区长郡中学2019-2020学年高二上学期期末数学试题2020届海南省海口市海南中学高三第六次月考试卷数学广东省惠州市2020届高三上学期第一次调研数学(理)试题广东省深圳市高级中学2018-2019学年高二下学期期末数学(理)试题四川省绵阳南山中学2019-2020学年高二4月月考(学情调研)数学(理)试题山西省长治市第二中学校2019-2020学年高二下学期摸底数学(理)试题湖北省孝感市重点高中联考协作体(安陆一中、大悟一中、孝昌一中、应城一中、汉川一中)2019-2020学年高二下学期联考数学试题(已下线)数学-6月大数据精选模拟卷02(天津卷)(满分冲刺篇)湖南省娄底市2019-2020学年高二下学期期末数学试题福建省厦门第一中学2020-2021学年高三12月月考数学试题(已下线)重组卷02-冲刺2021年高考数学之精选真题+模拟重组卷(新高考地区专用)内蒙古通辽实验中学2020-2021学年高二上学期自主检测数学理科(普通班)试题云南省昆明市外国语学校2020-2021学年高二4月月考数学(理)试题福建省福州黎明中学2021-2022学年高二上学期期中考数学试题湖南省衡阳市衡阳县第四中学2022-2023学年高二上学期期中数学试题B湖北省十堰市天河英才高中2022-2023学年高二上学期期中数学试题湖南省岳阳市第五中学2022-2023学年高三上学期第四次月考数学试题湖南省邵阳市邵东创新实验学校2024届高三上学期第二次月考数学试题陕西省咸阳彩虹中学2024届高三五模理科数学试题重庆市第七中学校2023-2024学年高二上学期第四次月考数学试题(已下线)期中真题必刷压轴60题(18个考点专练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(人教A版2019选择性必修第一册)(已下线)专题23 立体几何解答题(理科)-2专题31立体几何与空间向量解答题(第二部分)河北省衡水市武强中学2024-2025学年高二上学期期中考试数学试题



