名校
1 . 某研究团队需要研究成分S的性质,以研制一种新药.现有 瓶待测试剂,这些试剂中的部分含有少量成分S,为了更方便的检测出含有成分S的待测试剂,该团队设计了以下两个方案:
瓶待测试剂,这些试剂中的部分含有少量成分S,为了更方便的检测出含有成分S的待测试剂,该团队设计了以下两个方案:
方案一:对这n瓶待测试剂进行逐一检测;
方案二:将这n瓶待测试剂分成k个小组(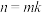 ,
,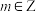 ),每个小组分别将该组的待测试剂混合后检测一次,若未检测出成分S,则不再进行检测,若检测出成分S,则对该小组的待测试剂进行逐一检测.
),每个小组分别将该组的待测试剂混合后检测一次,若未检测出成分S,则不再进行检测,若检测出成分S,则对该小组的待测试剂进行逐一检测.
已知每瓶待测试剂中含有成分S的概率均为p,设X为方案二某小组的检测次数, 为方案二的检测次数的数学期望.
为方案二的检测次数的数学期望.
(1)记 的最大值为E,求证:
的最大值为E,求证: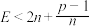 ;
;
(2)能否认为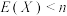 恒成立?说明理由,并以此说明方案二的合理性;
恒成立?说明理由,并以此说明方案二的合理性;
(3)给出一个能有效减少检测次数的方案,说明理由.
 瓶待测试剂,这些试剂中的部分含有少量成分S,为了更方便的检测出含有成分S的待测试剂,该团队设计了以下两个方案:
瓶待测试剂,这些试剂中的部分含有少量成分S,为了更方便的检测出含有成分S的待测试剂,该团队设计了以下两个方案:方案一:对这n瓶待测试剂进行逐一检测;
方案二:将这n瓶待测试剂分成k个小组(
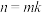 ,
,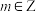 ),每个小组分别将该组的待测试剂混合后检测一次,若未检测出成分S,则不再进行检测,若检测出成分S,则对该小组的待测试剂进行逐一检测.
),每个小组分别将该组的待测试剂混合后检测一次,若未检测出成分S,则不再进行检测,若检测出成分S,则对该小组的待测试剂进行逐一检测.已知每瓶待测试剂中含有成分S的概率均为p,设X为方案二某小组的检测次数,
 为方案二的检测次数的数学期望.
为方案二的检测次数的数学期望.(1)记
 的最大值为E,求证:
的最大值为E,求证: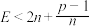 ;
;(2)能否认为
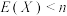 恒成立?说明理由,并以此说明方案二的合理性;
恒成立?说明理由,并以此说明方案二的合理性;(3)给出一个能有效减少检测次数的方案,说明理由.
您最近一年使用:0次
名校
2 . 芯片时常制造在半导体晶元表面上.某企业使用新技术对某款芯片制造工艺进行改进.部分芯片由智能检测系统进行筛选,其中部分次品芯片会被淘汰,筛选后的芯片及未经筛选的芯片进入流水线由工人进行抽样检验.记A表示事件“某芯片通过智能检测系统筛选”,B表示事件“某芯片经人工抽检后合格”.改进生产工艺后,这款芯片的某项质量指标 服从正态分布
服从正态分布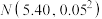 ,现从中随机抽取M个,这M个芯片中恰有m个的质量指标
,现从中随机抽取M个,这M个芯片中恰有m个的质量指标 位于区间
位于区间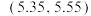 ,则下列说法正确的是( )(参考数据:
,则下列说法正确的是( )(参考数据: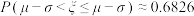 ,
,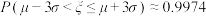 )
)
 服从正态分布
服从正态分布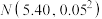 ,现从中随机抽取M个,这M个芯片中恰有m个的质量指标
,现从中随机抽取M个,这M个芯片中恰有m个的质量指标 位于区间
位于区间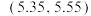 ,则下列说法正确的是( )(参考数据:
,则下列说法正确的是( )(参考数据: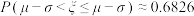 ,
,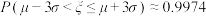 )
)A.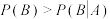 |
B.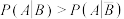 |
C.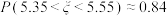 |
D. 取得最大值时,M的估计值为54 取得最大值时,M的估计值为54 |
您最近一年使用:0次
解题方法
3 . 如图:一张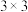 的棋盘,横行编号
的棋盘,横行编号 :竖排编号
:竖排编号 .一颗棋子目前位于棋盘的
.一颗棋子目前位于棋盘的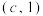 处,它的移动规则是:每次移动到与自身所在格不相邻的异色格中.例如该棋子第一次移动可以从
处,它的移动规则是:每次移动到与自身所在格不相邻的异色格中.例如该棋子第一次移动可以从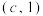 移动到
移动到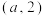 或
或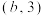 .棋子每次移动到不同目的地间的概率均为
.棋子每次移动到不同目的地间的概率均为 .
.
②假设棋子两次移动后,最终停留到第1,2,3行时,分别能获得 分,设得分为
分,设得分为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(2)现在于棋盘左下角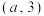 处加入一颗棋子,他们运动规则相同,并且每次移动同时行动.移动
处加入一颗棋子,他们运动规则相同,并且每次移动同时行动.移动 次后,两棋子位于同一格的概率为
次后,两棋子位于同一格的概率为 ,求
,求 的通项公式.
的通项公式.
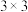 的棋盘,横行编号
的棋盘,横行编号 :竖排编号
:竖排编号 .一颗棋子目前位于棋盘的
.一颗棋子目前位于棋盘的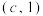 处,它的移动规则是:每次移动到与自身所在格不相邻的异色格中.例如该棋子第一次移动可以从
处,它的移动规则是:每次移动到与自身所在格不相邻的异色格中.例如该棋子第一次移动可以从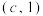 移动到
移动到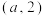 或
或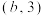 .棋子每次移动到不同目的地间的概率均为
.棋子每次移动到不同目的地间的概率均为 .
.
②假设棋子两次移动后,最终停留到第1,2,3行时,分别能获得
 分,设得分为
分,设得分为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.(2)现在于棋盘左下角
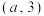 处加入一颗棋子,他们运动规则相同,并且每次移动同时行动.移动
处加入一颗棋子,他们运动规则相同,并且每次移动同时行动.移动 次后,两棋子位于同一格的概率为
次后,两棋子位于同一格的概率为 ,求
,求 的通项公式.
的通项公式.
您最近一年使用:0次
4 . 已知 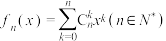 .
.
(1)若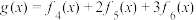 ,求
,求 中含
中含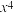 项的系数;
项的系数;
(2)证明: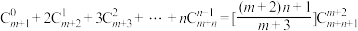 .
.
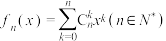 .
.(1)若
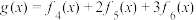 ,求
,求 中含
中含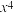 项的系数;
项的系数;(2)证明:
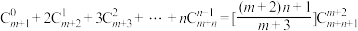 .
.
您最近一年使用:0次
5 . 马尔科夫链是概率统计中的一个重要模型,其过程具备“无记忆”的性质:下一状态的概率分布只能由当前状态决定,即第n+1次状态的概率分布只与第n次的状态有关,与第 ,…次的状态无关,即
,…次的状态无关,即 .已知甲盒中装有1个白球和2个黑球,乙盒中装有2个白球,现从甲、乙两个盒中各任取1个球交换放入对方的盒中,重复n次(
.已知甲盒中装有1个白球和2个黑球,乙盒中装有2个白球,现从甲、乙两个盒中各任取1个球交换放入对方的盒中,重复n次( )这样的操作,记此时甲盒中白球的个数为
)这样的操作,记此时甲盒中白球的个数为 ,甲盒中恰有2个白球的概率为
,甲盒中恰有2个白球的概率为 ,恰有1个白球的概率为
,恰有1个白球的概率为 .
.
(1)求 和
和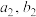 .
.
(2)证明: 为等比数列.
为等比数列.
(3)求 的数学期望(用n表示).
的数学期望(用n表示).
 ,…次的状态无关,即
,…次的状态无关,即 .已知甲盒中装有1个白球和2个黑球,乙盒中装有2个白球,现从甲、乙两个盒中各任取1个球交换放入对方的盒中,重复n次(
.已知甲盒中装有1个白球和2个黑球,乙盒中装有2个白球,现从甲、乙两个盒中各任取1个球交换放入对方的盒中,重复n次( )这样的操作,记此时甲盒中白球的个数为
)这样的操作,记此时甲盒中白球的个数为 ,甲盒中恰有2个白球的概率为
,甲盒中恰有2个白球的概率为 ,恰有1个白球的概率为
,恰有1个白球的概率为 .
.(1)求
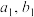 和
和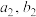 .
.(2)证明:
 为等比数列.
为等比数列.(3)求
 的数学期望(用n表示).
的数学期望(用n表示).
您最近一年使用:0次
2024-09-02更新
|
296次组卷
|
4卷引用:重难点突破03 高等背景下概率论新定义(七大题型)
(已下线)重难点突破03 高等背景下概率论新定义(七大题型)(已下线)重难点突破01 概率与统计的综合问题(十八大题型)江西省部分学校2024-2025学年高三上学期开学第一次月考数学试卷福建省德化第二中学2024-2025学年高三上学期第一阶段考试(10月)数学试题
解题方法
6 . 设点 从格点
从格点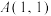 出发,沿格径以最短的路线运动到点
出发,沿格径以最短的路线运动到点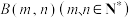 ,即每次运动到另一格点时,横坐标或纵坐标增加1.设点
,即每次运动到另一格点时,横坐标或纵坐标增加1.设点 经过的所有格点中两坐标乘积之和为
经过的所有格点中两坐标乘积之和为 .
.
(1)当 时,点
时,点 沿格径以最短的路线运动到点
沿格径以最短的路线运动到点 的方案有多少种?
的方案有多少种?
(2)当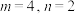 时,求
时,求 的最大值;
的最大值;
(3)当点 从格点
从格点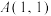 出发,沿格径以最短的路线运动到点
出发,沿格径以最短的路线运动到点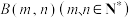 且
且 ,求
,求 的最大值.(参考公式:
的最大值.(参考公式: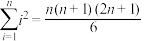 )
)
 从格点
从格点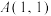 出发,沿格径以最短的路线运动到点
出发,沿格径以最短的路线运动到点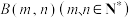 ,即每次运动到另一格点时,横坐标或纵坐标增加1.设点
,即每次运动到另一格点时,横坐标或纵坐标增加1.设点 经过的所有格点中两坐标乘积之和为
经过的所有格点中两坐标乘积之和为 .
.(1)当
 时,点
时,点 沿格径以最短的路线运动到点
沿格径以最短的路线运动到点 的方案有多少种?
的方案有多少种?(2)当
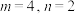 时,求
时,求 的最大值;
的最大值;(3)当点
 从格点
从格点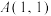 出发,沿格径以最短的路线运动到点
出发,沿格径以最短的路线运动到点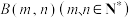 且
且 ,求
,求 的最大值.(参考公式:
的最大值.(参考公式: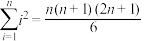 )
)
您最近一年使用:0次
解题方法
7 . 某箱中有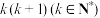 个除颜色之外均相同的球,
个除颜色之外均相同的球, 已知.箱中1个球为白球,其余为黑球.现在该箱中进行一取球实验:每次从箱中等可能地取出一个球,若取出白球或取球
已知.箱中1个球为白球,其余为黑球.现在该箱中进行一取球实验:每次从箱中等可能地取出一个球,若取出白球或取球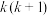 次后结束实验,否则进行相应操作进行下一次取球.设实验结束时的取球次数为
次后结束实验,否则进行相应操作进行下一次取球.设实验结束时的取球次数为 .
.
(1)若取出黑球后放回箱中,求 的数学期望
的数学期望 ;
;
(2)若取出黑球后替换为白球放回箱中,求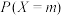 的最大值
的最大值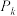 ,并证明:
,并证明: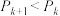 .
.
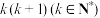 个除颜色之外均相同的球,
个除颜色之外均相同的球, 已知.箱中1个球为白球,其余为黑球.现在该箱中进行一取球实验:每次从箱中等可能地取出一个球,若取出白球或取球
已知.箱中1个球为白球,其余为黑球.现在该箱中进行一取球实验:每次从箱中等可能地取出一个球,若取出白球或取球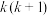 次后结束实验,否则进行相应操作进行下一次取球.设实验结束时的取球次数为
次后结束实验,否则进行相应操作进行下一次取球.设实验结束时的取球次数为 .
.(1)若取出黑球后放回箱中,求
 的数学期望
的数学期望 ;
;(2)若取出黑球后替换为白球放回箱中,求
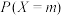 的最大值
的最大值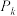 ,并证明:
,并证明: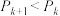 .
.
您最近一年使用:0次
8 . 将编号为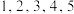 的5个小球随机放置在圆周的5个等分点上,每个等分点上各有一个小球.则使圆周上所有相邻两球号码之差的绝对值之和最小的放法的概率为
的5个小球随机放置在圆周的5个等分点上,每个等分点上各有一个小球.则使圆周上所有相邻两球号码之差的绝对值之和最小的放法的概率为__________ .
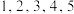 的5个小球随机放置在圆周的5个等分点上,每个等分点上各有一个小球.则使圆周上所有相邻两球号码之差的绝对值之和最小的放法的概率为
的5个小球随机放置在圆周的5个等分点上,每个等分点上各有一个小球.则使圆周上所有相邻两球号码之差的绝对值之和最小的放法的概率为
您最近一年使用:0次
9 . 设 都是不小于3的整数,当
都是不小于3的整数,当 时,
时,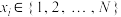 ,设集合
,设集合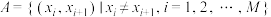 ,如果
,如果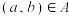 与
与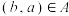 不能同时成立,则( )
不能同时成立,则( )
 都是不小于3的整数,当
都是不小于3的整数,当 时,
时,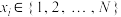 ,设集合
,设集合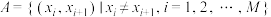 ,如果
,如果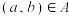 与
与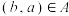 不能同时成立,则( )
不能同时成立,则( )A.若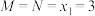 ,则 ,则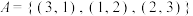 或 或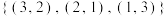 |
B.若 ,则 ,则 的可能取值为3或4或5 的可能取值为3或4或5 |
C.若 的值确定,则 的值确定,则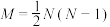 |
D.若 为奇数,则 为奇数,则 的最大值为 的最大值为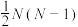 |
您最近一年使用:0次
10 . (1)我们学过组合恒等式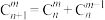 ,实际上可以理解为
,实际上可以理解为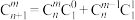 ,请你利用这个观点快速求解:
,请你利用这个观点快速求解: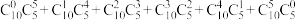 .(计算结果用组合数表示)
.(计算结果用组合数表示)
(2)(i)求证: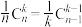 ;
;
(ii)求值: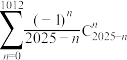 .
.
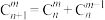 ,实际上可以理解为
,实际上可以理解为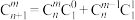 ,请你利用这个观点快速求解:
,请你利用这个观点快速求解: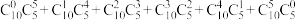 .(计算结果用组合数表示)
.(计算结果用组合数表示)(2)(i)求证:
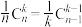 ;
;(ii)求值:
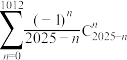 .
.
您最近一年使用:0次



