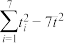2023高三上·全国·专题练习
名校
1 . 数独是源自18世纪瑞士的一种数学游戏,玩家需要根据 盘面上的已知数字,推理出所有剩余空格的数字,并满足每一行、每一列、每一个粗线宫(
盘面上的已知数字,推理出所有剩余空格的数字,并满足每一行、每一列、每一个粗线宫(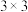 )内的数字均含1~9,且不重复.数独爱好者小明打算报名参加“丝路杯”全国数独大赛初级组的比赛.
)内的数字均含1~9,且不重复.数独爱好者小明打算报名参加“丝路杯”全国数独大赛初级组的比赛.
参考数据:
参考公式:对于一组数据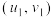 ,
,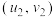 ,⋯,
,⋯,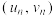 ,其经验回归方程
,其经验回归方程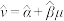 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为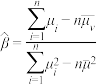 ,
,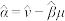 .
.
(1)赛前小明进行了一段时间的训练,每天解题的平均速度y(秒/题)与训练天数x(天)有关,经统计得到如下数据:
现用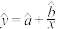 作为回归方程模型,请利用表中数据,求出该回归方程;(用分数表示)
作为回归方程模型,请利用表中数据,求出该回归方程;(用分数表示)
(2)小明和小红玩“对战赛”,每局两人同时开始解一道数独题,先解出题的人获胜,不存在平局,两人约定先胜3局者赢得比赛.若小明每局获胜的概率为 ,且各局之间相互独立,设比赛X局后结束,求随机变量X的分布列及均值.
,且各局之间相互独立,设比赛X局后结束,求随机变量X的分布列及均值.
 盘面上的已知数字,推理出所有剩余空格的数字,并满足每一行、每一列、每一个粗线宫(
盘面上的已知数字,推理出所有剩余空格的数字,并满足每一行、每一列、每一个粗线宫(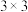 )内的数字均含1~9,且不重复.数独爱好者小明打算报名参加“丝路杯”全国数独大赛初级组的比赛.
)内的数字均含1~9,且不重复.数独爱好者小明打算报名参加“丝路杯”全国数独大赛初级组的比赛.参考数据:

|
|
|
1750 | 0.37 | 0.55 |
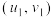 ,
,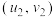 ,⋯,
,⋯,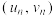 ,其经验回归方程
,其经验回归方程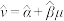 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,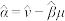 .
.(1)赛前小明进行了一段时间的训练,每天解题的平均速度y(秒/题)与训练天数x(天)有关,经统计得到如下数据:
x(天) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
y(秒/题) | 910 | 800 | 600 | 440 | 300 | 240 | 210 |
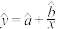 作为回归方程模型,请利用表中数据,求出该回归方程;(用分数表示)
作为回归方程模型,请利用表中数据,求出该回归方程;(用分数表示)(2)小明和小红玩“对战赛”,每局两人同时开始解一道数独题,先解出题的人获胜,不存在平局,两人约定先胜3局者赢得比赛.若小明每局获胜的概率为
 ,且各局之间相互独立,设比赛X局后结束,求随机变量X的分布列及均值.
,且各局之间相互独立,设比赛X局后结束,求随机变量X的分布列及均值.
您最近一年使用:0次
2024-10-24更新
|
188次组卷
|
13卷引用:第9章 统计 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
(已下线)第9章 统计 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)9.1 线性回归分析(2)(已下线)第九章 重难专攻(十二)概率中的综合题 核心考点集训 一轮点点通(已下线)专题21 概率与统计的综合运用(13大题型)(练习)(已下线)专题3 变量的相关性、回归分析压轴大题【讲】(已下线)第四章 统计 专题二 统计相关性与回归分析 微点2 相关分析与回归分析(二)【培优版】(已下线)第五章 概率统计创新问题 专题五 概率统计中的数学文化 微点3 概率统计中的数学文化综合训练【基础版】(已下线)第五章 概率统计创新问题 专题六 概率统计中的数学文化 微点2 概率统计与数学文化的交汇(二)【培优版】山东省潍坊市昌乐第一中学2024届高三上学期12月月考数学试题(已下线)4.3.1 一元线性回归模型线(分层练习)-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第二册)(已下线)第04讲 拓展一:数学建模 建立统计模型进行预测(非线性回归模型)-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)内蒙古呼和浩特市回民区2023-2024学年高二下学期期中考试数学试题山东省青岛第五十八中学2023-2024学年高二下学期期中数学试题
名校
2 . 在一场羽毛球比赛中,甲、乙、丙、丁四人角逐冠军. 比赛采用“双败淘汰制”:首先,四人通过抽签分成两组,每组中的两人对阵,每组的胜者进入“胜区”,败者进入“败区”. 接着,“胜区”中两人对阵,胜者进入“决赛区”;“败区”中两人对阵,败者直接淘汰出局获第四名. 然后,“败区”的胜者和“胜区”的败者对阵,胜者进入“决赛区”,败者获第三名. 最后,“决赛区”的两人进行冠军决赛,胜者获得冠军,败者获第二名. 已知甲对阵乙、丙、丁获胜的概率均为p( ),且不同对阵的结果相互独立.
),且不同对阵的结果相互独立.
(1)若 ,经抽签,第一轮由甲对阵乙,丙对阵丁;
,经抽签,第一轮由甲对阵乙,丙对阵丁;
①求甲获得第四名的概率;
②求甲在“双败淘汰制”下参与对阵的比赛场数的数学期望;
(2)除“双败淘汰制”外,也经常采用“单败淘汰制”:四人通过抽签分成两组,每组中的两人对阵,每组的胜者进入“决赛区”,败者淘汰;最后,“决赛区”的两人进行冠军决赛,胜者获得冠军. 已知甲对阵乙、丙、丁获胜的概率均为p( ),则哪种赛制对甲夺冠有利?请说明理由.
),则哪种赛制对甲夺冠有利?请说明理由.
 ),且不同对阵的结果相互独立.
),且不同对阵的结果相互独立.(1)若
 ,经抽签,第一轮由甲对阵乙,丙对阵丁;
,经抽签,第一轮由甲对阵乙,丙对阵丁; ①求甲获得第四名的概率;
②求甲在“双败淘汰制”下参与对阵的比赛场数的数学期望;
(2)除“双败淘汰制”外,也经常采用“单败淘汰制”:四人通过抽签分成两组,每组中的两人对阵,每组的胜者进入“决赛区”,败者淘汰;最后,“决赛区”的两人进行冠军决赛,胜者获得冠军. 已知甲对阵乙、丙、丁获胜的概率均为p(
 ),则哪种赛制对甲夺冠有利?请说明理由.
),则哪种赛制对甲夺冠有利?请说明理由.
您最近一年使用:0次
2024-09-18更新
|
472次组卷
|
2卷引用:江苏省镇江市2024届高三下学期高考前练习(三模)数学试题
名校
3 . 投掷一枚骰子,向上点数共有1-6六种可能,每一种情况的发生是等可能的,则下列说法正确的是( )
| A.事件A“点数为1或2”和事件B“点数为偶数”是相互独立事件; |
| B.每一局投两次,记较大点数为该局得分,则每局得分的数学期望为4; |
| C.事件C“点数为1或2或3”和事件B“点数为偶数”是相互独立事件; |
D.连续投掷40次,记出现6点的次数 ,则随机变量 ,则随机变量 的分布列中, 的分布列中, 时概率最大. 时概率最大. |
您最近一年使用:0次
2024-09-08更新
|
192次组卷
|
3卷引用:江苏省徐州市第三中学2024届高三迎一检复习数学试题(四)
江苏省徐州市第三中学2024届高三迎一检复习数学试题(四)(已下线)第三章 随机变量及其分布列 专题三 重要的概率分布模型 微点5 重要的概率分布模型综合训练【培优版】江西省上饶市广丰一中2025届高三上学期第一次自测数学试题
解题方法
4 . 人民网2023年4月21日消息:美国时间4月20日,美国太空探索技术公司(SpaceⅩ)“星舟”(Starship)重型运载火箭在得克萨斯州首次试验发射,但火箭升空后不久爆炸.该火箭的一级助推器配备了33台发动机,但现场画面显示,火箭升空后,有8台发动机并未喷出火焰或推力出现严重不足.若一火箭内有功能、形状完全相同的33台发动机,恰有8台有故障,现准备随机不放回地每次抽取一台发动机进行验证检查,直至将8台故障发动机查出时停止检查,且故障发动机必须全部经过检查.
(1)求共抽取32台发动机就完成整个检查的概率;
(2)①证明: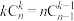 ;
;
②记总的检查次数为 ,求
,求 并化简结果.
并化简结果.
(1)求共抽取32台发动机就完成整个检查的概率;
(2)①证明:
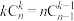 ;
;②记总的检查次数为
 ,求
,求 并化简结果.
并化简结果.
您最近一年使用:0次
5 . 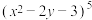 的展开式中
的展开式中 项的系数为
项的系数为________ .
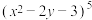 的展开式中
的展开式中 项的系数为
项的系数为
您最近一年使用:0次
解题方法
6 . 同时投掷甲、乙两枚质地均匀的硬币,记“甲正面向上”为事件 ,“乙正面向上”为事件
,“乙正面向上”为事件 ,“甲、乙至少一枚正面向上”为事件
,“甲、乙至少一枚正面向上”为事件 ,则下列判断正确的是( )
,则下列判断正确的是( )
 ,“乙正面向上”为事件
,“乙正面向上”为事件 ,“甲、乙至少一枚正面向上”为事件
,“甲、乙至少一枚正面向上”为事件 ,则下列判断正确的是( )
,则下列判断正确的是( )A. 与 与 相互对立 相互对立 | B. 与 与 相互独立 相互独立 |
C.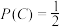 | D.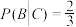 |
您最近一年使用:0次
名校
7 . 高三开学,学校举办运动会,女子啦啦队排成一排坐在跑道外侧.因烈日暴晒,每个班的啦啦队两侧已经摆好了两个遮阳伞,但每个遮阳伞的荫蔽半径仅为一名同学,为了效益最佳,遮阳伞的摆放遵循伞与伞之间至少要有一名同学的规则.高三(一)班共有七名女生现在正坐成一排,因两边的遮阳伞荫蔽范围太小,现在考虑在她们中间添置三个遮阳伞.则添置遮阳伞后,晒黑女生人数的数学期望为___________
您最近一年使用:0次
2024-09-02更新
|
200次组卷
|
4卷引用:江苏省苏州市部分学校2025届高三7月适应性模拟演练数学试题
江苏省苏州市部分学校2025届高三7月适应性模拟演练数学试题(已下线)专题7 期望方差 定义性质(经典好题母题)【练】(已下线)第十章 计数原理、概率、随机变量及其分布(测试)河南省驻马店市新蔡县第一高级中学2025届高三上学期9月月考数学试题
8 . 为推进乡村振兴计划,某镇通过实地考察当地状况,大力推广当地特色农产品.为了统计甲村,乙村生产该产品的质量,现对甲乙两村各随机选取300件产品,产品的质量如下:
(1)分析能否有 的把握认为甲乙两村的产品质量有差异?
的把握认为甲乙两村的产品质量有差异?
(2)该镇通过线上平台对乡村生产的产品进行售卖,经统计,该产品在 年上半年的月销量符合正态分布
年上半年的月销量符合正态分布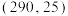 ,乡镇人员现从
,乡镇人员现从 年的前
年的前 个月中随机选取三个月的销量数据,其中销量数据不低于
个月中随机选取三个月的销量数据,其中销量数据不低于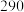 的记为
的记为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.
附: ,
,
| 合格 | 不合格 | 合计 | |
| 甲村 | 270 | 30 | 300 |
| 乙村 | 290 | 10 | 300 |
| 合计 | 560 | 40 | 600 |
 的把握认为甲乙两村的产品质量有差异?
的把握认为甲乙两村的产品质量有差异?(2)该镇通过线上平台对乡村生产的产品进行售卖,经统计,该产品在
 年上半年的月销量符合正态分布
年上半年的月销量符合正态分布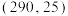 ,乡镇人员现从
,乡镇人员现从 年的前
年的前 个月中随机选取三个月的销量数据,其中销量数据不低于
个月中随机选取三个月的销量数据,其中销量数据不低于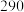 的记为
的记为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.附:
 ,
,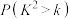 | 0.1 | 0.05 | 0.01 |
| k | 2.706 | 3.841 | 6.635 |
您最近一年使用:0次
9 . 已知一正五棱锥,其顶点与各侧棱中点合计11个点.从这11个点中任选4个点,这四个点不共面的概率为______
您最近一年使用:0次
10 . 二项式 中展开式中
中展开式中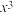 项的系数为
项的系数为______
 中展开式中
中展开式中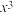 项的系数为
项的系数为
您最近一年使用:0次