1 . 已知 :
: 为有穷数列.若对任意的
为有穷数列.若对任意的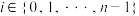 ,都有
,都有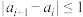 (规定
(规定 ),则称
),则称 具有性质
具有性质 .设
.设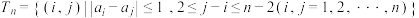 .
.
(1)判断数列 :1,0.1,-0.2,0.5,
:1,0.1,-0.2,0.5, :1,2,0.7,1.2,2是否具有性质P?若具有性质P,写出对应的集合
:1,2,0.7,1.2,2是否具有性质P?若具有性质P,写出对应的集合 ;
;
(2)若 具有性质
具有性质 ,证明:
,证明: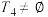 ;
;
(3)给定正整数 ,对所有具有性质
,对所有具有性质 的数列
的数列 ,求
,求 中元素个数的最小值.
中元素个数的最小值.
 :
: 为有穷数列.若对任意的
为有穷数列.若对任意的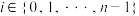 ,都有
,都有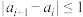 (规定
(规定 ),则称
),则称 具有性质
具有性质 .设
.设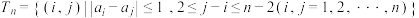 .
.(1)判断数列
 :1,0.1,-0.2,0.5,
:1,0.1,-0.2,0.5, :1,2,0.7,1.2,2是否具有性质P?若具有性质P,写出对应的集合
:1,2,0.7,1.2,2是否具有性质P?若具有性质P,写出对应的集合 ;
;(2)若
 具有性质
具有性质 ,证明:
,证明: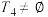 ;
;(3)给定正整数
 ,对所有具有性质
,对所有具有性质 的数列
的数列 ,求
,求 中元素个数的最小值.
中元素个数的最小值.
您最近半年使用:0次
2023-11-02更新
|
421次组卷
|
2卷引用:北京一零一中2023-2024学年高二上学期期中考试数学试题
名校
2 . 已知由实数组成的数组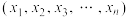 满足下面两个条件:
满足下面两个条件:
① ;②
;② .
.
(1)当 时,求
时,求 ,
, 的值;
的值;
(2)当 时,求证
时,求证 ;
;
(3)设 ,且
,且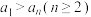 ,求证:
,求证: .
.
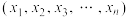 满足下面两个条件:
满足下面两个条件:①
 ;②
;② .
.(1)当
 时,求
时,求 ,
, 的值;
的值;(2)当
 时,求证
时,求证 ;
;(3)设
 ,且
,且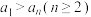 ,求证:
,求证: .
.
您最近半年使用:0次
真题
名校
3 . 给定有限个正数满足条件T:每个数都不大于50且总和 .现将这些数按下列要求进行分组,每组数之和不大于150且分组的步骤是:首先,从这些数中选择这样一些数构成第一组,使得150与这组数之和的差
.现将这些数按下列要求进行分组,每组数之和不大于150且分组的步骤是:首先,从这些数中选择这样一些数构成第一组,使得150与这组数之和的差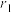 与所有可能的其他选择相比是最小的,
与所有可能的其他选择相比是最小的,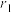 称为第一组余差;然后,在去掉已选入第一组的数后,对余下的数按第一组的选择方式构成第二组,这时的余差为
称为第一组余差;然后,在去掉已选入第一组的数后,对余下的数按第一组的选择方式构成第二组,这时的余差为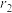 ;如此继续构成第三组(余差为
;如此继续构成第三组(余差为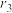 )、第四组(余差为
)、第四组(余差为 )、…,直至第N组(余差为
)、…,直至第N组(余差为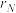 )把这些数全部分完为止.
)把这些数全部分完为止.
(1)判断,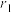 ,
,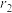 …
…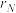 的大小关系,并指出除第N组外的每组至少含有几个数;
的大小关系,并指出除第N组外的每组至少含有几个数;
(2)当构成第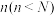 组后,指出余下的每个数与
组后,指出余下的每个数与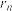 的大小关系,并证
的大小关系,并证 ;
;
(3)对任何满足条件T的有限个正数,证明: .
.
 .现将这些数按下列要求进行分组,每组数之和不大于150且分组的步骤是:首先,从这些数中选择这样一些数构成第一组,使得150与这组数之和的差
.现将这些数按下列要求进行分组,每组数之和不大于150且分组的步骤是:首先,从这些数中选择这样一些数构成第一组,使得150与这组数之和的差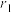 与所有可能的其他选择相比是最小的,
与所有可能的其他选择相比是最小的,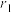 称为第一组余差;然后,在去掉已选入第一组的数后,对余下的数按第一组的选择方式构成第二组,这时的余差为
称为第一组余差;然后,在去掉已选入第一组的数后,对余下的数按第一组的选择方式构成第二组,这时的余差为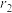 ;如此继续构成第三组(余差为
;如此继续构成第三组(余差为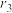 )、第四组(余差为
)、第四组(余差为 )、…,直至第N组(余差为
)、…,直至第N组(余差为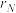 )把这些数全部分完为止.
)把这些数全部分完为止.(1)判断,
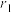 ,
,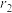 …
…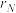 的大小关系,并指出除第N组外的每组至少含有几个数;
的大小关系,并指出除第N组外的每组至少含有几个数;(2)当构成第
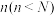 组后,指出余下的每个数与
组后,指出余下的每个数与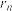 的大小关系,并证
的大小关系,并证 ;
;(3)对任何满足条件T的有限个正数,证明:
 .
.
您最近半年使用:0次
2020-12-03更新
|
546次组卷
|
5卷引用:2004 年普通高等学校招生考试数学(理)试题(北京卷)
2004 年普通高等学校招生考试数学(理)试题(北京卷)2004 年普通高等学校招生考试数学(文)试题(北京卷)上海市虹口区复兴高级中学2020-2021学年高一上学期期中数学试题(已下线)上海高一上学期期中【压轴42题专练】(2)(已下线)第六篇 数论 专题1 数论中的特殊数 微点1 数论中的特殊数
4 . 已知集合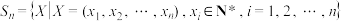 (
( ).对于
).对于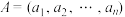 ,
,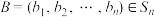 ,定义
,定义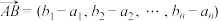 ;
; (
(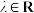 );
); 与
与 之间的距离为
之间的距离为 .
.
(Ⅰ)当 时,设
时,设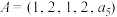 ,
, .若
.若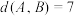 ,求
,求 ;
;
(Ⅱ)(ⅰ)证明:若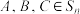 ,且
,且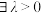 ,使
,使 ,则
,则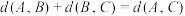 ;
;
(ⅱ)设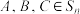 ,且
,且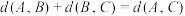 .是否一定
.是否一定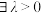 ,使
,使 ?说明理由;
?说明理由;
(Ⅲ)记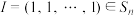 .若
.若 ,
,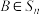 ,且
,且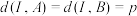 ,求
,求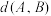 的最大值.
的最大值.
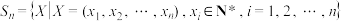 (
( ).对于
).对于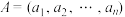 ,
,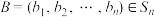 ,定义
,定义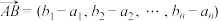 ;
; (
(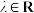 );
); 与
与 之间的距离为
之间的距离为 .
.(Ⅰ)当
 时,设
时,设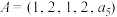 ,
, .若
.若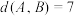 ,求
,求 ;
;(Ⅱ)(ⅰ)证明:若
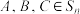 ,且
,且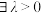 ,使
,使 ,则
,则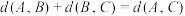 ;
; (ⅱ)设
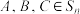 ,且
,且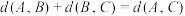 .是否一定
.是否一定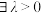 ,使
,使 ?说明理由;
?说明理由;(Ⅲ)记
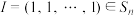 .若
.若 ,
,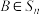 ,且
,且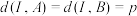 ,求
,求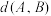 的最大值.
的最大值.
您最近半年使用:0次
2020-05-19更新
|
890次组卷
|
4卷引用:2020届北京市第四中学高三第二学期数学统练1试题
2020届北京市第四中学高三第二学期数学统练1试题北京市第二中学2020~2021学年高一下学期第四学段考试数学试题北京市第二中学2021-2022学年高一下学期第四学段考试数学试题(已下线)重难点01平面向量的实际应用与新定义(3)
18-19高三下·江苏·阶段练习
名校
解题方法
5 . 如果数列 满足“对任意正整数i,j,
满足“对任意正整数i,j,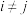 ,都存在正整数k,使得
,都存在正整数k,使得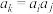 ”,则称数列
”,则称数列 具有“性质P”.已知数列是无穷项的等差数列,公差为d.
具有“性质P”.已知数列是无穷项的等差数列,公差为d.
(1)若 ,
, ,判断数列
,判断数列 是否具有“性质P”,并说明理由;
是否具有“性质P”,并说明理由;
(2)若数列 具有“性质P”,求证:
具有“性质P”,求证: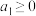 且
且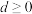 ;
;
(3)若数列 具有“性质P”,且存在正整数k,使得
具有“性质P”,且存在正整数k,使得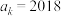 ,这样的数列共有多少个?并说明理由.
,这样的数列共有多少个?并说明理由.
 满足“对任意正整数i,j,
满足“对任意正整数i,j,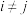 ,都存在正整数k,使得
,都存在正整数k,使得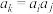 ”,则称数列
”,则称数列 具有“性质P”.已知数列是无穷项的等差数列,公差为d.
具有“性质P”.已知数列是无穷项的等差数列,公差为d.(1)若
 ,
, ,判断数列
,判断数列 是否具有“性质P”,并说明理由;
是否具有“性质P”,并说明理由;(2)若数列
 具有“性质P”,求证:
具有“性质P”,求证: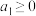 且
且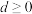 ;
;(3)若数列
 具有“性质P”,且存在正整数k,使得
具有“性质P”,且存在正整数k,使得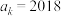 ,这样的数列共有多少个?并说明理由.
,这样的数列共有多少个?并说明理由.
您最近半年使用:0次
6 . 已知集合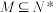 ,且
,且 中的元素个数
中的元素个数 大于等于5.若集合
大于等于5.若集合 中存在四个不同的元素
中存在四个不同的元素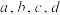 ,使得
,使得 ,则称集合
,则称集合 是“关联的”,并称集合
是“关联的”,并称集合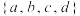 是集合
是集合 的“关联子集”;若集合
的“关联子集”;若集合 不存在“关联子集”,则称集合
不存在“关联子集”,则称集合 是“独立的”.
是“独立的”.
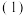 分别判断集合
分别判断集合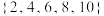 和集合
和集合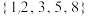 是“关联的”还是“独立的”?若是“关联的”,写出其
是“关联的”还是“独立的”?若是“关联的”,写出其所有 的关联子集;
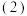 已知集合
已知集合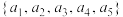 是“关联的”,且任取集合
是“关联的”,且任取集合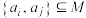 ,总存在
,总存在 的关联子集
的关联子集 ,使得
,使得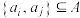 .若
.若 ,求证:
,求证: 是等差数列;
是等差数列;
 集合
集合 是“独立的”,求证:存在
是“独立的”,求证:存在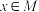 ,使得
,使得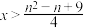 .
.
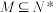 ,且
,且 中的元素个数
中的元素个数 大于等于5.若集合
大于等于5.若集合 中存在四个不同的元素
中存在四个不同的元素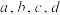 ,使得
,使得 ,则称集合
,则称集合 是“关联的”,并称集合
是“关联的”,并称集合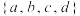 是集合
是集合 的“关联子集”;若集合
的“关联子集”;若集合 不存在“关联子集”,则称集合
不存在“关联子集”,则称集合 是“独立的”.
是“独立的”.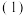 分别判断集合
分别判断集合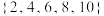 和集合
和集合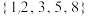 是“关联的”还是“独立的”?若是“关联的”,写出其
是“关联的”还是“独立的”?若是“关联的”,写出其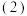 已知集合
已知集合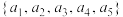 是“关联的”,且任取集合
是“关联的”,且任取集合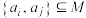 ,总存在
,总存在 的关联子集
的关联子集 ,使得
,使得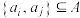 .若
.若 ,求证:
,求证: 是等差数列;
是等差数列; 集合
集合 是“独立的”,求证:存在
是“独立的”,求证:存在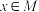 ,使得
,使得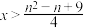 .
.
您最近半年使用:0次
2020-02-09更新
|
1496次组卷
|
9卷引用:2020届北京市海淀区高三上学期期中数学试题
2020届北京市海淀区高三上学期期中数学试题(已下线)专题02 拿高分题目强化卷(第三篇)-备战2021年新高考数学分层强化训练(北京专版)北京市海淀区2021届高三模拟试题(一)北京市清华大学附属中学朝阳学校2021-2022学年高二5月月考数学试题北京市第五十七中学2021-2022学年高二下学期期末考试数学试题北京市第八中学2023届高三上学期12月测试数学试题北京市朝阳区中国人民大学朝阳分校2021-2022学年高三上学期开学考数学试题(已下线)考点47 推理与证明-备战2022年高考数学(文)一轮复习考点帮上海市上海中学2022届高三下学期高考模拟3数学试题



