2024·全国·模拟预测
解题方法
1 . 已知函数 .
.
(1)求不等式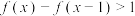 的解集;
的解集;
(2)若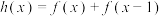 ,且存在
,且存在 使不等式
使不等式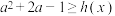 成立,求实数
成立,求实数 的取值范围.
的取值范围.
 .
.(1)求不等式
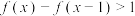 的解集;
的解集;(2)若
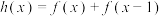 ,且存在
,且存在 使不等式
使不等式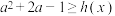 成立,求实数
成立,求实数 的取值范围.
的取值范围.
您最近半年使用:0次
2024高三·全国·专题练习
解题方法
2 . 材料1.类比是获取数学知识的重要思想之一,很多优美的数学结论就是利用类比思想获得的.例如:若 ,
, ,则
,则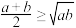 ,当且仅当
,当且仅当 时,取等号,我们称为二元均值不等式.类比二元均值不等式得到三元均值不等式:
时,取等号,我们称为二元均值不等式.类比二元均值不等式得到三元均值不等式: ,
, ,
, ,则
,则 ,当且仅当
,当且仅当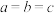 时,取等号.我们经常用它们求相关代数式或几何问题的最值,某同学做下面几何问题就是用三元均值不等式圆满完成解答的.
时,取等号.我们经常用它们求相关代数式或几何问题的最值,某同学做下面几何问题就是用三元均值不等式圆满完成解答的.
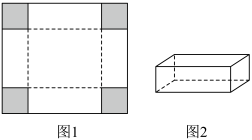
题:将边长为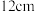 的正方形硬纸片(如图1)的四个角裁去四个相同的小正方形后,折成如图2的无盖长方体小纸盒,求纸盒容积的最大值.
的正方形硬纸片(如图1)的四个角裁去四个相同的小正方形后,折成如图2的无盖长方体小纸盒,求纸盒容积的最大值.
您最近半年使用:0次
2024高一上·全国·专题练习
3 . 一个盒子中红、白、黑三种球分别为x个、y个、z个,黑球个数至少是白球个数的一半,至多是红球个数的 ,白球与黑球的个数之和至少为55,试用不等式(组)将题中的不等关系表示出来.
,白球与黑球的个数之和至少为55,试用不等式(组)将题中的不等关系表示出来.
 ,白球与黑球的个数之和至少为55,试用不等式(组)将题中的不等关系表示出来.
,白球与黑球的个数之和至少为55,试用不等式(组)将题中的不等关系表示出来.
您最近半年使用:0次
解题方法
4 . 近日,随着新冠肺炎疫情在多地零星散发,为最大程度减少人员流动,减少疫情发生的可能性,高邮政府积极制定政策,决定政企联动,鼓励企业在国庆期间留住员工在本市过节并加班追产,为此,高邮政府决定为波司登制衣有限公司在国庆期间加班追产提供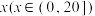 (万元)的专项补贴.波司登制衣有限公司在收到高邮政府
(万元)的专项补贴.波司登制衣有限公司在收到高邮政府 (万元)补贴后,产量将增加到
(万元)补贴后,产量将增加到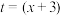 (万件).同时波司登制衣有限公司生产
(万件).同时波司登制衣有限公司生产 (万件)产品需要投入成本为
(万件)产品需要投入成本为 (万元),并以每件
(万元),并以每件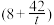 元的价格将其生产的产品全部售出.注:收益=销售金额
元的价格将其生产的产品全部售出.注:收益=销售金额 政府专项补贴
政府专项补贴 成本.
成本.
(1)求波司登制衣有限公司国庆期间,加班追产所获收益 (万元)关于政府补贴
(万元)关于政府补贴 (万元)的表达式;
(万元)的表达式;
(2)高邮政府的专项补贴为多少万元时,波司登制衣有限公司国庆期间加班追产所获收益 (万元)最大?
(万元)最大?
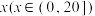 (万元)的专项补贴.波司登制衣有限公司在收到高邮政府
(万元)的专项补贴.波司登制衣有限公司在收到高邮政府 (万元)补贴后,产量将增加到
(万元)补贴后,产量将增加到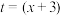 (万件).同时波司登制衣有限公司生产
(万件).同时波司登制衣有限公司生产 (万件)产品需要投入成本为
(万件)产品需要投入成本为 (万元),并以每件
(万元),并以每件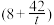 元的价格将其生产的产品全部售出.注:收益=销售金额
元的价格将其生产的产品全部售出.注:收益=销售金额 政府专项补贴
政府专项补贴 成本.
成本.(1)求波司登制衣有限公司国庆期间,加班追产所获收益
 (万元)关于政府补贴
(万元)关于政府补贴 (万元)的表达式;
(万元)的表达式;(2)高邮政府的专项补贴为多少万元时,波司登制衣有限公司国庆期间加班追产所获收益
 (万元)最大?
(万元)最大?
您最近半年使用:0次
2023-06-08更新
|
1719次组卷
|
9卷引用:江苏省扬州市高邮市2022-2023学年高一上学期10月阶段测试数学试题
江苏省扬州市高邮市2022-2023学年高一上学期10月阶段测试数学试题(已下线)第07讲 基本不等式-【暑假自学课】(人教A版2019必修第一册)(已下线)第3课时 课后 基本不等式的应用(完成)(已下线)2.2 基本不等式(精讲)-《一隅三反》(已下线)3.2 基本不等式(6大题型)-【题型分类归纳】(苏教版2019必修第一册)(已下线)第二章 等式与不等式(单元测试)(能力卷)-高一数学同步精品课堂(人教B版2019必修第一册)(已下线)考点巩固卷02 一元二次不等式及基本不等式(十二大考点)(已下线)专题02 一元二次函数、方程和不等式2-2024年高一数学寒假作业单元合订本【名校面对面】2023-2024学年高一上学期第一次月考数学试题
5 . 某公司一年购买某种货物400吨,每次都购买 吨(
吨( ),运费为4万元/次,一年的总存储费用为
),运费为4万元/次,一年的总存储费用为 万元,用
万元,用 表示一年的总运费与总存储费用之和.
表示一年的总运费与总存储费用之和.
(1)请用 的表达式表示出
的表达式表示出 ;
;
(2)要使一年的总运费与总存储费用之和最小,则每次购买多少吨;
(3)要使一年的总运费与总存储费用之和不超过200万元,则每次购买量需要在什么范围内?
 吨(
吨( ),运费为4万元/次,一年的总存储费用为
),运费为4万元/次,一年的总存储费用为 万元,用
万元,用 表示一年的总运费与总存储费用之和.
表示一年的总运费与总存储费用之和.(1)请用
 的表达式表示出
的表达式表示出 ;
;(2)要使一年的总运费与总存储费用之和最小,则每次购买多少吨;
(3)要使一年的总运费与总存储费用之和不超过200万元,则每次购买量需要在什么范围内?
您最近半年使用:0次
2021-11-05更新
|
320次组卷
|
3卷引用:上海市浦东新区2021-2022学年高一上学期期中数学试题
解题方法
6 . 新能源汽车环保、节能,以电代油,代表了世界汽车产业发展的方向.某新能源公司年初购入一批新能源汽车充电桩,每台12800元,第一年每台充电桩的维修保养费用为1000元,以后每年增加400元,每台充电桩每年可给公司带来6400元的收益.
(1)每台充电桩都从第几年开始获利?(参考数据: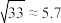 )
)
(2)每台充电桩第几年的年平均利润最大?(前n年的年平均利润 )
)
(1)每台充电桩都从第几年开始获利?(参考数据:
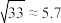 )
)(2)每台充电桩第几年的年平均利润最大?(前n年的年平均利润
 )
)
您最近半年使用:0次
名校
解题方法
7 . 某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本 万元与年产量
万元与年产量 吨之间的函数关系可以近似地表示为
吨之间的函数关系可以近似地表示为 ,已知此生产线的年产量最小为60吨,最大为110吨.
,已知此生产线的年产量最小为60吨,最大为110吨.
(1)年产量为多少吨时,生产每吨产品的平均成本最低?并求最低平均成本;
(2)若每吨产品的平均出厂价为24万元,且产品能全部售出,则年产量为多少吨时,可以获得最大利润?并求最大利润.
 万元与年产量
万元与年产量 吨之间的函数关系可以近似地表示为
吨之间的函数关系可以近似地表示为 ,已知此生产线的年产量最小为60吨,最大为110吨.
,已知此生产线的年产量最小为60吨,最大为110吨.(1)年产量为多少吨时,生产每吨产品的平均成本最低?并求最低平均成本;
(2)若每吨产品的平均出厂价为24万元,且产品能全部售出,则年产量为多少吨时,可以获得最大利润?并求最大利润.
您最近半年使用:0次
2021-07-08更新
|
4962次组卷
|
27卷引用:2021年江苏省普通高考对口单招文化统考数学试题
2021年江苏省普通高考对口单招文化统考数学试题(已下线)第32讲 基本不等式 (讲)- 2022年高考数学一轮复习讲练测(课标全国版)(已下线)专题二 能力提升检测卷(测)- 2022年高考数学一轮复习讲练测(课标全国版)(已下线)课时10 基本不等式及其应用-2022年高考数学一轮复习小题多维练(上海专用)(已下线)专题10 不等式、推理与证明、算法初步、复数-2021年高考真题和模拟题数学(文)分项汇编(全国通用)(已下线)考向08 函数的应用-备战2022年高考数学一轮复习考点微专题(上海专用)炎德英才联考合作体2021-2022学年高三上学期10月联考数学试题湖南省长沙市长郡中学2021-2022学年高三上学期10月月考数学试题广东省南海区佛山市超盈实验中学、佛山市美术实验中学2021-2022学年高一上学期第一次学科素养监测(月考)数学试题(已下线)专题10 不等式、算法初步、复数-五年(2017-2021)高考数学真题分项汇编(文科+理科)湖南省名校联合体2021-2022学年高三上学期10月联考数学试题(已下线)专题01 函数性质、方程、不等式等相结合问题(讲)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》(已下线)专题01 函数性质、方程、不等式等相结合问题(讲)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(浙江专用)》(已下线)专题10 函数应用问题-学会解题之高三数学万能解题模板【2022版】(已下线)专题13 《不等式》中的高考真题训练-2021-2022学年高一数学上册同步培优训练系列(苏教版2019)(已下线)第03讲 基本不等式(讲+练)-2023年高考数学一轮复习讲练测(新教材新高考)(已下线)考向09 幂函数与二次函数(重点)(已下线)第09讲 函数模型及其应用(精讲+精练)-2重庆市杨家坪中学2022-2023学年高一上学期10月月考数学试题(已下线)第03讲 基本不等式 (精讲+精练)-2广东省东莞市第一中学2022-2023学年高一上学期第一次月考数学试题四川省成都市石室中学2022-2023学年高一上学期第二次质量检测数学理科试题河南省洛阳市第一中学2022-2023学年高一上学期12月月考数学试题贵州省松桃苗族自治县群希高级中学有限公司2022-2023学年高一上学期第一次月考数学试题山东省菏泽市单县2022-2023学年高一上学期期末数学试题(已下线)2.2.4 均值不等式及其应用(第2课时)(分层练习)-高一数学同步精品课堂(人教B版2019必修第一册)重庆市辅仁中学校2023-2024学年高一上学期期中考试数学试题
名校
8 . 某建筑公司用8 000万元购得一块空地,计划在该地块上建造一栋至少12层、每层4 000平方米的楼房.经初步估计得知,如果将楼房建为x(x≥12)层,则每平方米的平均建筑费用为Q(x)=3 000+50x(单位:元).
(1)求楼房每平方米的平均综合费用f(x)的解析式.
(2)为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?每平方米的平均综合费用最小值是多少?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=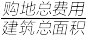 )
)
(1)求楼房每平方米的平均综合费用f(x)的解析式.
(2)为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?每平方米的平均综合费用最小值是多少?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=
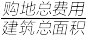 )
)
您最近半年使用:0次
2017-09-02更新
|
470次组卷
|
4卷引用:山东省寿光现代中学2018届高三上学期开学考试数学(文)试题



