名校
解题方法
1 . 已知函数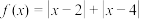 .
.
(1)求不等式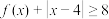 的解集;
的解集;
(2)若 的最小值为m,
的最小值为m,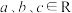 ,且满足
,且满足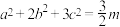 ,证明:
,证明: .
.
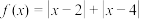 .
.(1)求不等式
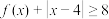 的解集;
的解集;(2)若
 的最小值为m,
的最小值为m,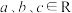 ,且满足
,且满足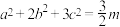 ,证明:
,证明: .
.
您最近一年使用:0次
2023-03-10更新
|
101次组卷
|
4卷引用:陕西省榆林市神木中学2020-2021学年高三下学期第一次月考文科数学试题
名校
2 . 已知函数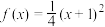 .
.
(1)证明: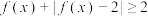 .
.
(2)若存在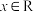 且
且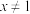 ,使得
,使得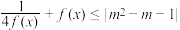 成立,求m的取值范围.
成立,求m的取值范围.
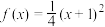 .
.(1)证明:
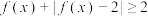 .
.(2)若存在
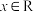 且
且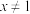 ,使得
,使得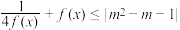 成立,求m的取值范围.
成立,求m的取值范围.
您最近一年使用:0次
名校
解题方法
3 . 已知函数 .
.
(1)求不等式 的解集
的解集 ;
;
(2)设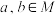 ,证明:
,证明: .
.
 .
.(1)求不等式
 的解集
的解集 ;
;(2)设
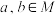 ,证明:
,证明: .
.
您最近一年使用:0次
解题方法
4 . (1)当 时,求证:
时,求证: ;
;
(2)已知 a,b,c是互不相等的正实数,求证: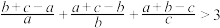 .
.
 时,求证:
时,求证: ;
;(2)已知 a,b,c是互不相等的正实数,求证:
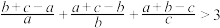 .
.
您最近一年使用:0次
2021-09-08更新
|
90次组卷
|
2卷引用:陕西省渭南市尚德中学2020-2021学年高二下学期第二次质量检测文科数学试题
名校
解题方法
5 . 已知函数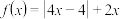 .
.
(1)求不等式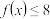 的解集;
的解集;
(2)证明: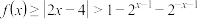 .
.
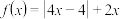 .
.(1)求不等式
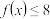 的解集;
的解集;(2)证明:
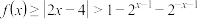 .
.
您最近一年使用:0次
名校
6 . 已知函数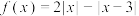 .
.
(1)求函数 的最小值;
的最小值;
(2)记函数 的最小值为
的最小值为 ,若实数
,若实数 ,
, ,
, 满足
满足 .证明
.证明 .
.
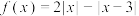 .
.(1)求函数
 的最小值;
的最小值;(2)记函数
 的最小值为
的最小值为 ,若实数
,若实数 ,
, ,
, 满足
满足 .证明
.证明 .
.
您最近一年使用:0次
2021-11-09更新
|
399次组卷
|
4卷引用:陕西省西安中学2021-2022学年高三上学期12月第三次月考文科数学试题
解题方法
7 . 已知函数 且
且 为非零常数.
为非零常数.
(1)当 时,求
时,求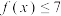 的解集;
的解集;
(2)当 时,求证
时,求证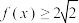 .
.
 且
且 为非零常数.
为非零常数.(1)当
 时,求
时,求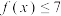 的解集;
的解集;(2)当
 时,求证
时,求证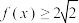 .
.
您最近一年使用:0次
名校
8 . 已知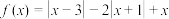 .
.
(Ⅰ)解不等式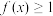 ;
;
(Ⅱ)求证: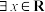 ,对
,对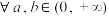 ,
,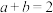 ,不等式
,不等式 成立.
成立.
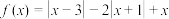 .
.(Ⅰ)解不等式
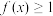 ;
;(Ⅱ)求证:
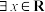 ,对
,对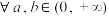 ,
,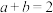 ,不等式
,不等式 成立.
成立.
您最近一年使用:0次
2021-03-13更新
|
493次组卷
|
4卷引用:陕西省西安市八校2021届高三下学期第二次联考文科数学试题
陕西省西安市八校2021届高三下学期第二次联考文科数学试题陕西省西安市八校2021届高三下学期第二次联考理科数学试题(已下线)必刷卷05-2021年高考数学(理)考前信息必刷卷(新课标卷)黑龙江省哈尔滨市第六中学2021届高三二模数学(文科)试题
名校
解题方法
9 . 已知函数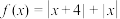 .
.
(1)解不等式 ;
;
(2)记函数 的最小值为
的最小值为 ,且
,且 ,其中
,其中 均为正实数,求证:
均为正实数,求证:
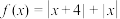 .
.(1)解不等式
 ;
;(2)记函数
 的最小值为
的最小值为 ,且
,且 ,其中
,其中 均为正实数,求证:
均为正实数,求证:
您最近一年使用:0次
2021-05-07更新
|
888次组卷
|
10卷引用:陕西省西安中学2021届高三下学期第六次模拟理科数学试题
陕西省西安中学2021届高三下学期第六次模拟理科数学试题贵州省铜仁市思南中学2021届高三第十二次考试数学(理)试题贵州省铜仁市思南中学2021届高三第十二次考试数学(文)试题安徽省马鞍山市2021届高三下学期第二次教学质量监测文科数学试题(已下线)押第23题 不等式选讲-备战2021年高考数学(文)临考题号押题(全国卷1)(已下线)押第23题 不等式选讲-备战2021年高考数学(理)临考题号押题(全国卷1)安徽省马鞍山市2021届高三下学期第二次教学质量监测理科数学试题(已下线)2021年全国高考甲卷数学(理)试题变式题21-23题(已下线)2021年全国高考甲卷数学(理)试题变式题21-23题(已下线)专题28 证明不等式的常见技巧-学会解题之高三数学万能解题模板【2022版】
名校
解题方法
10 . 已知函数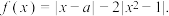
(1)当 时,
时,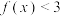 ,求实数
,求实数 的取值范围;
的取值范围;
(2)若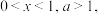 求证:
求证: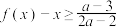 .
.
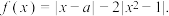
(1)当
 时,
时,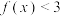 ,求实数
,求实数 的取值范围;
的取值范围;(2)若
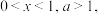 求证:
求证: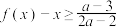 .
.
您最近一年使用:0次
2021-05-01更新
|
473次组卷
|
3卷引用:陕西省西安中学2021届高三下学期第六次模拟数学(文)试题



