1 . 已知数列 满足
满足 则
则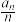 的最小值为__________.
的最小值为__________.
 满足
满足 则
则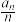 的最小值为__________.
的最小值为__________.
您最近一年使用:0次
2019-01-30更新
|
4285次组卷
|
51卷引用:2011-2012学年江苏省重点中学高二上学期开学检测数学
(已下线)2011-2012学年江苏省重点中学高二上学期开学检测数学安徽省六安市舒城中学2020-2021学年高二上学期开学考试数学(文)试题(已下线)2010年辽宁省抚顺一中高二上学期10月月考数学卷(已下线)2011-2012学年福建省龙岩一中上学期高二期中文科数学试卷2016-2017学年河南省平顶山市高二上学期期末调研考试数学(文)试卷河北省衡水中学2016-2017学年高二下学期期末考试数学(理)试题广东省深圳市耀华实验学校2017-2018学年高二(实验班)上学期期中考试数学(理)试题(已下线)模块综合检测(B)-2018-2019版数学创新设计课堂讲义同步系列(苏教版必修5)沪教版 高二年级第一学期 领航者 第七章7.9 复习与小结(1)天津市和平区耀华中学2019-2020学年高二上学期期中数学试题河南省周口市扶沟县包屯高级中学2019-2020学年高二上学期期末数学试题(已下线)河南省平顶山市2016-2017学年高二上学期期末调研考试文数试题人教A版(2019) 选择性必修第二册 过关斩将 第四章 数列 专题强化练3 数列的递推公式及通项公式上海市七宝中学2024-2025学年高二上学期开学考试数学试卷2010年普通高等学校招生全国统一考试(辽宁卷)理科数学(已下线)2011届安徽师大附中高三第一次模拟考试文科数学卷(已下线)2011届黑龙江省哈尔滨市第六中学高三上学期期中考试理科数学卷(已下线)2011-2012学年吉林省长春市十一高中高一下学期期中理科数学试卷2015届天津市南开中学高三第二次月考理科数学试卷2014-2015学年江苏省扬中市第二高级中学高一下学期周练习数学试卷2014-2015学年湖北省黄冈市高一下学期期末考试数学试卷2016届宁夏六盘山高级中学高三第一次模拟考试理科数学试卷2016届吉林大学附中高三第二次模拟理科数学试卷河北省大名县第一中学2018届高三(实验班)上学期第一次月考数学(文)试题内蒙古包头市第三十三中2016-2017学年高一下学期期末考试理数试卷河北省承德市实验中学2018届高三上学期期中考试数学(理)试题(已下线)二轮复习 【理】专题23 填空题解题方法 押题专练(已下线)二轮复习【文】专题21 填空题解题方法 押题专练辽宁省普兰店市第一中学2019届高三上学期期中考试数学(理)试题辽宁省普兰店市第一中学2019届高三上学期期中考试数学(文)试题新疆奎屯市第一高级中学2018-2019学年高一下学期第一次月考数学(理)试题河北省石家庄二中2019-2020学年高三年级上学期12月月考理科数学试卷黑龙江省哈尔滨市第三中学2018-2019学年高一下学期期末数学试题2020届海南省海南中学高三第二次月考数学试题天津市耀华中学2020-2021学年高二上学期期末数学试题江苏省镇江中学2020-2021学年高二上学期期末数学试题上海市进才中学2021-2022学年高二上学期9月月考数学试题陕西省延安市宝塔四中2021-2022学年高二上学期第一次质检数学试题安徽省亳州市第一中学2021-2022学年高二下学期3月月考数学试题沪教版(2020) 选修第一册 领航者 第4章 复习与小结(1)沪教版(2020) 选修第一册 同步跟踪练习 第4章 测试卷沪教版(2020) 选修第一册 精准辅导 第4章 4.3(2)利用递推公式表示数列上海市洋泾中学2022-2023学年高二上学期10月质量检测数学试题上海市华东师范大学第三附属中学2021-2022学年高二下学期3月月考数学试题上海市吴淞中学2022-2023学年高二上学期期末数学试题云南省曲靖一中麒麟学校2021-2022学年高二上学期期末摸底考试数学试题天津市和平区耀华中学2023-2024学年高二上学期12月月考数学试题【基础卷】第四章数列复习与小结(1)单元测试A-沪教版(2020)选择性必修第一册(已下线)专题2 数列的最大项与最小项 微点3 判断数列的最大(小)项之导数法北京名校2023届高三一轮总复习 第5章 数列 5.1 数列的有关概念(已下线)第01讲 数列的基本知识与概念(六大题型)(练习)
名校
解题方法
2 . 若数列 的通项公式分别是
的通项公式分别是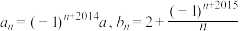 ,且
,且 对任意
对任意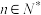 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( )
 的通项公式分别是
的通项公式分别是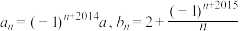 ,且
,且 对任意
对任意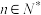 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( )A.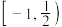 | B. | C. | D. |
您最近一年使用:0次
2019-01-30更新
|
835次组卷
|
3卷引用:山西省晋城市第一中学校2022-2023学年高二下学期开学考试数学试题
名校
3 . 已知 的定义域为
的定义域为 ,数列
,数列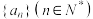 满足
满足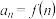 ,且
,且 是递增数列,则
是递增数列,则 的取值范围是
的取值范围是
 的定义域为
的定义域为 ,数列
,数列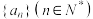 满足
满足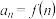 ,且
,且 是递增数列,则
是递增数列,则 的取值范围是
的取值范围是A. | B. | C.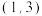 | D. |
您最近一年使用:0次
2018-03-29更新
|
952次组卷
|
4卷引用:海南省海口市第四中学2019-2020学年高二下学期开学考试数学试题
名校
解题方法
4 . 已知数列 满足:
满足: ,
, .
.
( )求
)求 ,
, ,
, 的值.
的值.
( )求证:数列
)求证:数列 是等比数列.
是等比数列.
( )令
)令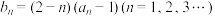 ,如果对任意
,如果对任意 ,都有
,都有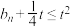 ,求实数
,求实数 的取值范围.
的取值范围.
 满足:
满足: ,
, .
.(
 )求
)求 ,
, ,
, 的值.
的值.(
 )求证:数列
)求证:数列 是等比数列.
是等比数列.(
 )令
)令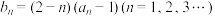 ,如果对任意
,如果对任意 ,都有
,都有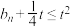 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2018-04-02更新
|
725次组卷
|
6卷引用:吉林省长春实验中学2020-2021学年高二上学期开学考试数学试题
2013·陕西西安·模拟预测
名校
5 . 已知函数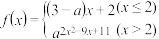 ,(
,( ,且
,且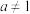 ),若数列
),若数列 满足
满足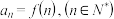 ,且
,且 是递增数列,则实数
是递增数列,则实数 的取值范围是
的取值范围是
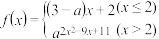 ,(
,( ,且
,且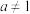 ),若数列
),若数列 满足
满足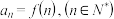 ,且
,且 是递增数列,则实数
是递增数列,则实数 的取值范围是
的取值范围是A.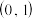 | B.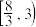 | C.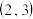 | D.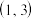 |
您最近一年使用:0次
2018-12-16更新
|
1273次组卷
|
4卷引用:【校级联考】福建省闽侯二中五校教学联合体2017-2018学年高二上学期期中考试数学(理)试题
【校级联考】福建省闽侯二中五校教学联合体2017-2018学年高二上学期期中考试数学(理)试题吉林省长春实验中学2020-2021学年高二上学期开学考试数学试题(已下线)2013届陕西省西安市西北工业大学附中高三第十二次适应性训练理数学卷智能测评与辅导[理]-数列的综合应用
名校
解题方法
6 . 设 是等比数列,公比
是等比数列,公比 ,
, 为
为 的前
的前 项和,记
项和,记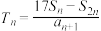 ,
,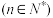 ,设
,设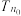 为数列
为数列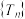 的最大项,则
的最大项,则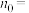
 是等比数列,公比
是等比数列,公比 ,
, 为
为 的前
的前 项和,记
项和,记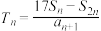 ,
,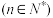 ,设
,设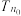 为数列
为数列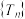 的最大项,则
的最大项,则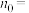
| A.2 | B.3 | C.4 | D.5 |
您最近一年使用:0次
7 . 已知数列 的前
的前 项和为
项和为 ,且满足
,且满足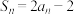 ;数列
;数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,
, ,
, .
.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)是否存在正整数 ,使得
,使得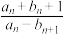 恰为数列
恰为数列 中的一项?若存在,求所有满足要求的
中的一项?若存在,求所有满足要求的 ;若不存在,说明理由.
;若不存在,说明理由.
 的前
的前 项和为
项和为 ,且满足
,且满足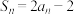 ;数列
;数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,
, ,
, .
.(1)求数列
 、
、 的通项公式;
的通项公式;(2)是否存在正整数
 ,使得
,使得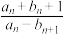 恰为数列
恰为数列 中的一项?若存在,求所有满足要求的
中的一项?若存在,求所有满足要求的 ;若不存在,说明理由.
;若不存在,说明理由.
您最近一年使用:0次
2017-09-07更新
|
1106次组卷
|
5卷引用:江苏省泰州中学2017-2018学年度高二上学期开学摸底考试数学试题
江苏省泰州中学2017-2018学年度高二上学期开学摸底考试数学试题江苏省泰州中学2017-2018学年高二上学期期初学情检测(小高考模拟)数学试题(已下线)《2018届优等生百日闯关系列》【江苏版】专题二 第六关 以新定义数列为背景的解答题2020届江苏省南通市如东县栟茶中学高三下学期5月模拟数学试题湖北省部分名校2023届高三二模数学试题
名校
8 . 设 为数列
为数列 的前
的前 项和, 已知
项和, 已知 , 对任意
, 对任意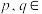 N
N , 都有
, 都有 , 则
, 则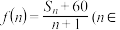 N
N )的最小值为
)的最小值为__________ .
 为数列
为数列 的前
的前 项和, 已知
项和, 已知 , 对任意
, 对任意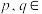 N
N , 都有
, 都有 , 则
, 则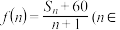 N
N )的最小值为
)的最小值为
您最近一年使用:0次
2017-03-17更新
|
2799次组卷
|
10卷引用:河北省邯郸市第二中学2017-2018学年高二上学期期中考试数学试题
河北省邯郸市第二中学2017-2018学年高二上学期期中考试数学试题【全国百强校】吉林省长春市实验中学2019届高三上学期开学考试数学(理)试题【全国百强校】云南省玉溪第一中学2018-2019学年高二上学期第二次月考数学(理)试题四川省雅安市天立教育集团2023-2024学年高二下学期开学考试数学试题2017届广东省广州市高三3月综合测试(一)数学理试卷四川省成都市9校2017届高三第四次联合模拟文科数学试题四川省成都市9校2017届高三第四次联合模拟理科数学试题江西省宜春昌黎实验学校2018届高三第二次段考数学(理科)试题(已下线)广东省广州市2017届高三下学期第一次模拟考试数学(理)试题(已下线)考点36 等差数列-备战2021年高考数学经典小题考前必刷(新高考地区专用)
解题方法
9 . 设不等式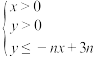 所表示的平面区域为
所表示的平面区域为 ,记
,记 内的整点个数为
内的整点个数为 (n∈
(n∈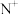 ),(整点即横坐标和纵坐标均为整数的点).
),(整点即横坐标和纵坐标均为整数的点).
(1)求数列{an}的通项公式;
(2)记数列{an}的前项和为Sn,且 ,若对于一切正整数n,总有
,若对于一切正整数n,总有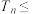 m,求实数m的取值范围.
m,求实数m的取值范围.
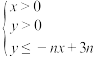 所表示的平面区域为
所表示的平面区域为 ,记
,记 内的整点个数为
内的整点个数为 (n∈
(n∈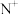 ),(整点即横坐标和纵坐标均为整数的点).
),(整点即横坐标和纵坐标均为整数的点).(1)求数列{an}的通项公式;
(2)记数列{an}的前项和为Sn,且
 ,若对于一切正整数n,总有
,若对于一切正整数n,总有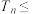 m,求实数m的取值范围.
m,求实数m的取值范围.
您最近一年使用:0次
名校
10 . 已知 ,那么数列
,那么数列 是
是
 ,那么数列
,那么数列 是
是| A.递减数列 | B.递增数列 |
| C.常数列 | D.摆动数列 |
您最近一年使用:0次
2016-12-04更新
|
561次组卷
|
7卷引用:2016-2017学年安徽六安一中高二上文周末检测三数学试卷
2016-2017学年安徽六安一中高二上文周末检测三数学试卷福建省宁德第一中学2021-2022学年高二上学期开学考试数学试题2017届河北武邑中学高三周考10.9数学(理)试卷山西省朔州市怀仁一中2018-2019学年高一下学期第四次月考数学(文)试题江西省南昌市第八中学2018-2019学年高一下学期3月月考数学试题(已下线)第26讲 数列的概念与简单表示(讲)- 2022年高考数学一轮复习讲练测(课标全国版)(已下线)6.1 数列的概念与简单表示方法课前·考点引领基础再现



