名校
1 . 在三棱锥 中,
中, 和
和 都是等边三角形,
都是等边三角形,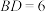 ,平面
,平面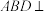 平面
平面 ,M是棱AC上一点,且
,M是棱AC上一点,且 ,则过M的平面截三棱锥
,则过M的平面截三棱锥 外接球所得截面面积的最大值与最小值之和为( )
外接球所得截面面积的最大值与最小值之和为( )
 中,
中, 和
和 都是等边三角形,
都是等边三角形,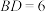 ,平面
,平面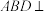 平面
平面 ,M是棱AC上一点,且
,M是棱AC上一点,且 ,则过M的平面截三棱锥
,则过M的平面截三棱锥 外接球所得截面面积的最大值与最小值之和为( )
外接球所得截面面积的最大值与最小值之和为( )| A.24π | B.25π | C.26π | D.27π |
您最近一年使用:0次
名校
2 . 如今中国被誉为基建狂魔,可谓是逢山开路,遇水架桥.公路里程、高铁里程双双都是世界第一.建设过程中研制出用于基建的大型龙门吊、平衡盾构机等国之重器更是世界领先.如图是某重器上一零件结构模型,中间最大球为正四面体 的内切球,中等球与最大球和正四面体三个面均相切,最小球与中等球和正四面体三个面均相切,已知正四面体
的内切球,中等球与最大球和正四面体三个面均相切,最小球与中等球和正四面体三个面均相切,已知正四面体 棱长为
棱长为 ,则模型中九个球的表面积和为( )
,则模型中九个球的表面积和为( )
 的内切球,中等球与最大球和正四面体三个面均相切,最小球与中等球和正四面体三个面均相切,已知正四面体
的内切球,中等球与最大球和正四面体三个面均相切,最小球与中等球和正四面体三个面均相切,已知正四面体 棱长为
棱长为 ,则模型中九个球的表面积和为( )
,则模型中九个球的表面积和为( )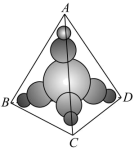
A.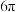 | B. | C.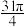 | D.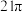 |
您最近一年使用:0次
2023-06-14更新
|
2476次组卷
|
12卷引用:湖北省武昌实验中学2023-2024学年高三上学期10月月考数学试题
湖北省武昌实验中学2023-2024学年高三上学期10月月考数学试题浙江省乐清市知临中学2023届高三下学期5月第二次仿真考数学试题湖南省长沙市雅礼中学2024届高三上学期月考(一)数学试题(已下线)重难点突破01 玩转外接球、内切球、棱切球(二十三大题型)-5浙江省杭州市北斗联盟2023-2024学年高二上学期期中联考数学试题(已下线)考点7 组合体的内切 2024届高考数学考点总动员【练】(已下线)重难点6-3 立体几何外接球与内切球问题(12题型+满分技巧+限时检测)(已下线)专题15 球体外接内切综合问题小题(已下线)专题7.1 基本立体图形、简单几何体的表面积与体积【八大题型】(已下线)重难点11 立体几何常考经典小题全归类【九大题型】天津市部分学校2023-2024学年高三下学期第一次质量调查数学试卷(已下线)【类题归纳】正四面体 基底建系
解题方法
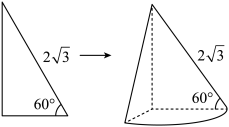
3 . 农历五月初五是端午节.这一天民间有吃粽子的习俗,据说是为了纪念战国时期楚国大臣、爱国诗人屈原.粽子的形状有多种.今有某种粽子类似于由一个直角三角形绕它的一条直角边旋转 (如图)而成.如果粽子的馅可以看成是这个几何体内的一个球状物,则粽子馅的最大体积为
(如图)而成.如果粽子的馅可以看成是这个几何体内的一个球状物,则粽子馅的最大体积为______ .
 (如图)而成.如果粽子的馅可以看成是这个几何体内的一个球状物,则粽子馅的最大体积为
(如图)而成.如果粽子的馅可以看成是这个几何体内的一个球状物,则粽子馅的最大体积为
您最近一年使用:0次
名校
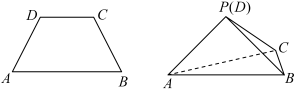
4 . 如图,在等腰梯形ABCD中,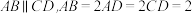 .将△ACD沿着AC翻折,使得点D到点P,且
.将△ACD沿着AC翻折,使得点D到点P,且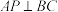 .下列结论正确的是( )
.下列结论正确的是( )
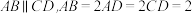 .将△ACD沿着AC翻折,使得点D到点P,且
.将△ACD沿着AC翻折,使得点D到点P,且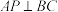 .下列结论正确的是( )
.下列结论正确的是( )
| A.平面APC⊥平面ABC |
B.二面角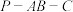 的大小为 的大小为 |
C.三棱锥 的外接球的表面积为5π 的外接球的表面积为5π |
D.点C到平面APB的距离为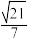 |
您最近一年使用:0次
2023-06-09更新
|
529次组卷
|
5卷引用:湖北省新高考协作体2022-2023学年高一下学期5月联考数学试题
5 . 在正方体 中,E,F分别为AB,
中,E,F分别为AB, 的中点,以EF为直径的球的球面与该正方体的棱共有
的中点,以EF为直径的球的球面与该正方体的棱共有____________ 个公共点.
 中,E,F分别为AB,
中,E,F分别为AB, 的中点,以EF为直径的球的球面与该正方体的棱共有
的中点,以EF为直径的球的球面与该正方体的棱共有
您最近一年使用:0次
2023-06-09更新
|
17438次组卷
|
20卷引用:湖北省黄石市部分学校2023-2024学年高二上学期期末联考数学试卷
湖北省黄石市部分学校2023-2024学年高二上学期期末联考数学试卷2023年高考全国甲卷数学(理)真题全国甲乙卷3年真题分类汇编《立体几何》选填题全国甲乙卷真题5年分类汇编《立体几何》选填全国甲乙卷5年真题分类汇编《立体几何》选填题专题06空间向量与立体几何(成品)(已下线)2023年高考全国甲卷数学(理)真题变式题11-15(已下线)专题10 空间向量与立体几何-1(已下线)模块一 情境7 以立体几何为背景山西省晋城市第一中学校2024届高三上学期8月月考数学试题山西省大同市第一中学校2023-2024学年高二上学期9月学情检测数学试题陕西省咸阳市武功县普集高级中学2024届高三上学期第4次月考数学(理)试题(已下线)模块7 空间几何篇 第1讲:内切与外接问题【练】专题08基本立体图形与直观图(已下线)专题05 空间向量与立体几何(解密讲义)(已下线)专题7.1 基本立体图形、简单几何体的表面积与体积【八大题型】(已下线)重难点11 立体几何常考经典小题全归类【九大题型】(已下线)【一题多变】外接于球 两心相连单元测试B卷——第八章?立体几何初步(已下线)专题15 立体几何多选、填空题(理科)
名校
解题方法
6 . 《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥 为鳖臑,
为鳖臑, 平面
平面 ,
, ,三棱锥P-ABC的四个顶点都在球
,三棱锥P-ABC的四个顶点都在球 的球面上,则球
的球面上,则球 的表面积为( )
的表面积为( )
 为鳖臑,
为鳖臑, 平面
平面 ,
, ,三棱锥P-ABC的四个顶点都在球
,三棱锥P-ABC的四个顶点都在球 的球面上,则球
的球面上,则球 的表面积为( )
的表面积为( )A. | B. | C.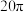 | D.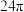 |
您最近一年使用:0次
2023-06-09更新
|
550次组卷
|
31卷引用:湖北省武汉市第四十九中2020-2021学年高一下学期5月月考数学试题
湖北省武汉市第四十九中2020-2021学年高一下学期5月月考数学试题湖北省宜昌市第一中学2021-2022学年高一下学期6月阶段性测试数学试题2017届广东省广州市高三3月综合测试(一)数学文试卷2017届广东省广州市高三3月综合测试(一)数学理试卷吉林省东北师范大学附属中学2017届高三下学期第三次模拟考试数学(文)试题河北省张家口市第一中学2016-2017学年高一(实验班、普通班)6月月考数学试题辽宁省庄河市高级中学2018届高三上学期开学考试数学(文)试题四川省成都市双流中学2017高二上学期期中考试数学试题甘肃省天水市第一中学2018届高三上学期第二次考试(期中)数学(文)试题甘肃省天水市第一中学2018届高三上学期第二学段(期中)考试数学(理)试题广东省汕头市达濠华桥中学2017-2018学年高二上学期阶段考试(二)数学理试题甘肃省天水市第一中学2018届高三上学期第二学段(期中)考试数学(文)试题(已下线)7-2 空间几何体的表面积和体积(高效训练)-2019版导学教程一轮复习数学(人教版)【全国百强校】]江西省上饶市横峰中学2019届高三考前模拟考试数学(理)试题湖南省长沙市实验中学2019-2020学年高一上学期第三次阶段性检测数学试题安徽省合肥市第十一中学2019-2020学年高二上学期期中数学(理)试题浙江省绍兴市诸暨中学2018-2019学年高二(平行班)上学期10月阶段性考试数学试题(已下线)广东省广州市2017届高三下学期第一次模拟考试数学(理)试题甘肃省武威第六中学2020-2021学年高三上学期第三次过关考试数学(文)试题(已下线)考点29 空间几何体的表面积与体积-备战2021年高考数学(理)一轮复习考点一遍过黑龙江省哈尔滨市第一中学校2020-2021学年高三上学期12月月考数学试题(已下线) 专题21几何体与球切、接的问题(讲)- 2021年高三数学二轮复习讲练测(文理通用)(已下线)专题17 几何体与球切、接的问题 (讲)-2021年高三数学二轮复习讲练测(新高考版)黑龙江省齐齐哈尔市第八中学校2020-2021学年高一下学期期中数学试题广东省揭阳市揭西县2020-2021学年高一下学期期末数学试题新疆哈密市第十五中学2020-2021学年高二下学期期末考试数学(文)试题(已下线)专题08几何体与球切、接的问题(讲)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》广西梧州市2021-2022学年高一下学期期末检测数学试题湖南省衡阳市祁东县第二中学2022-2023学年高一下学期期中数学试题(已下线)模块四 专题2 高考新题型专练(新定义专练)(人教A)(已下线)模块三 专题3 高考新题型专练(新定义专练)(北师大2019版)
名校
解题方法
7 . 在 中,
中, ,
, ,D为BC的中点,将
,D为BC的中点,将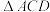 绕AD旋转至
绕AD旋转至 ,使得
,使得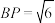 ,则三棱锥
,则三棱锥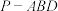 的外接球表面积为( )
的外接球表面积为( )
 中,
中, ,
, ,D为BC的中点,将
,D为BC的中点,将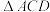 绕AD旋转至
绕AD旋转至 ,使得
,使得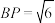 ,则三棱锥
,则三棱锥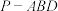 的外接球表面积为( )
的外接球表面积为( )A.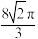 | B. | C.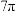 | D. |
您最近一年使用:0次
2023-06-08更新
|
337次组卷
|
3卷引用:湖北省云学新高考联盟学校2022-2023学年高一下学期5月联考数学试题
湖北省云学新高考联盟学校2022-2023学年高一下学期5月联考数学试题(已下线)6.6简单几何体的再认识-【帮课堂】(北师大版2019必修第二册)专题训练:与球有关的外接和内切问题小题精练30题-同步题型分类归纳讲与练(人教A版2019必修第二册)
名校
8 . 已知正三棱锥 的侧棱长为3,
的侧棱长为3,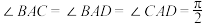 .过顶点
.过顶点 作底面
作底面 的垂线,垂足为
的垂线,垂足为 ,过点
,过点 作侧面
作侧面 的垂线,垂足为
的垂线,垂足为 ,过点
,过点 作平面
作平面 的垂线,垂足为
的垂线,垂足为 ,连接相关线段形成四面体
,连接相关线段形成四面体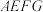 ,则四面体
,则四面体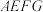 的外接球的表面积为
的外接球的表面积为______________ .
 的侧棱长为3,
的侧棱长为3,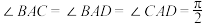 .过顶点
.过顶点 作底面
作底面 的垂线,垂足为
的垂线,垂足为 ,过点
,过点 作侧面
作侧面 的垂线,垂足为
的垂线,垂足为 ,过点
,过点 作平面
作平面 的垂线,垂足为
的垂线,垂足为 ,连接相关线段形成四面体
,连接相关线段形成四面体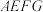 ,则四面体
,则四面体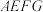 的外接球的表面积为
的外接球的表面积为
您最近一年使用:0次
2023-06-08更新
|
396次组卷
|
2卷引用:湖北省高中名校联盟2022-2023学年高一下学期5月联合测评数学试题
9 . 我国古代《九章算术》里记载了一个“羡除”的例子,羡除,隧道也,其所穿地,上平下邪,如图是一个“羡除”模型,该“羡除”是以 为顶点的五面体,四边形
为顶点的五面体,四边形 为正方形,
为正方形,
 平面
平面 ,则( )
,则( )

 为顶点的五面体,四边形
为顶点的五面体,四边形 为正方形,
为正方形,
 平面
平面 ,则( )
,则( )
A.该几何体的表面积为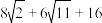 |
B.该几何体的体积为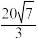 |
C.该几何体的外接球的表面积为 |
D. 与平面 与平面 所成角的正弦值为 所成角的正弦值为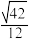 |
您最近一年使用:0次
2023-06-07更新
|
934次组卷
|
4卷引用:湖北省武汉市第二中学等校2023届高三下学期六模数学试题
湖北省武汉市第二中学等校2023届高三下学期六模数学试题广东省广州市执信中学2024届高三上学期开学测试数学试题(已下线)模块一 专题1 《立体几何》单元检测篇 B提升卷(已下线)第六章 突破立体几何创新问题 专题一 交汇中国古代文化 微点2 与中国古代文化遗产有关的立体几何问题(二)【基础版】
名校
解题方法
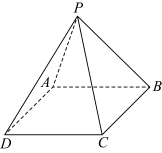
10 . 如图,已知正四棱锥 的所有棱长均为4,平面
的所有棱长均为4,平面 经过
经过 ,则平面
,则平面 截正四棱锥
截正四棱锥 的外接球所得截面圆的面积的最小值为( )
的外接球所得截面圆的面积的最小值为( )
 的所有棱长均为4,平面
的所有棱长均为4,平面 经过
经过 ,则平面
,则平面 截正四棱锥
截正四棱锥 的外接球所得截面圆的面积的最小值为( )
的外接球所得截面圆的面积的最小值为( )
A.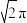 | B.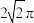 | C. | D.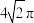 |
您最近一年使用:0次
2023-06-05更新
|
725次组卷
|
5卷引用:湖北省恩施州巴东县第三高级中学2022-2023学年高一下学期期末数学试题
湖北省恩施州巴东县第三高级中学2022-2023学年高一下学期期末数学试题安徽省江淮名校2022~2023学年高一下学期5月阶段联考数学试题江西省南昌市等5地2022-2023学年高一下学期期末联考数学试题(已下线)专题突破卷20立体几何的截面问题-1(已下线)第二章 立体几何中的计算 专题六 几何体的外接球、棱切球、内切球 微点6 正棱锥和圆锥模型综合训练【基础版】



