【课堂例】2.2.3椭圆的性质(2) 课堂例题 沪教版(2020)选择性必修第一册 第2章 圆锥曲线
上海
高二
课堂例题
2024-07-29
36次
整体难度:
容易
考查范围:
平面解析几何
一、填空题 添加题型下试题
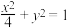 的两个焦点
的两个焦点 ,
, ,过点
,过点 作垂直于
作垂直于 轴的直线与椭圆相交,其中一个交点为
轴的直线与椭圆相交,其中一个交点为 ,则
,则
【知识点】 椭圆上点到焦点的距离及最值 求椭圆的焦点、焦距
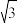 ,则这个椭圆方程为
,则这个椭圆方程为 的一个焦点为
的一个焦点为 ,M是椭圆上一点,且
,M是椭圆上一点,且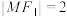 ,N是线段
,N是线段 的中点,则
的中点,则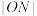 的长为
的长为【知识点】 根据椭圆方程求a、b、c 椭圆中焦点三角形的其他问题
 、
、 是椭圆
是椭圆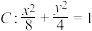 的焦点,在C上满足
的焦点,在C上满足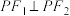 的点P的个数为
的点P的个数为【知识点】 求直线与椭圆的交点坐标
 的左、右焦点分别为
的左、右焦点分别为 ,
, ,焦距为
,焦距为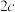 ,过点
,过点 的直线与椭圆
的直线与椭圆 交于
交于 ,
, 两点,若
两点,若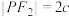 ,且
,且 ,则椭圆
,则椭圆 的离心率为
的离心率为【知识点】 求椭圆的离心率或离心率的取值范围
二、单选题 添加题型下试题
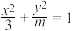 长轴的两个端点,若C上存在点M满足∠AMB=120°,则m的取值范围是
长轴的两个端点,若C上存在点M满足∠AMB=120°,则m的取值范围是A.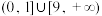 | B. |
C.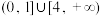 | D. |
【知识点】 求椭圆中的参数及范围
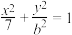 ,过原点O斜率为
,过原点O斜率为 的直线与椭圆交于C,D,若
的直线与椭圆交于C,D,若 ,则椭圆的标准方程为( )
,则椭圆的标准方程为( )A. | B.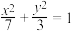 |
C.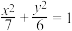 | D.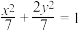 |
【知识点】 根据a、b、c求椭圆标准方程 根据弦长求参数
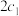 和
和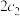 分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用
分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用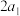 和
和 分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:
分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子: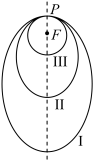
 ;②
;② ;③
;③ ;④
;④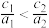 .
.其中正确式子的序号是( ).
| A.①③ | B.②③ | C.①④ | D.②④ |
【知识点】 根据椭圆方程求a、b、c
三、解答题 添加题型下试题
 、
、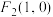 ,且椭圆C经过点
,且椭圆C经过点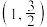 .
.(1)求椭圆C的标准方程;
(2)当m取何值时,直线
 与椭圆C:
与椭圆C:①有两个公共点;
②只有一个公共点;
③没有公共点?
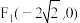 和
和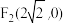 ,长轴长为6,设直线
,长轴长为6,设直线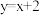 交椭圆C于A、B两点.
交椭圆C于A、B两点.求:(1)椭圆C的标准方程;
(2)弦AB的中点坐标及弦长.
【知识点】 根据a、b、c求椭圆标准方程 椭圆的中点弦 求椭圆中的弦长
11. 已知椭圆C以坐标轴为对称轴,以坐标原点为对称中心,椭圆的一个焦点为 ,点
,点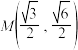 在椭圆上,
在椭圆上,
 Ⅰ
Ⅰ 求椭圆C的方程.
求椭圆C的方程.
 Ⅱ
Ⅱ 斜率为k的直线l过点F且不与坐标轴垂直,直线l交椭圆于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.
斜率为k的直线l过点F且不与坐标轴垂直,直线l交椭圆于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.
【知识点】 椭圆的中点弦
 为椭圆
为椭圆 的右顶点,点M在椭圆C的长轴上,过点M且不与x轴重合的直线交椭圆C于A,B两点,当点M与坐标原点O重合时,直线
的右顶点,点M在椭圆C的长轴上,过点M且不与x轴重合的直线交椭圆C于A,B两点,当点M与坐标原点O重合时,直线 的斜率之积为
的斜率之积为 .
.(1)求椭圆C的标准方程;
(2)若
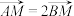 ,求
,求 面积的最大值.
面积的最大值.
【知识点】 椭圆中三角形(四边形)的面积
试卷分析
导出试卷题型(共 12题)
试卷难度
细目表分析
| 题号 | 难度系数 | 详细知识点 | 备注 |
| 一、填空题 | |||
| 1 | 0.85 | 椭圆上点到焦点的距离及最值 求椭圆的焦点、焦距 | 单空题 |
| 2 | 0.85 | 椭圆的方程与椭圆(焦点)位置的特征 根据a、b、c求椭圆标准方程 | 单空题 |
| 3 | 0.85 | 根据椭圆方程求a、b、c 椭圆中焦点三角形的其他问题 | 单空题 |
| 4 | 0.65 | 求直线与椭圆的交点坐标 | 单空题 |
| 5 | 0.65 | 求椭圆的离心率或离心率的取值范围 | 单空题 |
| 二、单选题 | |||
| 6 | 0.65 | 求椭圆中的参数及范围 | |
| 7 | 0.65 | 根据a、b、c求椭圆标准方程 根据弦长求参数 | |
| 8 | 0.65 | 根据椭圆方程求a、b、c | |
| 三、解答题 | |||
| 9 | 0.85 | 根据椭圆过的点求标准方程 根据直线与椭圆的位置关系求参数或范围 | 问答题 |
| 10 | 0.85 | 根据a、b、c求椭圆标准方程 椭圆的中点弦 求椭圆中的弦长 | 问答题 |
| 11 | 0.4 | 椭圆的中点弦 | 问答题 |
| 12 | 0.65 | 椭圆中三角形(四边形)的面积 | 问答题 |



