椭圆 的焦点
的焦点 、
、 是双曲线
是双曲线 的顶点,其顶点是双曲线
的顶点,其顶点是双曲线 的焦点.双曲线
的焦点.双曲线 的渐近线是
的渐近线是 ,椭圆
,椭圆 与双曲线
与双曲线 有一个交点
有一个交点 ,
, 的周长为
的周长为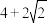 .
.
(1)求椭圆 与双曲线
与双曲线 的标准方程;
的标准方程;
(2)设直线 交双曲线
交双曲线 于
于 、
、 两点,交直线
两点,交直线 于点
于点 ,若
,若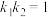 .证明:
.证明: 为
为 的中点;
的中点;
(3)过点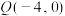 作一动直线
作一动直线 交椭圆
交椭圆 于A、
于A、 两点,记
两点,记 .若在线段
.若在线段 上取一点
上取一点 ,使得
,使得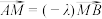 ,求点
,求点 的轨迹方程.
的轨迹方程.
 的焦点
的焦点 、
、 是双曲线
是双曲线 的顶点,其顶点是双曲线
的顶点,其顶点是双曲线 的焦点.双曲线
的焦点.双曲线 的渐近线是
的渐近线是 ,椭圆
,椭圆 与双曲线
与双曲线 有一个交点
有一个交点 ,
, 的周长为
的周长为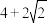 .
.(1)求椭圆
 与双曲线
与双曲线 的标准方程;
的标准方程;(2)设直线
 交双曲线
交双曲线 于
于 、
、 两点,交直线
两点,交直线 于点
于点 ,若
,若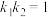 .证明:
.证明: 为
为 的中点;
的中点;(3)过点
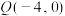 作一动直线
作一动直线 交椭圆
交椭圆 于A、
于A、 两点,记
两点,记 .若在线段
.若在线段 上取一点
上取一点 ,使得
,使得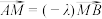 ,求点
,求点 的轨迹方程.
的轨迹方程.
更新时间:2023/05/27 22:22:38
|
相似题推荐
解答题-证明题
|
较难
(0.4)
名校
解题方法
【推荐1】已知椭圆 的左焦点为
的左焦点为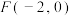 ,点
,点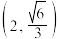 在
在 上.
上.
(1)求椭圆
 的方程;
的方程;(2)过
 的两条互相垂直的直线分别交
的两条互相垂直的直线分别交 于
于 两点和
两点和 两点,若
两点,若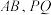 的中点分别为
的中点分别为 ,证明:直线
,证明:直线 必过定点,并求出此定点坐标.
必过定点,并求出此定点坐标.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
【推荐2】已知椭圆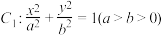 的长轴长为4,离心率为
的长轴长为4,离心率为 ,一动圆
,一动圆 过椭圆
过椭圆 右焦点
右焦点 ,且与直线
,且与直线 相切.
相切.
(1)求椭圆 的方程及动圆圆心轨迹
的方程及动圆圆心轨迹 的方程;
的方程;
(2)过 作两条互相垂直的直线,分别交椭圆
作两条互相垂直的直线,分别交椭圆 于
于 ,
, 两点,交曲线
两点,交曲线 于
于 ,
, 两点,求四边形
两点,求四边形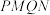 面积的最小值.
面积的最小值.
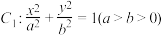 的长轴长为4,离心率为
的长轴长为4,离心率为 ,一动圆
,一动圆 过椭圆
过椭圆 右焦点
右焦点 ,且与直线
,且与直线 相切.
相切.(1)求椭圆
 的方程及动圆圆心轨迹
的方程及动圆圆心轨迹 的方程;
的方程;(2)过
 作两条互相垂直的直线,分别交椭圆
作两条互相垂直的直线,分别交椭圆 于
于 ,
, 两点,交曲线
两点,交曲线 于
于 ,
, 两点,求四边形
两点,求四边形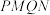 面积的最小值.
面积的最小值.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
名校
解题方法
【推荐1】以双曲线 的右焦点
的右焦点 为圆心作圆,与
为圆心作圆,与 的一条渐近线相切于点
的一条渐近线相切于点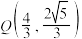
(1)求 的方程.
的方程.
(2)在 轴上是否存在定点
轴上是否存在定点 ,过点
,过点 任意作一条不与坐标轴垂直的直线
任意作一条不与坐标轴垂直的直线 ,当
,当 与
与 交于
交于 两点时,直线
两点时,直线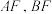 的斜率之和为定值?若存在,求出
的斜率之和为定值?若存在,求出 点的坐标,若不存在,说明理由.
点的坐标,若不存在,说明理由.
 的右焦点
的右焦点 为圆心作圆,与
为圆心作圆,与 的一条渐近线相切于点
的一条渐近线相切于点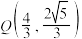
(1)求
 的方程.
的方程.(2)在
 轴上是否存在定点
轴上是否存在定点 ,过点
,过点 任意作一条不与坐标轴垂直的直线
任意作一条不与坐标轴垂直的直线 ,当
,当 与
与 交于
交于 两点时,直线
两点时,直线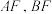 的斜率之和为定值?若存在,求出
的斜率之和为定值?若存在,求出 点的坐标,若不存在,说明理由.
点的坐标,若不存在,说明理由.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
名校
解题方法
【推荐2】已知双曲线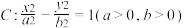 的虚轴长为4,渐近线方程为
的虚轴长为4,渐近线方程为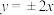 .
.
(1)求双曲线 的标准方程;
的标准方程;
(2)设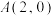 ,
, 是双曲线上的动点,求
是双曲线上的动点,求 的最小值;
的最小值;
(3)过双曲线右焦点 的直线
的直线 与双曲线
与双曲线 的左、右两支分别交于点
的左、右两支分别交于点 、
、 ,点
,点 是线段
是线段 的中点,过点
的中点,过点 且与
且与 垂直的直线
垂直的直线 交直线
交直线 于点
于点 ,点
,点 满足
满足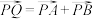 ,求四边形
,求四边形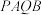 面积的最小值.
面积的最小值.
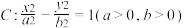 的虚轴长为4,渐近线方程为
的虚轴长为4,渐近线方程为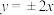 .
.(1)求双曲线
 的标准方程;
的标准方程;(2)设
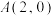 ,
, 是双曲线上的动点,求
是双曲线上的动点,求 的最小值;
的最小值;(3)过双曲线右焦点
 的直线
的直线 与双曲线
与双曲线 的左、右两支分别交于点
的左、右两支分别交于点 、
、 ,点
,点 是线段
是线段 的中点,过点
的中点,过点 且与
且与 垂直的直线
垂直的直线 交直线
交直线 于点
于点 ,点
,点 满足
满足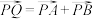 ,求四边形
,求四边形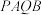 面积的最小值.
面积的最小值.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
名校
解题方法
【推荐1】设椭圆 的方程为
的方程为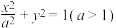 ,点
,点 为坐标原点,点
为坐标原点,点 、
、 的坐标分别为
的坐标分别为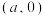 、
、 ,点
,点 在线段
在线段 上,满足
上,满足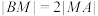 ,直线
,直线 的斜率为
的斜率为 .
.
(1)求椭圆 的方程;
的方程;
(2)若动直线 与椭圆
与椭圆 交于
交于 、
、 两点,且恒有
两点,且恒有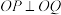 ,是否存在一个以原点
,是否存在一个以原点 为圆心的定圆
为圆心的定圆 ,使得动直线
,使得动直线 始终与定圆
始终与定圆 相切?若存在,求圆
相切?若存在,求圆 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
 的方程为
的方程为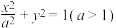 ,点
,点 为坐标原点,点
为坐标原点,点 、
、 的坐标分别为
的坐标分别为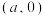 、
、 ,点
,点 在线段
在线段 上,满足
上,满足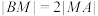 ,直线
,直线 的斜率为
的斜率为 .
.(1)求椭圆
 的方程;
的方程;(2)若动直线
 与椭圆
与椭圆 交于
交于 、
、 两点,且恒有
两点,且恒有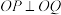 ,是否存在一个以原点
,是否存在一个以原点 为圆心的定圆
为圆心的定圆 ,使得动直线
,使得动直线 始终与定圆
始终与定圆 相切?若存在,求圆
相切?若存在,求圆 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
您最近一年使用:0次
【推荐2】已知椭圆 的离心率为e,且过
的离心率为e,且过 ,
,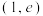 两点.
两点.
(1)求椭圆E的方程;
(2)若经过 有两条直线
有两条直线 ,
, ,它们的斜率互为倒数,
,它们的斜率互为倒数, 与椭圆E交于A,B两点,
与椭圆E交于A,B两点, 与椭圆E交于C,D两点,P,Q分别是
与椭圆E交于C,D两点,P,Q分别是 ,
, 的中点.试探究:
的中点.试探究: 与
与 的面积之比是否为定值?若是,请求出此定值;若不是,请说明理由.
的面积之比是否为定值?若是,请求出此定值;若不是,请说明理由.
 的离心率为e,且过
的离心率为e,且过 ,
,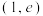 两点.
两点.(1)求椭圆E的方程;
(2)若经过
 有两条直线
有两条直线 ,
, ,它们的斜率互为倒数,
,它们的斜率互为倒数, 与椭圆E交于A,B两点,
与椭圆E交于A,B两点, 与椭圆E交于C,D两点,P,Q分别是
与椭圆E交于C,D两点,P,Q分别是 ,
, 的中点.试探究:
的中点.试探究: 与
与 的面积之比是否为定值?若是,请求出此定值;若不是,请说明理由.
的面积之比是否为定值?若是,请求出此定值;若不是,请说明理由.
您最近一年使用:0次
解答题-证明题
|
较难
(0.4)
解题方法
【推荐1】设双曲线 的焦距为6,点
的焦距为6,点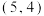 在双曲线
在双曲线 上.
上.
(1)求双曲线 的方程;
的方程;
(2)已知 的右焦点为
的右焦点为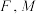 是直线
是直线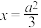 上一点,直线
上一点,直线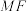 交双曲线
交双曲线 于
于 两点(
两点( 在第一象限),过点
在第一象限),过点 作直线
作直线 的平行线
的平行线 与直线
与直线 交于点
交于点 ,与
,与 轴交于点
轴交于点 ,证明:
,证明: 为线段
为线段 的中点.
的中点.
 的焦距为6,点
的焦距为6,点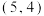 在双曲线
在双曲线 上.
上.(1)求双曲线
 的方程;
的方程;(2)已知
 的右焦点为
的右焦点为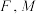 是直线
是直线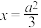 上一点,直线
上一点,直线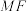 交双曲线
交双曲线 于
于 两点(
两点( 在第一象限),过点
在第一象限),过点 作直线
作直线 的平行线
的平行线 与直线
与直线 交于点
交于点 ,与
,与 轴交于点
轴交于点 ,证明:
,证明: 为线段
为线段 的中点.
的中点.
您最近一年使用:0次
【推荐2】圆锥曲线的弦与过弦的端点的两条切线所围成的三角形叫做阿基米德三角形. 在一次以“圆锥曲线的阿基米德三角形”为主题的数学探究活动中,甲同学以如图示的抛物线C: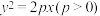 的阿基米德三角形
的阿基米德三角形 为例,经探究发现:若AB为过焦点的弦,则:①点P在定直线上;②
为例,经探究发现:若AB为过焦点的弦,则:①点P在定直线上;②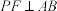 ;③
;③ .已知△PAB为等轴双曲线
.已知△PAB为等轴双曲线 的阿基米德三角形,AB过Γ的右焦点F.
的阿基米德三角形,AB过Γ的右焦点F.
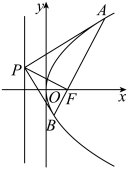
(1)试探究甲同学得出的结论,类比到此双曲线情境中,是否仍然成立?(选择一个结论进行探究即可)
(2)若 ,弦AB的中点为Q,
,弦AB的中点为Q, ,求点P的坐标.
,求点P的坐标.
(注:双曲线 的以
的以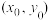 为切点的切线方程为
为切点的切线方程为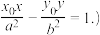
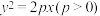 的阿基米德三角形
的阿基米德三角形 为例,经探究发现:若AB为过焦点的弦,则:①点P在定直线上;②
为例,经探究发现:若AB为过焦点的弦,则:①点P在定直线上;②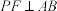 ;③
;③ .已知△PAB为等轴双曲线
.已知△PAB为等轴双曲线 的阿基米德三角形,AB过Γ的右焦点F.
的阿基米德三角形,AB过Γ的右焦点F.
(1)试探究甲同学得出的结论,类比到此双曲线情境中,是否仍然成立?(选择一个结论进行探究即可)
(2)若
 ,弦AB的中点为Q,
,弦AB的中点为Q, ,求点P的坐标.
,求点P的坐标.(注:双曲线
 的以
的以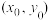 为切点的切线方程为
为切点的切线方程为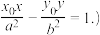
您最近一年使用:0次

 ,椭圆过点
,椭圆过点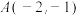 .
.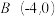 的直线
的直线 于点P,Q,求
于点P,Q,求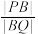 的值.
的值.
 ?若存在,求出点
?若存在,求出点 的两条切线
的两条切线 ,若切线
,若切线 ,证明:
,证明: 三点共线.
三点共线.
 (
( )中,其所有外切矩形的顶点在一个定圆
)中,其所有外切矩形的顶点在一个定圆 :
: 上,称此圆为椭圆的蒙日圆.椭圆
上,称此圆为椭圆的蒙日圆.椭圆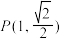 ,
, .
. ,
, 存在,证明:
存在,证明: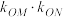 为定值.
为定值.
 的左、右焦点分别为
的左、右焦点分别为 ,过
,过 .过
.过 两点,且
两点,且 的最小值为
的最小值为 .
.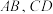 的中点分别为
的中点分别为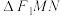 的面积为
的面积为 ,
, 的面积为
的面积为 (
( 的斜率分别为
的斜率分别为 且
且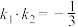 ,求证:
,求证: 为定值,并求出这个定值.
为定值,并求出这个定值.


