名校
1 . 已知在 中,点D,E分别为射线
中,点D,E分别为射线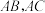 上的动点,
上的动点,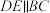 .
. 中点,点E为
中点,点E为 中点时,不借助相似证明中位线性质,求证:
中点时,不借助相似证明中位线性质,求证: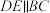 且
且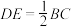 ;
;
②若 面积为25,
面积为25, 变成为10,将
变成为10,将 沿
沿 翻折,设点A落在四边形
翻折,设点A落在四边形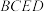 内部的点Q处,设
内部的点Q处,设 为x,
为x,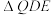 的面积为y,求:y关于x的函数解析式及其定义域;
的面积为y,求:y关于x的函数解析式及其定义域;
(2)若当点D,E在边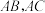 上时,且
上时,且 ,
, 和
和 的重心距为2,当点D,E分别在
的重心距为2,当点D,E分别在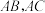 延长线上时,
延长线上时, 与
与 重心距不大于6,求:
重心距不大于6,求: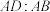 的取值范围.
的取值范围.
 中,点D,E分别为射线
中,点D,E分别为射线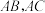 上的动点,
上的动点,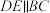 .
.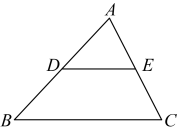
 中点,点E为
中点,点E为 中点时,不借助相似证明中位线性质,求证:
中点时,不借助相似证明中位线性质,求证: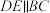 且
且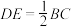 ;
;②若
 面积为25,
面积为25, 变成为10,将
变成为10,将 沿
沿 翻折,设点A落在四边形
翻折,设点A落在四边形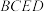 内部的点Q处,设
内部的点Q处,设 为x,
为x,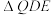 的面积为y,求:y关于x的函数解析式及其定义域;
的面积为y,求:y关于x的函数解析式及其定义域;(2)若当点D,E在边
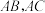 上时,且
上时,且 ,
, 和
和 的重心距为2,当点D,E分别在
的重心距为2,当点D,E分别在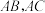 延长线上时,
延长线上时, 与
与 重心距不大于6,求:
重心距不大于6,求: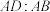 的取值范围.
的取值范围.
您最近一年使用:0次
名校
2 . 如图, 是
是 的直径,
的直径, 平分
平分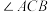 交
交 于点
于点 ,点
,点 在
在 的延长线上,满足
的延长线上,满足 .
. 与
与 相切;
相切;
(2)在下列两个等式中,正确的请在相应的括号中打“√”,错误的打“×”,并选择其中一个正确的等式进行证明;
①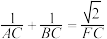 ( );②
( );②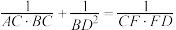 ( );
( );
(3)设 的面积为
的面积为 ,
, 的面积为
的面积为 ,若
,若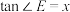 ,
,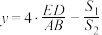 ,试求
,试求 关于
关于 的函数关系式,并求当
的函数关系式,并求当 为何值时,
为何值时, 的值最大.
的值最大.
 是
是 的直径,
的直径, 平分
平分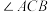 交
交 于点
于点 ,点
,点 在
在 的延长线上,满足
的延长线上,满足 .
.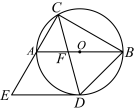
 与
与 相切;
相切;(2)在下列两个等式中,正确的请在相应的括号中打“√”,错误的打“×”,并选择其中一个正确的等式进行证明;
①
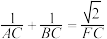 ( );②
( );②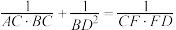 ( );
( );(3)设
 的面积为
的面积为 ,
, 的面积为
的面积为 ,若
,若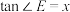 ,
,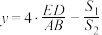 ,试求
,试求 关于
关于 的函数关系式,并求当
的函数关系式,并求当 为何值时,
为何值时, 的值最大.
的值最大.
您最近一年使用:0次
名校
3 . 如图(1),在 中,
中, .点D是
.点D是 边上任意一点(不与B,C重合),连接
边上任意一点(不与B,C重合),连接 ,过点D作
,过点D作 于点E,连接
于点E,连接 ,点F为
,点F为 中点,连接
中点,连接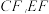 .
.

(1)当 时,判断四边形
时,判断四边形 的形状,并证明.
的形状,并证明.
(2)点D在线段 上的什么位置时,
上的什么位置时,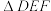 的面积最大?请说明理由.
的面积最大?请说明理由.
(3)如图(1)中的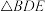 绕点B旋转到如图(2)所示位置,得到
绕点B旋转到如图(2)所示位置,得到 ,使得点A在直线
,使得点A在直线 上,连接
上,连接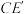 ,点
,点 为
为 中点,
中点, 与
与 交于点G,其他条件不变.求证:
交于点G,其他条件不变.求证: .
.
 中,
中, .点D是
.点D是 边上任意一点(不与B,C重合),连接
边上任意一点(不与B,C重合),连接 ,过点D作
,过点D作 于点E,连接
于点E,连接 ,点F为
,点F为 中点,连接
中点,连接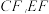 .
.
(1)当
 时,判断四边形
时,判断四边形 的形状,并证明.
的形状,并证明.(2)点D在线段
 上的什么位置时,
上的什么位置时,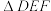 的面积最大?请说明理由.
的面积最大?请说明理由.(3)如图(1)中的
 绕点B旋转到如图(2)所示位置,得到
绕点B旋转到如图(2)所示位置,得到 ,使得点A在直线
,使得点A在直线 上,连接
上,连接 ,点
,点 为
为 中点,
中点, 与
与 交于点G,其他条件不变.求证:
交于点G,其他条件不变.求证: .
.
您最近一年使用:0次
4 . “关联”是解决数学问题的重要思维方式.角平分线的有关联想就有很多……
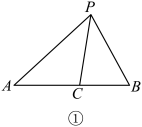
(1)如图①, 是
是 的角平分线,求证
的角平分线,求证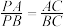 .
.
请根据小明或小红的思路,选择一种并完成证明.
【作图应用】
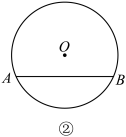
(2)如图②, 是
是 的弦,在
的弦,在 上作出点P,使得
上作出点P,使得 .
.
要求:(1)用直尺和圆规作图;(2)保留作图的痕迹,写出必要的文字说明.
【深度思考】
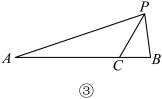
(3)如图③, 是
是 的角平分线,若
的角平分线,若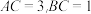 ,则
,则 的面积最大值是______.
的面积最大值是______.
(1)如图①,
 是
是 的角平分线,求证
的角平分线,求证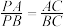 .
.| 小明思路:关联“平行线、等腰三角形”,利用“三角形相似”. 小红思路:关联“角平分线上的点到角的两边的距离相等”,利用“等面积法”. |

【作图应用】
(2)如图②,
 是
是 的弦,在
的弦,在 上作出点P,使得
上作出点P,使得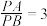 .
.要求:(1)用直尺和圆规作图;(2)保留作图的痕迹,写出必要的文字说明.

【深度思考】
(3)如图③,
 是
是 的角平分线,若
的角平分线,若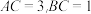 ,则
,则 的面积最大值是______.
的面积最大值是______.
您最近一年使用:0次
2023-02-18更新
|
719次组卷
|
5卷引用:江苏省南京市联合体2022-2023学年九年级上学期期末数学试题
江苏省南京市联合体2022-2023学年九年级上学期期末数学试题江苏省南京市六合区2022-2023学年九年级上学期期末数学试题2023年江苏省宿迁市中考一模数学试题江苏省盐城市2023-2024学年九年级上学期期末数学试题(已下线)专题09圆的有关位置关系及计算1(十大类型)-【好题汇编】备战2023-2024学年九年级数学上学期期末真题分类汇编(苏科版)
名校
5 . 阅读材料:
①对于任意实数 和
和 ,都有
,都有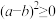 ,∴
,∴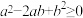 ,于是得到
,于是得到 ,
,
当且仅当 时,等号成立.
时,等号成立.
②任意一个非负实数都可写成一个数的平方的形式.即:如果 ,则
,则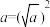 .
.
如: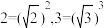 等.
等.
例:已知 ,求证:
,求证: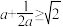 .
.
证明:∵ ,∴
,∴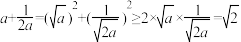
∴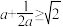 ,当且仅当
,当且仅当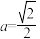 时,等号成立.
时,等号成立.
请阅读上述材料并解答下列问题:如图,某园艺公司准备围建一个矩形花圃,其中一边靠墙(墙的最大可用长度为14米),中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在 上用其他材料做了宽为1米的两扇小门.
上用其他材料做了宽为1米的两扇小门.

(1)若所用的篱笆长为22米.
①若花圃的面积刚好为45平方米,则此时花圃的 段长为多少?
段长为多少?
②当 长为多少米时,这个花圃的面积最大?并求出最大面积;
长为多少米时,这个花圃的面积最大?并求出最大面积;
(2)若要围成面积为75平方米的花圃,需要用的篱笆最少是多少米?
①对于任意实数
 和
和 ,都有
,都有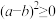 ,∴
,∴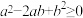 ,于是得到
,于是得到 ,
,当且仅当
 时,等号成立.
时,等号成立.②任意一个非负实数都可写成一个数的平方的形式.即:如果
 ,则
,则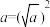 .
.如:
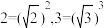 等.
等.例:已知
 ,求证:
,求证: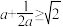 .
.证明:∵
 ,∴
,∴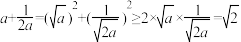
∴
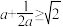 ,当且仅当
,当且仅当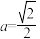 时,等号成立.
时,等号成立.请阅读上述材料并解答下列问题:如图,某园艺公司准备围建一个矩形花圃,其中一边靠墙(墙的最大可用长度为14米),中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在
 上用其他材料做了宽为1米的两扇小门.
上用其他材料做了宽为1米的两扇小门.
(1)若所用的篱笆长为22米.
①若花圃的面积刚好为45平方米,则此时花圃的
 段长为多少?
段长为多少?②当
 长为多少米时,这个花圃的面积最大?并求出最大面积;
长为多少米时,这个花圃的面积最大?并求出最大面积;(2)若要围成面积为75平方米的花圃,需要用的篱笆最少是多少米?
您最近一年使用:0次
名校
6 . 【问题发现】
(1)如图①,在正方形 中,
中, 是
是 上一点(点
上一点(点 与
与 ,
, 不重合),
不重合), 交
交 于点
于点 ,
, 交
交 于点
于点 .试猜想线段
.试猜想线段 ,
, 和
和 之间的数量关系,并证明;
之间的数量关系,并证明;
【延伸探究】
(2)在其余条件不变的基础上延长 ,交
,交 于点
于点 ,连接
,连接 ,
,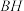 ,交于点
,交于点 ,如图②.求证:
,如图②.求证: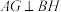 ;
;
【问题解决】
(3)如图③,是一块边长为 米的正方形钢板
米的正方形钢板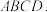 由于磨损,该钢板的顶点
由于磨损,该钢板的顶点 ,
, ,
, 均不能使用,王师傅计划过点
均不能使用,王师傅计划过点 裁出一个形如四边形
裁出一个形如四边形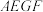 的零件,其中点
的零件,其中点 ,
, ,
, 分别在
分别在 ,
, ,
, 边上,且
边上,且 为
为 的中点,
的中点, 交
交 于点
于点 ,连接
,连接 ,求王师傅能裁出四边形
,求王师傅能裁出四边形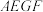 的最大面积是多少?
的最大面积是多少?

(1)如图①,在正方形
 中,
中, 是
是 上一点(点
上一点(点 与
与 ,
, 不重合),
不重合), 交
交 于点
于点 ,
, 交
交 于点
于点 .试猜想线段
.试猜想线段 ,
, 和
和 之间的数量关系,并证明;
之间的数量关系,并证明;【延伸探究】
(2)在其余条件不变的基础上延长
 ,交
,交 于点
于点 ,连接
,连接 ,
,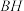 ,交于点
,交于点 ,如图②.求证:
,如图②.求证: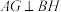 ;
;【问题解决】
(3)如图③,是一块边长为
 米的正方形钢板
米的正方形钢板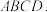 由于磨损,该钢板的顶点
由于磨损,该钢板的顶点 ,
, ,
, 均不能使用,王师傅计划过点
均不能使用,王师傅计划过点 裁出一个形如四边形
裁出一个形如四边形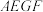 的零件,其中点
的零件,其中点 ,
, ,
, 分别在
分别在 ,
, ,
, 边上,且
边上,且 为
为 的中点,
的中点, 交
交 于点
于点 ,连接
,连接 ,求王师傅能裁出四边形
,求王师傅能裁出四边形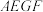 的最大面积是多少?
的最大面积是多少?
您最近一年使用:0次
7 . 阅读材料:
①对于任意实数a和b,都有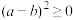 ,∴
,∴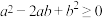 ,得到
,得到 ,当且仅当
,当且仅当 时,等号成立.
时,等号成立.
②任意一个非负实数都可写成一个数的平方的形式.即:如果a≥0,则 .如:
.如: 等.
等.
例:①用配方法求代数式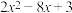 的最小值.
的最小值.
②已知 ,求证:
,求证: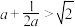 .
.
①解:由题意得: ,
,
∵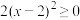 ,且当
,且当 时,
时,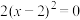 ,
,
∴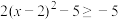 ,
,
∴当 时,代数式
时,代数式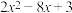 的最小值为:
的最小值为: ;
;
②证明:∵ ,∴
,∴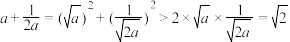
∴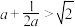 ,当且仅当
,当且仅当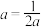 ,即
,即 时,等号成立.
时,等号成立.
请解答下列问题:某园艺公司准备围建一个矩形花圃,其中一边靠墙(墙足够长),另外三边用篱笆围成(如图所示).设垂直于墙的一边长为x米.

(1)若所用的篱笆长为36米,那么:
①当花圃的面积为144平方米时,垂直于墙的一边的长为多少米?
②设花圃的面积为S米 ,求当垂直于墙的一边的长为多少米时,这个花圃的面积最大?并求出这个最大面积;
,求当垂直于墙的一边的长为多少米时,这个花圃的面积最大?并求出这个最大面积;
(2)若要围成面积为200平方米的花圃,需要用的篱笆最少是多少米?
①对于任意实数a和b,都有
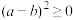 ,∴
,∴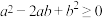 ,得到
,得到 ,当且仅当
,当且仅当 时,等号成立.
时,等号成立.②任意一个非负实数都可写成一个数的平方的形式.即:如果a≥0,则
 .如:
.如: 等.
等.例:①用配方法求代数式
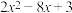 的最小值.
的最小值.②已知
 ,求证:
,求证: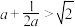 .
.①解:由题意得:
 ,
,∵
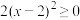 ,且当
,且当 时,
时,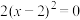 ,
,∴
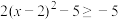 ,
,∴当
 时,代数式
时,代数式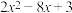 的最小值为:
的最小值为: ;
;②证明:∵
 ,∴
,∴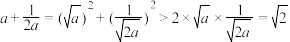
∴
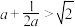 ,当且仅当
,当且仅当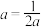 ,即
,即 时,等号成立.
时,等号成立.请解答下列问题:某园艺公司准备围建一个矩形花圃,其中一边靠墙(墙足够长),另外三边用篱笆围成(如图所示).设垂直于墙的一边长为x米.

(1)若所用的篱笆长为36米,那么:
①当花圃的面积为144平方米时,垂直于墙的一边的长为多少米?
②设花圃的面积为S米
 ,求当垂直于墙的一边的长为多少米时,这个花圃的面积最大?并求出这个最大面积;
,求当垂直于墙的一边的长为多少米时,这个花圃的面积最大?并求出这个最大面积;(2)若要围成面积为200平方米的花圃,需要用的篱笆最少是多少米?
您最近一年使用:0次
2022-10-13更新
|
128次组卷
|
2卷引用:广东省深圳市坪山区2022-2023学年九年级上学期学情监测数学试题(9月)
名校
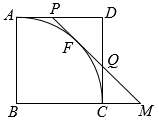
8 . 在边长为1的正方形 中,以点
中,以点 为圆心,
为圆心,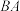 为半径作弧
为半径作弧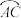 ,
, 为
为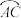 上的一动点,过点
上的一动点,过点 作⊙
作⊙ 的切线交
的切线交 于点
于点 ,交
,交 于点
于点 ,交
,交 的延长线于点
的延长线于点 .
.
(1)当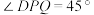 时,求证:点
时,求证:点 为线段
为线段 的中点;
的中点;
(2)设 长为x,
长为x, 长为y,求y关于x的函数关系式;
长为y,求y关于x的函数关系式;
(3)将△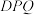 沿直线
沿直线 翻折后得△
翻折后得△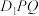 ,当
,当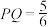 时,△
时,△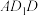 与△
与△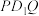 是否相似?如果相似,请加以证明;如果不相似,写出理由.
是否相似?如果相似,请加以证明;如果不相似,写出理由.
 中,以点
中,以点 为圆心,
为圆心,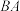 为半径作弧
为半径作弧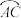 ,
, 为
为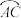 上的一动点,过点
上的一动点,过点 作⊙
作⊙ 的切线交
的切线交 于点
于点 ,交
,交 于点
于点 ,交
,交 的延长线于点
的延长线于点 .
.
(1)当
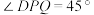 时,求证:点
时,求证:点 为线段
为线段 的中点;
的中点;(2)设
 长为x,
长为x, 长为y,求y关于x的函数关系式;
长为y,求y关于x的函数关系式;(3)将△
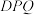 沿直线
沿直线 翻折后得△
翻折后得△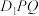 ,当
,当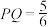 时,△
时,△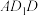 与△
与△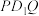 是否相似?如果相似,请加以证明;如果不相似,写出理由.
是否相似?如果相似,请加以证明;如果不相似,写出理由.
您最近一年使用:0次
2022-05-21更新
|
294次组卷
|
2卷引用:2022年湖南省长沙市岳麓区初中学业水平考试模拟(一模)数学试题
9 . 如图,在△ABC中,∠BAC=90°,AD是BC边上的高,E是BC边上的一个动点(不与B,C重合),EF⊥AB,EG⊥AC,垂足分别为F,G.
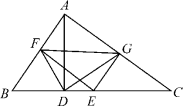
(1)求证: ;
;
(2)FD与DG是否垂直?若垂直,请给出证明;若不垂直,请说明理由;
(3)若AB=6,AC=8,设BE= ,△AFG的面积为
,△AFG的面积为 ,求
,求 与
与 的函数关系式;当
的函数关系式;当 为何值时,
为何值时, 最大?这个最大值是多少?
最大?这个最大值是多少?

(1)求证:
 ;
;(2)FD与DG是否垂直?若垂直,请给出证明;若不垂直,请说明理由;
(3)若AB=6,AC=8,设BE=
 ,△AFG的面积为
,△AFG的面积为 ,求
,求 与
与 的函数关系式;当
的函数关系式;当 为何值时,
为何值时, 最大?这个最大值是多少?
最大?这个最大值是多少?
您最近一年使用:0次
10 . 定义:若一个三角形存在两个内角之差是第三个内角的两倍,则称这个三角形为关于第三个内角的“差倍角三角形”.例如,在 中,
中,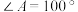 ,
, ,
, ,满足
,满足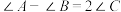 ,所以
,所以 是关于
是关于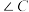 的“差倍角三角形”.
的“差倍角三角形”.
(1)若等腰 是“差倍角三角形”,求等腰三角形的顶角
是“差倍角三角形”,求等腰三角形的顶角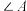 的度数;
的度数;
(2)如图1, 中,
中, ,
,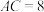 ,
,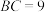 ,小明发现这个
,小明发现这个 是关于
是关于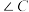 的“差倍角三角形”.
的“差倍角三角形”.
他的证明方法如下:
证明:在 上取点
上取点 ,使得
,使得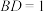 ,连结
,连结 ,(请你完成接下去的证明)
,(请你完成接下去的证明)
(3)如图2,五边形 内接于圆,连结
内接于圆,连结 ,
, 与
与 相交于点
相交于点 ,
, ,
,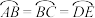 ,
,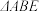 是关于
是关于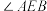 的“差倍角三角形”.
的“差倍角三角形”.
①求证:四边形 是平行四边形;
是平行四边形;
②若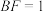 ,设
,设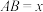 ,
,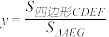 ,求
,求 关于
关于 的函数关系式.
的函数关系式.

 中,
中,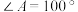 ,
, ,
, ,满足
,满足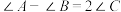 ,所以
,所以 是关于
是关于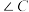 的“差倍角三角形”.
的“差倍角三角形”.(1)若等腰
 是“差倍角三角形”,求等腰三角形的顶角
是“差倍角三角形”,求等腰三角形的顶角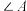 的度数;
的度数;(2)如图1,
 中,
中, ,
,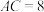 ,
,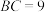 ,小明发现这个
,小明发现这个 是关于
是关于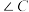 的“差倍角三角形”.
的“差倍角三角形”.他的证明方法如下:
证明:在
 上取点
上取点 ,使得
,使得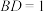 ,连结
,连结 ,(请你完成接下去的证明)
,(请你完成接下去的证明)(3)如图2,五边形
 内接于圆,连结
内接于圆,连结 ,
, 与
与 相交于点
相交于点 ,
, ,
,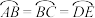 ,
,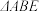 是关于
是关于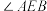 的“差倍角三角形”.
的“差倍角三角形”.①求证:四边形
 是平行四边形;
是平行四边形;②若
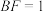 ,设
,设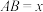 ,
,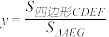 ,求
,求 关于
关于 的函数关系式.
的函数关系式.
您最近一年使用:0次
2021-02-25更新
|
425次组卷
|
5卷引用:浙江省宁波市鄞州区2020-2021学年九年级上学期期末数学试题
浙江省宁波市鄞州区2020-2021学年九年级上学期期末数学试题2021年福建省龙岩市部分学校中考数学第一次适应性试卷(一)(已下线)【新东方】【2021.5.25】【NB】【初三上】【数学】【NB00021】浙江省宁波市各地区2020-2021学年九年级上学期数学期末大题难题汇编(已下线)期末难点特训(二)与相似三角形有关的压轴题-【微专题】2022-2023学年九年级数学下册常考点微专题提分精练(浙教版)



