名校
1 . 已知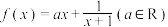 .
.
(1)当 时,求不等式
时,求不等式 的解集;
的解集;
(2)若 时,
时, 有零点,求
有零点,求 的范围.
的范围.
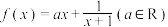 .
.(1)当
 时,求不等式
时,求不等式 的解集;
的解集;(2)若
 时,
时, 有零点,求
有零点,求 的范围.
的范围.
您最近一年使用:0次
2023-10-16更新
|
501次组卷
|
10卷引用:上海市莘庄中学2019-2020学年高一上学期12月月考数学试题
上海市莘庄中学2019-2020学年高一上学期12月月考数学试题上海市2022届高三模拟(三)数学试题(已下线)专题3-6 导数综合大题:零点与求参及不等式证明 -24.5.1+4.5.2函数模型及其应用江苏省兴化市楚水实验学校、兴化一中等四校2023-2024学年高三上学期第一次阶段测试数学试题(已下线)4.5.1&4.5.2 函数的零点与方程的解、用二分法求方程的近似解数学同步精品课堂(人教A版2019必修第一册)宁夏银川市第二中学2023-2024学年高一上学期月考二数学试卷(已下线)专题04 函数解答题(3类题型 理科)(已下线)专题19 函数解答题(文科)上海市民办尚德实验学校2023-2024学年高二下学期期末考试数学试卷
名校
2 . 已知关于 的函数
的函数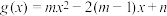 为
为 上的偶函数,且在区间
上的偶函数,且在区间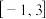 上的最大值为10.设
上的最大值为10.设 .
.
(1)求函数 的解析式.
的解析式.
(2)若不等式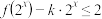 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
(3)是否存在实数 ,使得关于
,使得关于 的方程
的方程 有四个不相等的实数根?如果存在,求出实数
有四个不相等的实数根?如果存在,求出实数 的范围,如果不存在,说明理由.
的范围,如果不存在,说明理由.
 的函数
的函数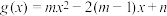 为
为 上的偶函数,且在区间
上的偶函数,且在区间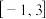 上的最大值为10.设
上的最大值为10.设 .
.(1)求函数
 的解析式.
的解析式.(2)若不等式
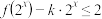 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.(3)是否存在实数
 ,使得关于
,使得关于 的方程
的方程 有四个不相等的实数根?如果存在,求出实数
有四个不相等的实数根?如果存在,求出实数 的范围,如果不存在,说明理由.
的范围,如果不存在,说明理由.
您最近一年使用:0次
2020-12-26更新
|
2494次组卷
|
8卷引用:江苏省扬州市2017~2018学年度高一第一学期期末调研测试数学试题
名校
3 . 设 且
且 ,函数
,函数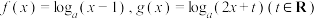 .
.
(1)当 时,求不等式
时,求不等式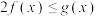 的解集;
的解集;
(2)若函数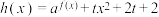 在区间
在区间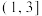 上有零点,求
上有零点,求 的取值范围.
的取值范围.
 且
且 ,函数
,函数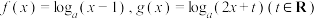 .
.(1)当
 时,求不等式
时,求不等式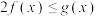 的解集;
的解集;(2)若函数
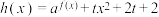 在区间
在区间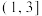 上有零点,求
上有零点,求 的取值范围.
的取值范围.
您最近一年使用:0次
2024-09-27更新
|
666次组卷
|
6卷引用:2025届河南省部分重点高中高三九师联盟模拟预测数学试题
2025届河南省部分重点高中高三九师联盟模拟预测数学试题天津市南开中学2025届高三上学期10月月考数学试题(已下线)第05节 构造函数或构造方程解题的技巧【练】高三数学思想大全(已下线)第06节 运用函数与方程思想方法解题过程中的三大法宝【讲】高三数学思想大全2025届宁夏高三上学期10月新起点调研数学模拟试卷(二)·江苏省苏州工业园区星海实验中学2025届高三上学期10月月考数学试题
4 . 已知函数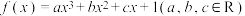 ,且不等式
,且不等式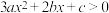 的解集为
的解集为 .
.
(1)求函数 图象的对称中心;
图象的对称中心;
(2)证明:函数 在区间
在区间 上单调递增;
上单调递增;
(3)若方程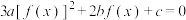 有6个不相等的实数根,求实数
有6个不相等的实数根,求实数 的取值范围.
的取值范围.
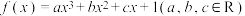 ,且不等式
,且不等式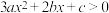 的解集为
的解集为 .
.(1)求函数
 图象的对称中心;
图象的对称中心;(2)证明:函数
 在区间
在区间 上单调递增;
上单调递增;(3)若方程
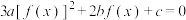 有6个不相等的实数根,求实数
有6个不相等的实数根,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
5 . 定义三阶行列式运算: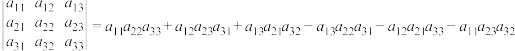 ,其中
,其中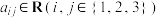 .已知
.已知 ,关于
,关于 的不等式
的不等式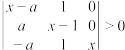 的解集为
的解集为 .
.
(1)求 ;
;
(2)已知函数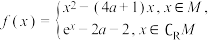 不存在最小值,求
不存在最小值,求 的取值范围.
的取值范围.
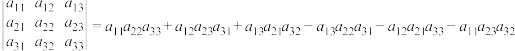 ,其中
,其中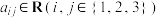 .已知
.已知 ,关于
,关于 的不等式
的不等式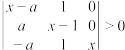 的解集为
的解集为 .
.(1)求
 ;
;(2)已知函数
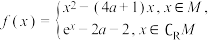 不存在最小值,求
不存在最小值,求 的取值范围.
的取值范围.
您最近一年使用:0次
名校
6 . 已知函数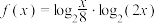 ,函数
,函数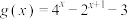 .
.
(1)求不等式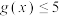 的解集;
的解集;
(2)求函数 的值域;
的值域;
(3)若不等式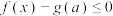 对任意实数
对任意实数 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.
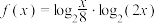 ,函数
,函数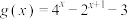 .
.(1)求不等式
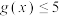 的解集;
的解集;(2)求函数
 的值域;
的值域;(3)若不等式
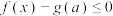 对任意实数
对任意实数 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.
您最近一年使用:0次
7 . 已知函数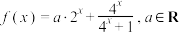 .
.
(1)当 时,求不等式
时,求不等式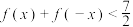 的解集;
的解集;
(2)若函数 有零点,求
有零点,求 的取值范围.
的取值范围.
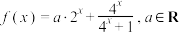 .
.(1)当
 时,求不等式
时,求不等式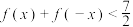 的解集;
的解集;(2)若函数
 有零点,求
有零点,求 的取值范围.
的取值范围.
您最近一年使用:0次
8 . 定义一种新的运算“ ”
”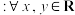 ,都有
,都有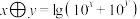 .
.
(1)对于任意实数 ,试判断
,试判断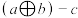 与
与 的大小关系;
的大小关系;
(2)若关于 的不等式
的不等式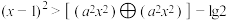 的解集中的整数恰有2个,求实数
的解集中的整数恰有2个,求实数 的取值范围;
的取值范围;
(3)已知函数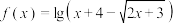 ,
, ,若对任意的
,若对任意的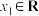 ,总存在
,总存在 ,使得
,使得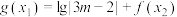 ,求实数
,求实数 的取值范围.
的取值范围.
 ”
”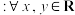 ,都有
,都有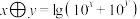 .
.(1)对于任意实数
 ,试判断
,试判断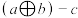 与
与 的大小关系;
的大小关系;(2)若关于
 的不等式
的不等式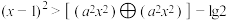 的解集中的整数恰有2个,求实数
的解集中的整数恰有2个,求实数 的取值范围;
的取值范围;(3)已知函数
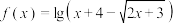 ,
, ,若对任意的
,若对任意的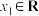 ,总存在
,总存在 ,使得
,使得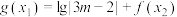 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
9 . 已知函数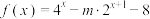 .
.
(1)若 ,求不等式
,求不等式 的解集;
的解集;
(2)若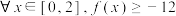 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
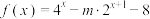 .
.(1)若
 ,求不等式
,求不等式 的解集;
的解集;(2)若
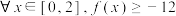 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2024-07-22更新
|
1058次组卷
|
5卷引用:内蒙古呼和浩特铁路局呼和浩特职工子弟第一中学2022-2023学年高二下学期期末考试数学试卷
内蒙古呼和浩特铁路局呼和浩特职工子弟第一中学2022-2023学年高二下学期期末考试数学试卷(已下线)核心考点10 函数(一轮复习) A基础卷 (高二期末考试必考的10大核心考点)(已下线)【高二模块二】类型5 以函数为背景的解答题(A卷基础卷)辽宁省鞍山市2023-2024学年高二下学期期末考试数学试卷湖南省长沙市2023-2024学年高一下学期期末数学试题
名校
解题方法
10 . 已知函数 ,且
,且 .
.
(1)解不等式 ;
;
(2)设不等式 的解集为集合
的解集为集合 ,若对任意
,若对任意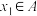 ,存在
,存在 ,使得
,使得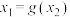 ,求实数
,求实数 的取值范围.
的取值范围.
 ,且
,且 .
.(1)解不等式
 ;
;(2)设不等式
 的解集为集合
的解集为集合 ,若对任意
,若对任意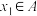 ,存在
,存在 ,使得
,使得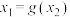 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2024-01-06更新
|
895次组卷
|
8卷引用:河南省新高中创新联盟TOP二十名校2023-2024学年高一上学期1月调研考试数学试题
河南省新高中创新联盟TOP二十名校2023-2024学年高一上学期1月调研考试数学试题江西省上饶市广丰贞白中学2024届高三上学期1月考试数学试题(已下线)第14题 对数不等 单调优先(已下线)专题04 指数函数与对数函数4-2024年高一数学寒假作业单元合订本安徽省阜阳市2023-2024学年高一上学期期末联考数学试卷辽宁省本溪市第一中学2023-2024学年高一下学期寒假验收考试数学试题江西省部分学校2023-2024学年高一上学期1月期末教学质量检测数学试题广东省茂名市高州市第一中学2023-2024学年高一下学期开学考试数学试题



