名校
解题方法
1 . 设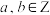 ,
, .如果存在
.如果存在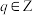 使得
使得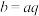 ,那么就说
,那么就说 可被
可被 整除(或
整除(或 整除
整除 ),记做
),记做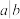 且称
且称 是
是 的倍数,
的倍数, 是
是 的约数(也可称为除数、因数).
的约数(也可称为除数、因数). 不能被
不能被 整除就记做
整除就记做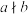 .由整除的定义,不难得出整除的下面几条性质:①若
.由整除的定义,不难得出整除的下面几条性质:①若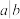 ,
,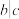 ,则
,则 ;②
;② ,
, 互质,若
互质,若 ,
,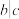 ,则
,则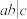 ;③若
;③若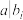 ,则
,则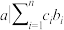 ,其中
,其中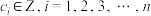 .
.
(1)若数列 满足,
满足,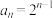 ,其前
,其前 项和为
项和为 ,证明:
,证明: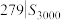 ;
;
(2)若 为奇数,求证:
为奇数,求证: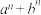 能被
能被 整除;
整除;
(3)对于整数 与
与 ,
,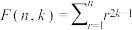 ,求证:
,求证: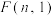 可整除
可整除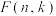 .
.
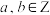 ,
, .如果存在
.如果存在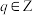 使得
使得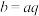 ,那么就说
,那么就说 可被
可被 整除(或
整除(或 整除
整除 ),记做
),记做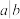 且称
且称 是
是 的倍数,
的倍数, 是
是 的约数(也可称为除数、因数).
的约数(也可称为除数、因数). 不能被
不能被 整除就记做
整除就记做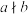 .由整除的定义,不难得出整除的下面几条性质:①若
.由整除的定义,不难得出整除的下面几条性质:①若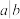 ,
,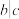 ,则
,则 ;②
;② ,
, 互质,若
互质,若 ,
,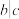 ,则
,则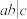 ;③若
;③若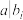 ,则
,则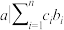 ,其中
,其中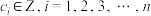 .
.(1)若数列
 满足,
满足,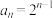 ,其前
,其前 项和为
项和为 ,证明:
,证明: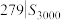 ;
;(2)若
 为奇数,求证:
为奇数,求证: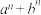 能被
能被 整除;
整除;(3)对于整数
 与
与 ,
,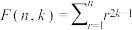 ,求证:
,求证: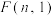 可整除
可整除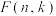 .
.
您最近一年使用:0次
2024-05-19更新
|
544次组卷
|
2卷引用:山东中学联盟2024届高考考前热身押题数学试题
2 . 如图所示数阵,第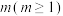 行共有
行共有 个数,第
个数,第 行的第1个数为
行的第1个数为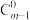 ,第2个数为
,第2个数为 ,第
,第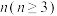 个数为
个数为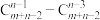 .规定:
.规定: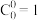 .
.

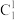
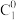
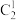


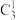
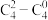

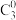
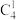


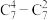
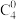
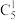
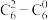

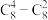
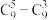

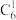
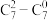

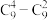
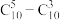
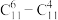

(1)试判断每一行的最后两个数的大小关系,并证明你的结论;
(2)求证:每一行的所在数之和等于下一行的最后一个数;
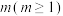 行共有
行共有 个数,第
个数,第 行的第1个数为
行的第1个数为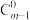 ,第2个数为
,第2个数为 ,第
,第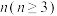 个数为
个数为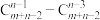 .规定:
.规定: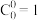 .
.
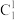
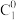
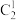


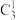
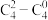

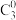
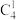


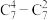
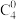
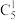
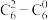

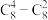
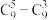

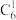
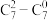

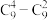
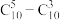
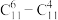

(1)试判断每一行的最后两个数的大小关系,并证明你的结论;
(2)求证:每一行的所在数之和等于下一行的最后一个数;
您最近一年使用:0次
3 . 在足球比赛中,有时需通过点球决定胜负.
(1)扑点球的难度一般比较大,假设罚点球的球员会等可能地随机选择球门的左、中、右三个方向射门,门将(也称为守门员)也会等可能地随机选择球门的左、中、右三个方向来扑点球,而且门将即使方向判断正确也有 的可能性扑不到球.不考虑其它因素,在一次点球大战中,求门将在前三次扑到点球的个数
的可能性扑不到球.不考虑其它因素,在一次点球大战中,求门将在前三次扑到点球的个数 的分布列和期望;
的分布列和期望;
(2)好成绩的取得离不开平时的努力训练,甲、乙、丙三名前锋队员在某次传接球的训练中,球从甲脚下开始,等可能地随机传向另外 人中的
人中的  人,接球者接到球后再等可能地随机传向另外
人,接球者接到球后再等可能地随机传向另外 人中的
人中的 人,如此不停地传下去,假设传出的球都能接住.记第
人,如此不停地传下去,假设传出的球都能接住.记第 次传球之前球在甲脚下的概率为
次传球之前球在甲脚下的概率为 ,易知
,易知 .
.
① 试证明: 为等比数列;
为等比数列;
② 设第 次传球之前球在乙脚下的概率为
次传球之前球在乙脚下的概率为 ,比较
,比较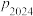 与
与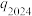 的大小.
的大小.
(1)扑点球的难度一般比较大,假设罚点球的球员会等可能地随机选择球门的左、中、右三个方向射门,门将(也称为守门员)也会等可能地随机选择球门的左、中、右三个方向来扑点球,而且门将即使方向判断正确也有
 的可能性扑不到球.不考虑其它因素,在一次点球大战中,求门将在前三次扑到点球的个数
的可能性扑不到球.不考虑其它因素,在一次点球大战中,求门将在前三次扑到点球的个数 的分布列和期望;
的分布列和期望;(2)好成绩的取得离不开平时的努力训练,甲、乙、丙三名前锋队员在某次传接球的训练中,球从甲脚下开始,等可能地随机传向另外
 人中的
人中的  人,接球者接到球后再等可能地随机传向另外
人,接球者接到球后再等可能地随机传向另外 人中的
人中的 人,如此不停地传下去,假设传出的球都能接住.记第
人,如此不停地传下去,假设传出的球都能接住.记第 次传球之前球在甲脚下的概率为
次传球之前球在甲脚下的概率为 ,易知
,易知 .
.① 试证明:
 为等比数列;
为等比数列;② 设第
 次传球之前球在乙脚下的概率为
次传球之前球在乙脚下的概率为 ,比较
,比较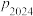 与
与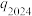 的大小.
的大小.
您最近一年使用:0次
名校
解题方法
4 . 数列 中,从第二项起,每一项与其前一项的差组成的数列
中,从第二项起,每一项与其前一项的差组成的数列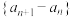 称为
称为 的一阶差数列,记为
的一阶差数列,记为 ,依此类推,
,依此类推, 的一阶差数列称为
的一阶差数列称为 的二阶差数列,记为
的二阶差数列,记为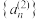 ,….如果一个数列
,….如果一个数列 的p阶差数列
的p阶差数列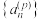 是等比数列,则称数列
是等比数列,则称数列 为p阶等比数列
为p阶等比数列 .
.
(1)已知数列 满足
满足 ,
,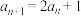 .
.
(ⅰ)求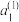 ,
,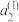 ,
,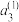 ;
;
(ⅱ)证明: 是一阶等比数列;
是一阶等比数列;
(2)已知数列 为二阶等比数列,其前5项分别为
为二阶等比数列,其前5项分别为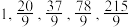 ,求
,求 及满足
及满足 为整数的所有n值.
为整数的所有n值.
 中,从第二项起,每一项与其前一项的差组成的数列
中,从第二项起,每一项与其前一项的差组成的数列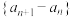 称为
称为 的一阶差数列,记为
的一阶差数列,记为 ,依此类推,
,依此类推, 的一阶差数列称为
的一阶差数列称为 的二阶差数列,记为
的二阶差数列,记为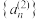 ,….如果一个数列
,….如果一个数列 的p阶差数列
的p阶差数列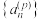 是等比数列,则称数列
是等比数列,则称数列 为p阶等比数列
为p阶等比数列 .
.(1)已知数列
 满足
满足 ,
,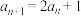 .
.(ⅰ)求
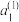 ,
,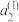 ,
,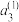 ;
;(ⅱ)证明:
 是一阶等比数列;
是一阶等比数列;(2)已知数列
 为二阶等比数列,其前5项分别为
为二阶等比数列,其前5项分别为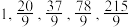 ,求
,求 及满足
及满足 为整数的所有n值.
为整数的所有n值.
您最近一年使用:0次
2024-05-07更新
|
992次组卷
|
5卷引用:2024届山东省潍坊市二模数学试题
2024届山东省潍坊市二模数学试题北京市中国人民大学附属中学2023-2024学年高二下学期统练3数学试题吉林市第一中学2024届高三高考适应性训练(二)数学试题(已下线)专题04 高二下期末考前必刷卷02(提高卷)--高二期末考点大串讲(人教A版2019)2024届吉林省吉林市第一中学高三数学适应性试卷(二)
名校
解题方法
5 . (1)在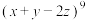 的展开式中,求形如
的展开式中,求形如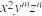 (
( ,
, )的所有项的系数之和.
)的所有项的系数之和.
(2)证明: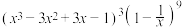 展开式中的常数项为
展开式中的常数项为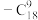 .
.
(3)设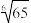 的小数部分为
的小数部分为 ,比较
,比较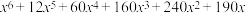 与1的大小
与1的大小
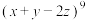 的展开式中,求形如
的展开式中,求形如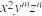 (
( ,
, )的所有项的系数之和.
)的所有项的系数之和.(2)证明:
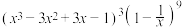 展开式中的常数项为
展开式中的常数项为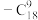 .
.(3)设
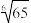 的小数部分为
的小数部分为 ,比较
,比较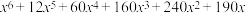 与1的大小
与1的大小
您最近一年使用:0次
7日内更新
|
184次组卷
|
3卷引用:山东省聊城第三中学等校2023-2024学年高二下学期5月质量监测联合调考数学试题
6 . 如图所示数阵,第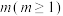 行共有
行共有 个数,第
个数,第 行的第1个数为
行的第1个数为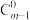 ,第2个数为
,第2个数为 ,第
,第 个数为
个数为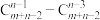 .规定:
.规定: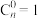 .
.
(2)从第1行起,每一行最后一个数依次构成数列 ,设数列
,设数列 的前
的前 项和为
项和为 ,是否存在正整数
,是否存在正整数 ,使得对任意正整数
,使得对任意正整数 ,
, 恒成立?如存在,请求出
恒成立?如存在,请求出 的最大值;如不存在,请说明理由.
的最大值;如不存在,请说明理由.
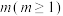 行共有
行共有 个数,第
个数,第 行的第1个数为
行的第1个数为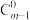 ,第2个数为
,第2个数为 ,第
,第 个数为
个数为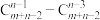 .规定:
.规定: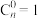 .
.
(2)从第1行起,每一行最后一个数依次构成数列
 ,设数列
,设数列 的前
的前 项和为
项和为 ,是否存在正整数
,是否存在正整数 ,使得对任意正整数
,使得对任意正整数 ,
, 恒成立?如存在,请求出
恒成立?如存在,请求出 的最大值;如不存在,请说明理由.
的最大值;如不存在,请说明理由.
您最近一年使用:0次
名校
7 . 某中学有A,B两个餐厅为老师与学生们提供午餐与晚餐服务,王同学、张老师两人每天午餐和晚餐都在学校就餐,近一个月(30天)选择餐厅就餐情况统计如下:
假设王同学、张老师选择餐厅相互独立,用频率估计概率.
(1)估计一天中王同学午餐和晚餐选择不同餐厅就餐的概率;
(2)记X为王同学、张老师在一天中就餐餐厅的个数,求X的分布列和数学期望 ;
;
(3)假设M表示事件“A餐厅推出优惠套餐”,N表示事件“某学生去A餐厅就餐”,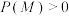 ,已知推出优惠套餐的情况下学生去该餐厅就餐的概率会比不推出优惠套餐的情况下去该餐厅就餐的概率要大,证明.
,已知推出优惠套餐的情况下学生去该餐厅就餐的概率会比不推出优惠套餐的情况下去该餐厅就餐的概率要大,证明. .
.
| 选择餐厅情况(午餐,晚餐) |  | 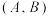 | 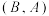 | 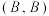 |
| 王同学 | 9天 | 6天 | 12天 | 3天 |
| 张老师 | 6天 | 6天 | 6天 | 12天 |
(1)估计一天中王同学午餐和晚餐选择不同餐厅就餐的概率;
(2)记X为王同学、张老师在一天中就餐餐厅的个数,求X的分布列和数学期望
 ;
;(3)假设M表示事件“A餐厅推出优惠套餐”,N表示事件“某学生去A餐厅就餐”,
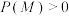 ,已知推出优惠套餐的情况下学生去该餐厅就餐的概率会比不推出优惠套餐的情况下去该餐厅就餐的概率要大,证明.
,已知推出优惠套餐的情况下学生去该餐厅就餐的概率会比不推出优惠套餐的情况下去该餐厅就餐的概率要大,证明. .
.
您最近一年使用:0次
2023-12-14更新
|
1656次组卷
|
8卷引用:山东省济南市山东省实验中学2024届高三上学期第三次诊断考试数学试题
山东省济南市山东省实验中学2024届高三上学期第三次诊断考试数学试题(已下线)模块六 全真模拟篇 拔高2 期末终极研习室(2023-2024学年第一学期)高三江苏省扬州市广陵区红桥高级中学 2024届高三上学期12月月考数学试题山西省运城市盐湖区第五高级中学2024届高三上学期一轮复习成果检测数学试题广东省珠海市第一中学2024届高三上学期期末模拟数学试题(三)(已下线)第01讲 7.1.1条件概率-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)7.1.1 条件概率——课后作业(提升版)(已下线)专题07 概率与统计综合问题(6类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)
8 . 在机器学习中,精确率 、召回率
、召回率 、卡帕系数
、卡帕系数 是衡量算法性能的重要指标.科研机构为了测试某型号扫雷机器人的检测效果,将模拟战场分为100个位点,并在部分位点部署地雷.扫雷机器人依次对每个位点进行检测,
是衡量算法性能的重要指标.科研机构为了测试某型号扫雷机器人的检测效果,将模拟战场分为100个位点,并在部分位点部署地雷.扫雷机器人依次对每个位点进行检测, 表示事件“选到的位点实际有雷”,
表示事件“选到的位点实际有雷”, 表示事件“选到的位点检测到有雷”,定义:精确率
表示事件“选到的位点检测到有雷”,定义:精确率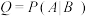 ,召回率
,召回率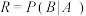 ,卡帕系数
,卡帕系数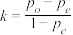 ,其中
,其中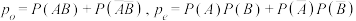 .
.
(1)若某次测试的结果如下表所示,求该扫雷机器人的精确率 和召回率
和召回率 .
.
(2)对任意一次测试,证明: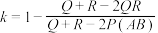 .
.
(3)若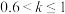 ,则认为机器人的检测效果良好;若
,则认为机器人的检测效果良好;若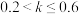 ,则认为检测效果一般;若
,则认为检测效果一般;若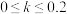 ,则认为检测效果差.根据卡帕系数
,则认为检测效果差.根据卡帕系数 评价(1)中机器人的检测效果.
评价(1)中机器人的检测效果.
 、召回率
、召回率 、卡帕系数
、卡帕系数 是衡量算法性能的重要指标.科研机构为了测试某型号扫雷机器人的检测效果,将模拟战场分为100个位点,并在部分位点部署地雷.扫雷机器人依次对每个位点进行检测,
是衡量算法性能的重要指标.科研机构为了测试某型号扫雷机器人的检测效果,将模拟战场分为100个位点,并在部分位点部署地雷.扫雷机器人依次对每个位点进行检测, 表示事件“选到的位点实际有雷”,
表示事件“选到的位点实际有雷”, 表示事件“选到的位点检测到有雷”,定义:精确率
表示事件“选到的位点检测到有雷”,定义:精确率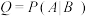 ,召回率
,召回率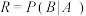 ,卡帕系数
,卡帕系数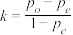 ,其中
,其中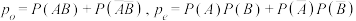 .
.(1)若某次测试的结果如下表所示,求该扫雷机器人的精确率
 和召回率
和召回率 .
.| 实际有雷 | 实际无雷 | 总计 | |
| 检测到有雷 | 40 | 24 | 64 |
| 检测到无雷 | 10 | 26 | 36 |
| 总计 | 50 | 50 | 100 |
(2)对任意一次测试,证明:
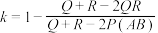 .
.(3)若
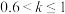 ,则认为机器人的检测效果良好;若
,则认为机器人的检测效果良好;若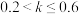 ,则认为检测效果一般;若
,则认为检测效果一般;若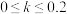 ,则认为检测效果差.根据卡帕系数
,则认为检测效果差.根据卡帕系数 评价(1)中机器人的检测效果.
评价(1)中机器人的检测效果.
您最近一年使用:0次
名校
9 . 某品牌女装专卖店设计摸球抽奖促销活动,每位顾客只用一个会员号登陆,每次消费都有一次随机摸球的机会.已知顾客第一次摸球抽中奖品的概率为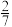 ;从第二次摸球开始,若前一次没抽中奖品,则这次抽中的概率为
;从第二次摸球开始,若前一次没抽中奖品,则这次抽中的概率为 ,若前一次抽中奖品,则这次抽中的概率为
,若前一次抽中奖品,则这次抽中的概率为 .记该顾客第n次摸球抽中奖品的概率为
.记该顾客第n次摸球抽中奖品的概率为 .
.
(1)求
 的值,并探究数列
的值,并探究数列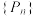 的通项公式;
的通项公式;(2)求该顾客第几次摸球抽中奖品的概率最大,请给出证明过程.
您最近一年使用:0次
2023-10-14更新
|
2040次组卷
|
8卷引用:山东省实验中学2024届高三第一次诊断考试数学试题
山东省实验中学2024届高三第一次诊断考试数学试题浙江省金华十校2023-2024学年高三上学期11月月考模拟数学试题(已下线)山东省实验中学2024届高三第一次诊断考试数学试题变式题19-22(已下线)考点19 概率中的数列 2024届高考数学考点总动员(已下线)专题21 概率与统计的综合运用(13大核心考点)(讲义)(已下线)黄金卷01(2024新题型)重庆市第十一中学校教育集团2024届高三第七次质量检测(3月)数学试题山西省大同市第一中学校2023-2024学年高二下学期3月月考数学试题
解题方法
10 . 为了解学生中午的用餐方式(在食堂就餐或点外卖)与最近食堂间的距离的关系,某大学于某日中午随机调查了2000名学生,获得了下面的频率分布表(不完整),并且由该频率分布表,可估计学生与最近食堂间的平均距离为 (同一组数据以该组数据所在区间的中点值作为代表).
(同一组数据以该组数据所在区间的中点值作为代表).
(1)求出 的值并补全频率分布表;
的值并补全频率分布表;
(2)根据频率分布表补全样本容量为 的
的 列联表(如下表),并根据小概率值
列联表(如下表),并根据小概率值 的独立性检验,能否认为学生中午的用餐方式与学生距最近食堂的远近有关(当学生与最近食堂间的距离不超过
的独立性检验,能否认为学生中午的用餐方式与学生距最近食堂的远近有关(当学生与最近食堂间的距离不超过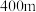 时,认为较近,否则认为较远);
时,认为较近,否则认为较远);
根据频率分布表列出如下的 列联表:
列联表:
(3)一般情况下,学生更愿意去饭菜更美味的食堂就餐.该校距李明较近的有甲、乙两家食堂,且他每天中午都选择食堂甲或乙就餐.记他选择去甲食堂就餐为事件A,他认为甲食堂的饭菜比乙食堂的美味为事件D,且D、A均为随机事件,证明: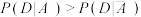 .
.
附: ,其中
,其中 .
.
 (同一组数据以该组数据所在区间的中点值作为代表).
(同一组数据以该组数据所在区间的中点值作为代表).学生与最近食堂间的距离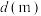 |  | 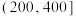 |  | 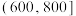 | 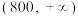 | 合计 |
| 在食堂就餐 | 0.15 | 0.10 | 0.00 | 0.50 | ||
| 点外卖 | 0.20 | 0.00 | 0.50 | |||
| 合计 | 0.20 |
| 0.15 | 0.00 | 1.00 |
 的值并补全频率分布表;
的值并补全频率分布表;(2)根据频率分布表补全样本容量为
 的
的 列联表(如下表),并根据小概率值
列联表(如下表),并根据小概率值 的独立性检验,能否认为学生中午的用餐方式与学生距最近食堂的远近有关(当学生与最近食堂间的距离不超过
的独立性检验,能否认为学生中午的用餐方式与学生距最近食堂的远近有关(当学生与最近食堂间的距离不超过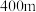 时,认为较近,否则认为较远);
时,认为较近,否则认为较远);根据频率分布表列出如下的
 列联表:
列联表:学生距最近食堂较近 | 学生距最近食堂较远 | 合计 | |
在食堂就餐 | |||
点外卖 | |||
合计 |
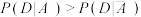 .
.附:
 ,其中
,其中 .
. | 0.10 | 0.010 | 0.001 |
 | 2.706 | 6.635 | 10.828 |
您最近一年使用:0次



