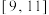名校
解题方法
1 . 十九大提出:坚决打赢脱贫攻坚战,做到精准扶贫.某县积极引导农民种植一种名贵中药材,从而大大提升了该县农民经济收入.2019年年底,某调查机构从该县种植这种名贵中药材的农户中随机抽取了100户,统计了他们2019年种植中药材所获纯利润(单位:万元)的情况,统计结果如下表所示:
(1)该县农户种植中药材所获纯利润 (单位:万元)近似地服从正态分布
(单位:万元)近似地服从正态分布 ,其中
,其中 近似为样本平均数
近似为样本平均数 (每组数据取区间的中点值),
(每组数据取区间的中点值), 近似为样本方差
近似为样本方差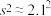 .若该县有1万户农户种植了该中药材,试估算所获纯利润
.若该县有1万户农户种植了该中药材,试估算所获纯利润 在区间
在区间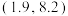 内的户数;
内的户数;
(2)为答谢广大农户的积极参与,该调查机构针对参与调查的农户举行了抽奖活动,抽奖规则如下:在一箱子中放置5个除颜色外完全相同的小球,其中红球1个,黑球4个.让农户从箱子中随机取出一个小球,若取到红球,则停止取球;若取到黑球,则将黑球放回箱中,继续取球,但取球次数不超过10次.若农户取到红球,则中奖,获得2000元的奖励,若未取到红球,则不中奖.现农户张明参加了抽奖活动,记他取球的次数为随机变量 .
.
①求张明恰好取球4次的概率;
②求 的数学期望.(精确到0.001)
的数学期望.(精确到0.001)
参考数据: ,
, .若随机变量
.若随机变量 ,则
,则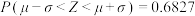 ,
,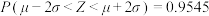 .
.
分组 |
|
|
|
|
|
频数 | 10 | 15 | 45 | 20 | 10 |
(1)该县农户种植中药材所获纯利润
 (单位:万元)近似地服从正态分布
(单位:万元)近似地服从正态分布 ,其中
,其中 近似为样本平均数
近似为样本平均数 (每组数据取区间的中点值),
(每组数据取区间的中点值), 近似为样本方差
近似为样本方差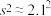 .若该县有1万户农户种植了该中药材,试估算所获纯利润
.若该县有1万户农户种植了该中药材,试估算所获纯利润 在区间
在区间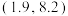 内的户数;
内的户数;(2)为答谢广大农户的积极参与,该调查机构针对参与调查的农户举行了抽奖活动,抽奖规则如下:在一箱子中放置5个除颜色外完全相同的小球,其中红球1个,黑球4个.让农户从箱子中随机取出一个小球,若取到红球,则停止取球;若取到黑球,则将黑球放回箱中,继续取球,但取球次数不超过10次.若农户取到红球,则中奖,获得2000元的奖励,若未取到红球,则不中奖.现农户张明参加了抽奖活动,记他取球的次数为随机变量
 .
.①求张明恰好取球4次的概率;
②求
 的数学期望.(精确到0.001)
的数学期望.(精确到0.001)参考数据:
 ,
, .若随机变量
.若随机变量 ,则
,则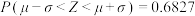 ,
,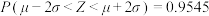 .
.
您最近一年使用:0次
2020-09-12更新
|
507次组卷
|
3卷引用:山东省日照市2020-2021学年高三9月校际联考数学试题
名校
解题方法
2 . 经研究发现:任意一个三次多项式函数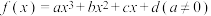 的图象都只有一个对称中心点
的图象都只有一个对称中心点 ,其中
,其中 是
是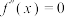 的根,
的根, 是
是 的导数,
的导数, 是
是 的导数.若函数
的导数.若函数 图象的对称点为
图象的对称点为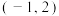 ,且不等式
,且不等式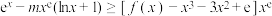 对任意
对任意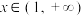 恒成立,则下列结论正确的是( )
恒成立,则下列结论正确的是( )
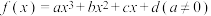 的图象都只有一个对称中心点
的图象都只有一个对称中心点 ,其中
,其中 是
是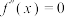 的根,
的根, 是
是 的导数,
的导数, 是
是 的导数.若函数
的导数.若函数 图象的对称点为
图象的对称点为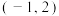 ,且不等式
,且不等式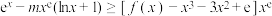 对任意
对任意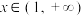 恒成立,则下列结论正确的是( )
恒成立,则下列结论正确的是( )A. | B. | C. 的值可能是 的值可能是 | D. 的值可能是 的值可能是 |
您最近一年使用:0次
2024-01-15更新
|
489次组卷
|
19卷引用:山东省百所名校2020-2021学年上学期高三上学期12月联考数学试题
山东省百所名校2020-2021学年上学期高三上学期12月联考数学试题江苏省百校联考2020-2021学年高三上学期第二次考试数学试题重庆市2020-2021学年高三上学期12月诊断性考试数学试题山东省部分重点中学2021届高三上学期数学第二次质量检测试题江苏省扬州市高邮市临泽中学2021-2022学年高三下学期7月末阶段性测试数学试题江苏省无锡市江阴市青阳中学2020-2021学年高三上学期第二次段考数学试题江苏省常州市前黄高级中学2021-2022学年高三上学期10月学情检测数学试题山东省菏泽市定陶区第一中学2023-2024学年高二下学期第一次月考数学试题山东省烟台市第二中学2023-2024学年高二下学期6月月考数学试题江苏省无锡市梅村高级中学2020-2021学年高二上学期12月阶段检测数学试题(已下线)专题24 函数、不等式恒成立问题(测)-2021年高三数学二轮复习讲练测(新高考版)(已下线)数学-2021年高考考前20天终极冲刺攻略(一)(新高考地区专用)【学科网名师堂】 (5月19日)安徽省淮北市树人高级中学2023届高三下学期开学考试数学试题江苏省苏州吴江中学2023-2024学年高二下学期3月月考数学试题(已下线)专题2 三次函数问题(过关集训)江苏省南京市田家炳高级中学2020-2021学年高二下学期期初模拟检测数学试题(已下线)第五章 导数及其应用B卷(综合培优)-【双基双测】2021-2022学年高二数学同步单元AB卷(苏教版2019选择性必修第一册)江苏省南京市2023-2024学年高二上学期期末考前模拟数学试题安徽省十五校教育集团2023-2024学年高二上学期期末联考数学试题
名校
3 . 为了研究全年国内旅游人均消费情况与性别的关系,某互联网旅游公司从其网络平台数据库中抽取1000条用户信息进行调查,得到如下数据:
把全年旅游消费满16000元的游客称为“酷爱旅游者”.
(1)请完成下列2×2列联表,并判断能否在犯错误的概率不超过0.01的前提下,认为“酷爱旅游者”与性别有关;
(2)在庆祝公司成立15周年的系列活动中,董事会决定在其平台数据库的所有“酷爱旅游者”中随机抽取4名用户,担任网站的“形象大使”,每位“形象大使”可获得30000元奖金.另外,为了进一步刺激旅游消费,提升网站的知名度,公司将在其平台数据库的所有用户中抽取100名幸运用户给予现金奖励,规则如下:幸运用户在网页上点击“抽奖”按钮,屏幕上会随机显示两个数字,每个数字出现0~9的可能性是相等的.两个数字中,若同时有数字1和5,则获得一等奖,奖励1000元;若只有数字1和5中的一个,则获得二等奖,奖励500元;若数字1和5都没有,则获得三等奖,奖励200元.每位“酷爱旅游者”可进行两次抽奖;每位“非酷爱旅游者”可进行一次抽奖.
①视频率为概率,求抽取的4名“形象大使”中,既有男“酷爱旅游者”,又有女“酷爱旅游者”的概率;
②如果所有的“形象大使”和幸运用户都不放弃奖励,记移动支付平台支出的奖金总额为 ,求
,求 的数学期望.
的数学期望.
附:参考公式: ,其中
,其中 .
.
参考数据:
消费金额 (千元) (千元) | 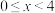 |  |  | 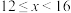 | 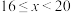 | 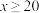 |
| 男(人数) | 105 | 80 | 67 | 48 | 44 | 56 |
| 女(人数) | 65 | 102 | 111 | 122 | 112 | 88 |
| 合计(人数) | 170 | 182 | 178 | 170 | 156 | 144 |
(1)请完成下列2×2列联表,并判断能否在犯错误的概率不超过0.01的前提下,认为“酷爱旅游者”与性别有关;
| 非酷爱旅游者 | 酷爱旅游者 | 合计 | |
| 男 | |||
| 女 | |||
| 合计 |
①视频率为概率,求抽取的4名“形象大使”中,既有男“酷爱旅游者”,又有女“酷爱旅游者”的概率;
②如果所有的“形象大使”和幸运用户都不放弃奖励,记移动支付平台支出的奖金总额为
 ,求
,求 的数学期望.
的数学期望.附:参考公式:
 ,其中
,其中 .
.参考数据:
  | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
2020-10-18更新
|
365次组卷
|
4卷引用:山东新高考质量测评联盟2020-2021学年高三上学期10月联考数学试题
山东新高考质量测评联盟2020-2021学年高三上学期10月联考数学试题湖南省岳阳市平江县第一中学2020-2021学年高三上学期11月月考数学试题江苏省无锡市大桥高中2020-2021学年高三上学期12月检测数学试题(已下线)专题19 概率与统计综合——2020年高考数学母题题源解密(山东、海南专版)
名校
解题方法
4 . 已知集合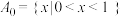 .给定一个函数
.给定一个函数 ,定义集合
,定义集合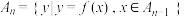 ,若
,若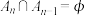 对任意的
对任意的 成立,则称该函数
成立,则称该函数 具有性质“
具有性质“ ”
”
(1)具有性质“ ”的一个一次函数的解析式可以是
”的一个一次函数的解析式可以是_________ ;
(2)给出下列函数:①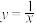 ;②
;②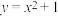 ;③
;③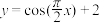 ,其中具有性质“
,其中具有性质“ ”的函数的序号是
”的函数的序号是_________ .
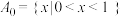 .给定一个函数
.给定一个函数 ,定义集合
,定义集合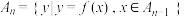 ,若
,若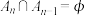 对任意的
对任意的 成立,则称该函数
成立,则称该函数 具有性质“
具有性质“ ”
”(1)具有性质“
 ”的一个一次函数的解析式可以是
”的一个一次函数的解析式可以是(2)给出下列函数:①
 ;②
;②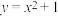 ;③
;③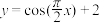 ,其中具有性质“
,其中具有性质“ ”的函数的序号是
”的函数的序号是
您最近一年使用:0次
2020-09-25更新
|
528次组卷
|
16卷引用:2020届山东省潍坊市高三2月数学模拟试题(一)
2020届山东省潍坊市高三2月数学模拟试题(一)2020届山东省寿光市第二中学高三线上2月29日数学高考模拟题(三)(已下线)备战2020年高考数学之考场再现(山东专版)06(已下线)强化卷04(3月)-冲刺2020高考数学之拿高分题目强化卷(山东专版)(已下线)第1篇——集合,常用逻辑用语-新高考山东专题汇编(已下线)第3篇——函数及其应用-新高考山东专题汇编【区级联考】北京市海淀区2019届高三年级第二学期期末练习(二模)数学理科试题(已下线)专题01 集合及其运算-冲刺2020高考跳出题海之高三数学模拟试题精中选萃江苏省南通市启东中学2020-2021学年高三上学期期初数学试题(已下线)专题01 集合(练)-2021年高考数学二轮复习讲练测(新高考版)(已下线)专题01 集合(练)-2021年高考数学二轮复习讲练测(文理通用)(已下线)专题02 常用逻辑用语-2022年高考数学一轮复习小题多维练(新高考版)陕西省咸阳市2022届高三下学期三模理科数学试题北京名校2023届高三二轮复习 专题三 集合与数列 第3讲 集合与数列创新题(已下线)专题01 条件开放型【练】【北京版】北京市八一学校2019~2020学年第二学期高一期中考试数学试题
名校
5 . 在流行病学中,基本传染数是指每名感染者平均可传染的人数.当基本传染数高于 时,每个感染者平均会感染一个以上的人,从而导致感染这种疾病的人数量指数级增长.当基本传染数持续低于
时,每个感染者平均会感染一个以上的人,从而导致感染这种疾病的人数量指数级增长.当基本传染数持续低于 时,疫情才可能逐渐消散.广泛接种疫苗可以减少疾病的基本传染数.假设某种传染病的基本传染数为
时,疫情才可能逐渐消散.广泛接种疫苗可以减少疾病的基本传染数.假设某种传染病的基本传染数为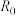 ,
, 个感染者在每个传染期会接触到
个感染者在每个传染期会接触到 个新人,这
个新人,这 人中有
人中有 个人接种过疫苗(
个人接种过疫苗(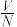 称为接种率),那么
称为接种率),那么 个感染者新的传染人数为
个感染者新的传染人数为 .已知新冠病毒在某地的基本传染数
.已知新冠病毒在某地的基本传染数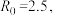 为了使
为了使 个感染者传染人数不超过
个感染者传染人数不超过 ,该地疫苗的接种率至少为( )
,该地疫苗的接种率至少为( )
 时,每个感染者平均会感染一个以上的人,从而导致感染这种疾病的人数量指数级增长.当基本传染数持续低于
时,每个感染者平均会感染一个以上的人,从而导致感染这种疾病的人数量指数级增长.当基本传染数持续低于 时,疫情才可能逐渐消散.广泛接种疫苗可以减少疾病的基本传染数.假设某种传染病的基本传染数为
时,疫情才可能逐渐消散.广泛接种疫苗可以减少疾病的基本传染数.假设某种传染病的基本传染数为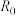 ,
, 个感染者在每个传染期会接触到
个感染者在每个传染期会接触到 个新人,这
个新人,这 人中有
人中有 个人接种过疫苗(
个人接种过疫苗(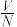 称为接种率),那么
称为接种率),那么 个感染者新的传染人数为
个感染者新的传染人数为 .已知新冠病毒在某地的基本传染数
.已知新冠病毒在某地的基本传染数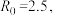 为了使
为了使 个感染者传染人数不超过
个感染者传染人数不超过 ,该地疫苗的接种率至少为( )
,该地疫苗的接种率至少为( )A. | B.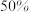 | C.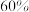 | D.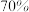 |
您最近一年使用:0次
2021-04-06更新
|
2129次组卷
|
12卷引用:山东省枣庄市第三中学2021-2022学年高三上学期第一次月考数学试题
山东省枣庄市第三中学2021-2022学年高三上学期第一次月考数学试题湖北省武汉市第二中学2021-2022学年高三上学期暑期模拟数学试题广东省广州市执信中学2022届高三上学期9月月考数学试题重庆市清华中学2022届高三上学期10月月考数学试题浙江省杭州市桐庐中学2022-2023学年新高三暑期阶段性测试数学试题山东省临沂市沂水县第四中学2022-2023学年高一上学期11月月考数学试题江苏省南京市、盐城市2021届高三下学期3月第二次模拟考试数学试题全国Ⅱ卷决胜高考2021届高三数学(理)仿真卷试题(三)广东省2022届高三上学期调研仿真数学试题(已下线)专题02 不等关系浙江省宁波市2021-2022学年高一上学期期末数学试题湖南省益阳市六校2022-2023学年高一上学期期末联考数学试题
名校
6 . 某快餐连锁店招聘外卖骑手,该快餐连锁店外卖覆盖A,B两个区域,骑手入职只能选择其中一个区域.其中区域A无底薪,外卖业务每完成一单提成5元;区域B规定每日底薪150元,外卖业务的前35单没有提成,从第36单开始,每完成一单提成8元.为激励员工,快餐连锁店还规定,凡当日外卖业务超过55单的外卖骑手可额外获得“精英骑手”奖励50元.该快餐连锁店记录了骑手每天的人均业务量,整理得到如图所示的两个区域外卖业务量的频率分布直方图.
(i)随机抽取一名骑手,求该骑手获得当日“精英骑手”奖励的概率;
(ii)若新入职的甲,乙、丙三名骑手分别到该快餐连锁店应聘,三人区域选择相互独立,求至少有两名骑手选择区域A的概率;
(2)若仅从人均日收入的角度考虑,新聘骑手应选择入职哪一区域?请说明你的理由(同组中的每个数据用该组区间的中点值代替).

(i)随机抽取一名骑手,求该骑手获得当日“精英骑手”奖励的概率;
(ii)若新入职的甲,乙、丙三名骑手分别到该快餐连锁店应聘,三人区域选择相互独立,求至少有两名骑手选择区域A的概率;
(2)若仅从人均日收入的角度考虑,新聘骑手应选择入职哪一区域?请说明你的理由(同组中的每个数据用该组区间的中点值代替).
您最近一年使用:0次
2021-10-27更新
|
786次组卷
|
6卷引用:山东省潍坊安丘市等三县2021-2022学年高三上学期10月过程性测试数学试题
名校
解题方法
7 . 已知函数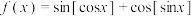 ,其中
,其中 表示不超过实数x的最大整数,关于
表示不超过实数x的最大整数,关于 有下述四个结论,正确的是( )
有下述四个结论,正确的是( )
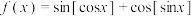 ,其中
,其中 表示不超过实数x的最大整数,关于
表示不超过实数x的最大整数,关于 有下述四个结论,正确的是( )
有下述四个结论,正确的是( )A. 的一个周期是 的一个周期是 | B. 是非奇非偶函数 是非奇非偶函数 |
C. 在 在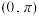 单调递减 单调递减 | D. 的最大值大于 的最大值大于 |
您最近一年使用:0次
2020-07-04更新
|
1802次组卷
|
8卷引用:山东省日照五莲县丶潍坊安丘市、潍坊诸城市、临沂兰山区2020届高三6月模拟数学试题
山东省日照五莲县丶潍坊安丘市、潍坊诸城市、临沂兰山区2020届高三6月模拟数学试题重庆市第一中学2021届高三上学期第一次月考数学试题(已下线)热点04 三角函数与解三角形-2021年高考数学【热点·重点·难点】专练(山东专用)江苏省淮安市涟水中学2020-2021学年高三上学期阶段检测(二)数学试题河北省衡水中学2022届高三上学期六调数学试题(已下线)2021届高三数学新高考“8+4+4”小题狂练(26)河北衡水中学2021届高三三轮复习自主复习旗开得胜数学(二)试题安徽省舒城中学2023届仿真模拟卷(一)数学试题
2020高三·山东·专题练习
名校
8 . 某专业机械生产厂为甲乙两地(两地仅气候条件差异较大,其他条件相同)的两个不同机器生产厂配套生产同一种零件,在甲乙两地分别任意选取100个零件进行抗疲劳破坏性试验,统计每个零件的抗疲劳次数(抗疲劳次数是指从开始试验到零件磨损至无法正常使用时的循环加载次数),将甲乙两地的试验的结果,即每个零件的抗疲劳次数(单位:万次)分别按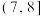 ,
,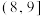 ,
,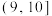 ,
,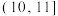 ,
, 分组进行统计,甲地的实验结果整理为如下的频率分布直方图(其中
分组进行统计,甲地的实验结果整理为如下的频率分布直方图(其中 ,
, ,
, 成等差数列,且
成等差数列,且 ),乙地的统计结果整理为如下的频数分布表.
),乙地的统计结果整理为如下的频数分布表.
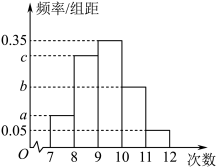
(1)求 ,
, ,
, 的值并计算甲地实验结果的平均数
的值并计算甲地实验结果的平均数 .
.
(2)如果零件抗疲劳次数超过9万次,则认为零件质量优秀,完成下列的 列联表:
列联表:
试根据上面完成的 列联表,通过计算分析判断,能否有97.5%的把握认为零件质量优秀与否与气候条件有关?
列联表,通过计算分析判断,能否有97.5%的把握认为零件质量优秀与否与气候条件有关?
附:临界值表
其中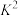 的观测值
的观测值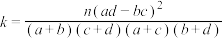
(3)如果将抗疲劳次数超过10万次的零件称为特优件,在甲地实验条件下,以频率为概率,随机打开一个4个装的零件包装箱,记其中特优件的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
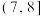 ,
,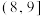 ,
,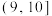 ,
,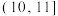 ,
, 分组进行统计,甲地的实验结果整理为如下的频率分布直方图(其中
分组进行统计,甲地的实验结果整理为如下的频率分布直方图(其中 ,
, ,
, 成等差数列,且
成等差数列,且 ),乙地的统计结果整理为如下的频数分布表.
),乙地的统计结果整理为如下的频数分布表.
(1)求
 ,
, ,
, 的值并计算甲地实验结果的平均数
的值并计算甲地实验结果的平均数 .
.(2)如果零件抗疲劳次数超过9万次,则认为零件质量优秀,完成下列的
 列联表:
列联表:质量不优秀 | 质量优秀 | 总计 | |
甲地 | |||
乙地 | |||
总计 |
试根据上面完成的
 列联表,通过计算分析判断,能否有97.5%的把握认为零件质量优秀与否与气候条件有关?
列联表,通过计算分析判断,能否有97.5%的把握认为零件质量优秀与否与气候条件有关?附:临界值表
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
其中
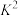 的观测值
的观测值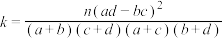
(3)如果将抗疲劳次数超过10万次的零件称为特优件,在甲地实验条件下,以频率为概率,随机打开一个4个装的零件包装箱,记其中特优件的个数为
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
您最近一年使用:0次
2020-05-15更新
|
184次组卷
|
3卷引用:2020届山东省青岛市高三5月模拟检测数学试题