名校
1 . 任取一个正整数,若是奇数,就将该数乘3再加上1;若是偶数,就将该数除以2.反复进行上述两种运算,经过有限次步骤后,必进入循环图 ,这就是数学史上著名的“冰霓猜想”(又称“角谷猜想”等).已知数列
,这就是数学史上著名的“冰霓猜想”(又称“角谷猜想”等).已知数列 满足:
满足: ,
,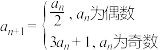 ,则
,则 ( )
( )
 ,这就是数学史上著名的“冰霓猜想”(又称“角谷猜想”等).已知数列
,这就是数学史上著名的“冰霓猜想”(又称“角谷猜想”等).已知数列 满足:
满足: ,
,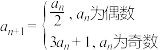 ,则
,则 ( )
( )| A.1 | B.2 | C.3 | D.4 |
您最近一年使用:0次
名校
解题方法
2 . 我国南宋时期杰出的数学家秦九韶在《数书九章》中提出了“三斜求积术”,其内容为:“以小斜幂,并大斜幂,减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂,减上,余四约之,为实;一为从隅,开平方得积.”把以上文字写成公式,即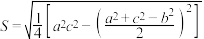 (其中S为面积,a,b,c为
(其中S为面积,a,b,c为 的三个内角A,B,C所对的边).若
的三个内角A,B,C所对的边).若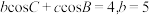 ,且
,且 ,则利用“三斜求积”公式可得
,则利用“三斜求积”公式可得 的面积
的面积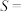 ( )
( )
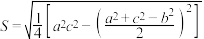 (其中S为面积,a,b,c为
(其中S为面积,a,b,c为 的三个内角A,B,C所对的边).若
的三个内角A,B,C所对的边).若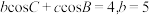 ,且
,且 ,则利用“三斜求积”公式可得
,则利用“三斜求积”公式可得 的面积
的面积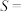 ( )
( )A. | B. | C. | D. |
您最近一年使用:0次
2024-04-01更新
|
1153次组卷
|
11卷引用:四川省南充高级中学2023-2024学年高一下学期第二次月考(5月)数学试卷
四川省南充高级中学2023-2024学年高一下学期第二次月考(5月)数学试卷山东省菏泽市第一中学八一路校区2023-2024学年高一下学期第三次月考数学试题陕西省渭南市三贤中学2023-2024学年高三下学期名校学术联盟高考模拟信息卷押题卷文科数学试题(二)(已下线)6.4.3.2?正弦定理15种常考题型归类(2)-高频考点通关与解题策略(人教A版2019必修第二册)(已下线)6.4.3.2 正弦定理——课后作业(基础版)(已下线)数学(全国卷文科03)(已下线)情境5 弘扬传统文化(已下线)情境1 源于教材阅读材料命题广东省佛山市南海区石门中学2023-2024学年高一下学期5月期中考试数学试题陕西省安康市高新中学2024届高三模拟考试最后一卷理科数学试题陕西省安康市高新中学2024届高三模拟考试最后一卷文科数学试题
名校
3 . 阿基米德有这样一句流传很久的名言:“给我一个支点,我就能撬起整个地球!”这句话说的便是杠杆原理,即“动力×动力臂=阻力×阻力臂”.现有一商店使用两臂不等长的天平称黄金,一位顾客到店里购买 黄金,售货员先将
黄金,售货员先将 的砝码放在天平左盘中,取出
的砝码放在天平左盘中,取出 黄金放在天平右盘中使天平平衡;再将
黄金放在天平右盘中使天平平衡;再将 的砝码放在天平右盘中,取
的砝码放在天平右盘中,取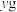 黄金放在天平左盘中使天平平衡,最后将称得的黄金交给顾客,则下列选项正确的是( )
黄金放在天平左盘中使天平平衡,最后将称得的黄金交给顾客,则下列选项正确的是( )
 黄金,售货员先将
黄金,售货员先将 的砝码放在天平左盘中,取出
的砝码放在天平左盘中,取出 黄金放在天平右盘中使天平平衡;再将
黄金放在天平右盘中使天平平衡;再将 的砝码放在天平右盘中,取
的砝码放在天平右盘中,取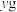 黄金放在天平左盘中使天平平衡,最后将称得的黄金交给顾客,则下列选项正确的是( )
黄金放在天平左盘中使天平平衡,最后将称得的黄金交给顾客,则下列选项正确的是( )A. | B.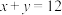 | C. | D.以上选项都有可能 |
您最近一年使用:0次
2024-03-31更新
|
234次组卷
|
2卷引用:四川省南充高级中学2023-2024学年高一下学期第一次月考(3月)数学试题
解题方法
4 . 在素数研究中,华裔数学家张益唐证明了孪生素数猜想的一个弱化形式,孪生素数是指相差为2的素数对,例如3和5,11和13等.从不超过10的正奇数中随机抽取2个,则这2个奇数是孪生素数的概率为( )
A. | B. | C. | D. |
您最近一年使用:0次
2024-03-13更新
|
348次组卷
|
5卷引用:四川省成都市教育科学研究院附属中学2023-2024学年高二下学期3月月考数学试题
四川省成都市教育科学研究院附属中学2023-2024学年高二下学期3月月考数学试题辽宁省名校联盟2023-2024学年高一下学期3月联合考试数学试题(已下线)15.2 随机事件的概率-【帮课堂】(苏教版2019必修第二册)(已下线)10.1.3 古典概型-同步精品课堂(人教A版2019必修第二册)(已下线)专题10.7 概率全章综合测试卷(基础篇)-举一反三系列(人教A版2019必修第二册)
名校
解题方法
5 . 中国古代著作《张丘建算经》中有这样一个问题:“今有马行转迟,次日减半疾,七日行七百里.”意思是说有一匹马行走的速度逐渐减慢,每天行走的里程是前一天的一半,七天一共行走了 里路,则该马第五天走的里程数约为( )
里路,则该马第五天走的里程数约为( )
 里路,则该马第五天走的里程数约为( )
里路,则该马第五天走的里程数约为( )A.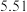 | B.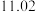 | C.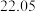 | D. |
您最近一年使用:0次
2024-03-13更新
|
551次组卷
|
4卷引用:四川省成都市玉林中学2023-2024学年高二下学期3月诊断性评价数学试题
2024高二·全国·专题练习
解题方法
6 . 意大利数学家列昂那多斐波那契以兔子繁殖为例,引入“兔子数列”:1,1,2,3,5,8,13,21,34,55, ,即
,即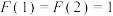 ,
,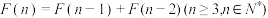 ,此数列在现代物理“准晶体结构”、化学等领域都有着广泛的应用.若此数列被2除后的余数构成一个新数列
,此数列在现代物理“准晶体结构”、化学等领域都有着广泛的应用.若此数列被2除后的余数构成一个新数列 ,则数列
,则数列 的前2024项的和为( )
的前2024项的和为( )
 ,即
,即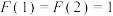 ,
,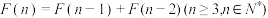 ,此数列在现代物理“准晶体结构”、化学等领域都有着广泛的应用.若此数列被2除后的余数构成一个新数列
,此数列在现代物理“准晶体结构”、化学等领域都有着广泛的应用.若此数列被2除后的余数构成一个新数列 ,则数列
,则数列 的前2024项的和为( )
的前2024项的和为( )| A.1348 | B.675 | C.1349 | D.1350 |
您最近一年使用:0次
2024-03-09更新
|
232次组卷
|
4卷引用:四川省达州外国语学校2023-2024学年高二下学期3月月考数学试题
四川省达州外国语学校2023-2024学年高二下学期3月月考数学试题广西''贵百河“2023-2024学年高二下学期4月新高考月考测试数学试卷(已下线)1.5 数学归纳法7种常见考法归类(2)(已下线)模块五 专题5 全真拔高模拟5(北师大高二期中)
名校
7 . 纯电动汽车是以车载电源为动力,用电机驱动车轮行驶,符合道路交通、安全法规各项要求的车辆,它使用存储在电池中的电来发动.因其对环境影响较小,逐渐成为当今世界的乘用车的发展方向.研究发现电池的容量随放电电流的大小而改变,1898年Peukert提出铅酸电池的容量 、放电时间
、放电时间 和放电电流
和放电电流 之间关系的经验公式:
之间关系的经验公式: ,其中
,其中 为与蓄电池结构有关的常数(称为Peukert常数),在电池容量不变的条件下,当放电电流为
为与蓄电池结构有关的常数(称为Peukert常数),在电池容量不变的条件下,当放电电流为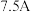 时,放电时间为
时,放电时间为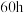 ;当放电电流为
;当放电电流为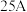 时,放电时间为
时,放电时间为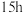 ,则该蓄电池的Peukert常数
,则该蓄电池的Peukert常数 约为(参考数据:
约为(参考数据: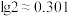 ,
,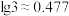 )( )
)( )
 、放电时间
、放电时间 和放电电流
和放电电流 之间关系的经验公式:
之间关系的经验公式: ,其中
,其中 为与蓄电池结构有关的常数(称为Peukert常数),在电池容量不变的条件下,当放电电流为
为与蓄电池结构有关的常数(称为Peukert常数),在电池容量不变的条件下,当放电电流为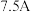 时,放电时间为
时,放电时间为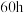 ;当放电电流为
;当放电电流为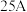 时,放电时间为
时,放电时间为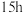 ,则该蓄电池的Peukert常数
,则该蓄电池的Peukert常数 约为(参考数据:
约为(参考数据: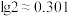 ,
,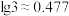 )( )
)( )| A.1.12 | B.1.13 |
| C.1.14 | D.1.15 |
您最近一年使用:0次
2024-03-01更新
|
1420次组卷
|
5卷引用:四川省德阳市第五中学2023-2024学年高二下学期4月月考数学试题
四川省德阳市第五中学2023-2024学年高二下学期4月月考数学试题四川省南充高中2023-2024学年高三下学期第十六次月考理科数学贵州省贵阳市第一中学2024届高三下学期一模考试数学试题(已下线)数学(全国卷理科01)(已下线)专题06 一轮复习指数函数,对数函数,幂函数--高二期末考点大串讲(人教A版2019)
8 . 在《增删算法统宗》中有如下问题:“三百七十八里关,初行健步不为难:次日脚痛减一半,六朝才得到其关”,其意思是:“某人到某地需走的路程为378里,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天才到达目的地”,则此人( )
A.第二天走的路程占全程的 |
| B.第三天走的路程为24里 |
| C.第一天走的路程比第四天走的路程多144里 |
| D.第五天和第六天共走路程18里 |
您最近一年使用:0次
2024-02-12更新
|
323次组卷
|
4卷引用:四川省成都市成华区嘉祥外国语高级中学高2023-2024学年高二下学期3月月考数学试题
四川省成都市成华区嘉祥外国语高级中学高2023-2024学年高二下学期3月月考数学试题四川省泸州市2023-2024学年高二上期期末统一考试数学试卷(已下线)5.3.2 等比数列的前n项和(3知识点+8题型+强化训练)-【帮课堂】2023-2024学年高二数学同步学与练(人教B版2019选择性必修第三册)(已下线)4.3.2 等比数列的前n项和公式——课堂例题
9 . 数学家也有许多美丽的错误,如法国数学家费马于1640年提出了以下猜想: 是质数.直到1732年才被善于计算的大数学家欧拉算出
是质数.直到1732年才被善于计算的大数学家欧拉算出 ,不是质数.现设
,不是质数.现设 ,数列
,数列 的前
的前 项和为
项和为 ,则使不等式
,则使不等式 成立的正整数
成立的正整数 的最大值为( )
的最大值为( )
 是质数.直到1732年才被善于计算的大数学家欧拉算出
是质数.直到1732年才被善于计算的大数学家欧拉算出 ,不是质数.现设
,不是质数.现设 ,数列
,数列 的前
的前 项和为
项和为 ,则使不等式
,则使不等式 成立的正整数
成立的正整数 的最大值为( )
的最大值为( )| A.11 | B.10 | C.9 | D.8 |
您最近一年使用:0次
2024-02-08更新
|
989次组卷
|
7卷引用:四川省成都市第十二中学2023-2024学年高二下学期3月月考数学试题
四川省成都市第十二中学2023-2024学年高二下学期3月月考数学试题重庆市七校联盟2024届高三下学期第一次月考数学试题山东省德州市第一中学2023-2024学年高二下学期3月月考数学试题山东省德州市夏津县第一中学2023-2024学年高二下学期3月月考数学试题陕西省咸阳市2024届高三上学期模拟检测(一)文科数学试题(已下线)第4讲:数列中的最值问题【练】(已下线)思想02 运用数形结合的思想方法解题(4大核心考点)(讲义)
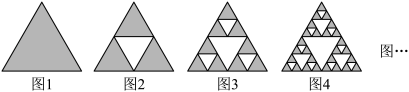
10 . 谢尔宾斯基三角形(Sierppinskitriangle)是一种分形,由波兰数学家谢尔宾斯基在1915年提出.先取一个实心正三角形,挖去一个“中心三角形”(即以原三角形各边的中点为顶点的三角形,即图中的白色三角形),然后在剩下的每个小三角形中又挖去一个“中心三角形”,用上面的方法可以无限操作下去.操作第1次得到图2,操作第2次得到图3.....,若继续这样操作下去后得到图2024,则从图2024中挖去的白色三角形个数是( )
A. | B.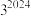 |
C.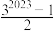 | D.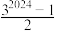 |
您最近一年使用:0次
2024-02-04更新
|
624次组卷
|
5卷引用:四川省成都市新津区成外学校2023-2024学年高二下学期3月月考数学试题



